Многогранники - это многомерные фигуры, которые имеют грани в виде плоскостей и вершины. Они широко используются в математике, графике, компьютерной графике, а также в других областях науки и техники. Для того чтобы правильно построить модель многогранника, необходимо ознакомиться с некоторыми методами и принципами, которые позволяют визуализировать и анализировать многогранники с высокой точностью и эффективностью.
Первый метод - это определение геометрических характеристик многогранника, таких как размеры сторон и углы между гранями. Зная эти характеристики, можно построить форму многогранника и сделать предварительное представление его внешнего вида. Кроме того, необходимо учесть особенности геометрической структуры многогранника, например, симметрию и наличие осей вращения.
Второй метод - это использование математической модели для описания многогранника. Такая модель может быть построена с помощью уравнений или неравенств, которые описывают грани и вершины многогранника. Кроме того, можно использовать векторное представление многогранника, которое позволяет легко выполнять различные операции, например, вычисление объема или площади поверхности.
Третий метод - это алгоритмическое построение модели многогранника. Существуют различные алгоритмы, которые позволяют автоматически генерировать модели многогранников различной сложности. Такие алгоритмы могут быть основаны на простых геометрических операциях, например, объединении и пересечении граней, или на сложных математических методах, таких как симплициальное разбиение. Важно выбрать подходящий алгоритм в зависимости от требуемой точности и эффективности моделирования.
Важность моделирования в науке

Модели многогранников - это один из видов моделей, используемых в математике и геометрии. Они позволяют наглядно представлять геометрические объекты и рассчитывать их характеристики. Модели многогранников находят применение в различных областях науки, включая физику, химию, биологию и информатику.
Использование моделей многогранников позволяет ученым более глубоко понять структуру и свойства объектов, а также предсказывать и анализировать их поведение в различных условиях. Благодаря моделированию многогранников, исследователи могут создавать и тестировать гипотезы, проверять различные возможные варианты и предсказывать результаты экспериментов.
Кроме того, моделирование многогранников позволяет визуализировать сложные математические концепции и абстрактные идеи, делая их более понятными и доступными для обучения и исследования. Это особенно важно для студентов и ученых, которые могут использовать модели многогранников для изучения геометрии, алгебры и других математических дисциплин.
Классификация многогранников
| Количество измерений | Название многогранника |
|---|---|
| 0D | Точка |
| 1D | Отрезок |
| 2D | Многоугольник |
| 3D | Многогранник |
| 4D | 4-мерный многогранник |
| ... | ... |
Кроме того, многогранники могут быть выпуклыми или невыпуклыми. Выпуклые многогранники имеют все вершины, лежащие внутри выпуклой оболочки, в то время как невыпуклые многогранники имеют хотя бы одну вершину вне выпуклой оболочки.
Одной из важных классификаций многогранников является классификация по типу граничных граней. Граничные грани многогранника могут быть треугольниками, квадратами, пятиугольниками и т.д., в зависимости от количества вершин.
Также многогранники можно классифицировать по своей топологической структуре. Например, простые многогранники - это многогранники, у которых все грани являются полигонами, а каждая ребра смежна ровно с двумя гранями. Сложные многогранники имеют более сложную топологическую структуру.
Таким образом, классификация многогранников представляет собой важный аспект изучения их свойств и структуры. Это помогает в анализе и построении моделей многогранников в различных приложениях и областях науки.
Методы построения моделей многогранников
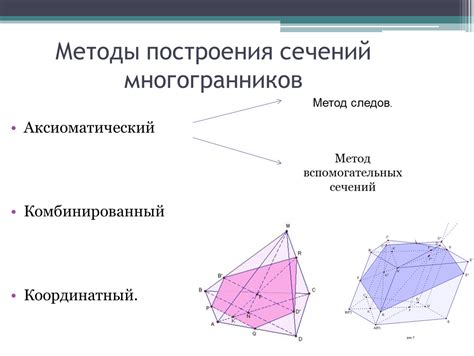
Одним из наиболее распространенных методов является метод конструктивных операций. Он основан на использовании простейших геометрических примитивов, таких как точки, отрезки, плоскости и полигоны, для создания сложных многогранников. Этот метод позволяет пошагово строить модель многогранника, добавляя или удаляя его элементы.
Еще одним методом является метод секущих плоскостей. Он основан на использовании пересечения плоскостей с многогранником. Путем изменения углов и положения плоскостей можно получить различные модели многогранников. Кроме того, этот метод позволяет определить геометрические свойства многогранника, такие как его объем, площадь поверхности и углы.
Также широко применяется метод случайных моделей. Он основан на генерации случайных точек и их последующем соединении, чтобы получить модель многогранника. Этот метод позволяет быстро создавать множество различных моделей многогранников и исследовать их свойства.
Необходимо отметить, что для построения моделей многогранников можно использовать различные программные инструменты. От простых графических редакторов до специализированных программных пакетов для трехмерного моделирования, эти инструменты помогают упростить процесс создания и визуализации моделей.
Весьма полезно ознакомиться и использовать все эти методы при работе с моделями многогранников, так как каждый из них имеет свои особенности и может быть эффективным в определенных ситуациях. Используя эти методы, можно создавать сложные и точные модели многогранников, которые могут использоваться в различных областях, таких как архитектура, наука, компьютерная графика и т.д.
Метод вершин
В данном методе сначала выбираются вершины многогранника, которые находятся на наибольших расстояниях от начала координат. Затем проводятся соответствующие отрезки, соединяющие выбранные вершины. Таким образом, получается граничная оболочка многогранника.
Далее, используя полученную граничную оболочку, можно построить полноценную модель многогранника. Для этого применяются различные алгоритмы и методы, такие как разбиение на грани и раскраска.
Метод вершин обладает рядом преимуществ. Во-первых, он достаточно прост в реализации и позволяет быстро получить модель многогранника. Во-вторых, он позволяет с высокой точностью воссоздать форму многогранника, особенно для многогранников с острой геометрической формой. Кроме того, метод вершин позволяет легко варьировать количество вершин, используемых в построении, что дает возможность получить различные варианты моделей многогранников.
Таким образом, метод вершин является важным инструментом в построении моделей многогранников и широко применяется в различных областях, таких как компьютерная графика, геометрия, архитектура и дизайн.
Метод граней
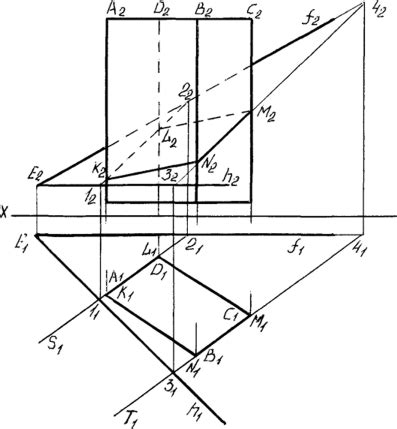
Данный метод имеет следующие принципы:
- Определение граней. Сначала необходимо определить грани многогранника. Для этого можно использовать различные алгоритмы, например, алгоритм поиска выпуклой оболочки или алгоритм построения диаграммы Вороного. Грани могут быть треугольниками, четырехугольниками или более сложными полигонами.
- Анализ граней. После определения граней необходимо проанализировать их свойства, такие как форма, ориентация, площадь, периметр и др. Эти характеристики граней могут быть использованы для классификации многогранников и извлечения информации о их структуре.
- Построение модели. Используя информацию об анализе граней, можно построить модель многогранника. Модель может быть представлена в виде сетки (меша) из вершин и граней, которые соединены друг с другом. Эта модель может быть использована для визуализации многогранника и проведения различных вычислений и операций над ним.
Метод граней имеет широкое применение в компьютерной графике, компьютерном зрении, геометрическом моделировании и других областях. Он позволяет эффективно работать с многогранниками различной сложности и формы, а также анализировать их структуру и свойства.
Метод ребер

Суть метода заключается в том, что каждое ребро многогранника представляет собой отдельный элемент модели. При построении модели многогранника на основе метода ребер необходимо задать координаты конечных точек каждого ребра, а также определить их взаимное расположение.
Основным преимуществом метода ребер является его простота и гибкость. Он позволяет строить модели многогранников различной сложности и формы. Благодаря использованию информации о ребрах, метод ребер позволяет получить более точные и детализированные модели, чем другие методы, такие как методы вершин или граней.
Однако метод ребер имеет и некоторые ограничения. Во-первых, он требует большего объема вычислений и может быть более трудоемким по сравнению с другими методами. Во-вторых, при построении модели многогранника на основе метода ребер необходимо обеспечить правильное соединение ребер, чтобы получить реалистичную и согласованную модель.
Итак, метод ребер является одним из важных способов построения модели многогранника. Он обладает преимуществами в виде простоты и гибкости, но имеет и некоторые ограничения. Однако, при правильном применении метод ребер может использоваться для создания реалистичных и детализированных моделей многогранников различной сложности и формы.
Принципы построения моделей многогранников
- Выбор подходящей системы координат: при построении модели многогранника важно правильно выбрать систему координат, которая будет соответствовать конкретным параметрам и особенностям объекта. Это позволяет удобно и точно определить положение и размеры многогранника.
- Определение граней и их свойств: каждый многогранник состоит из граней, их вершин и ребер. При построении модели необходимо точно определить все грани и описать их свойства, такие как площадь, форма и положение в пространстве. Это позволяет более точно и наглядно изобразить многогранник.
- Выбор подходящих методов и алгоритмов: в построении моделей многогранников применяются различные методы и алгоритмы, такие как геометрические преобразования, триангуляция и отсечение невидимых линий. Выбор подходящих методов и алгоритмов позволяет достичь более точных и реалистичных моделей.
- Использование понятного визуального языка: при построении модели многогранника необходимо использовать понятный и наглядный визуальный язык, который будет понятен любому пользователю. Для этого можно использовать различные элементы и символы, такие как линии, цвета и текстуры.
- Тестирование и проверка модели: перед окончательным представлением модели многогранника необходимо провести тестирование и проверку. Это позволяет обнаружить и исправить возможные ошибки, а также улучшить качество модели. Тестирование включает проверку внешнего вида, размеров, а также функциональности модели.
Соблюдение этих принципов позволяет создавать качественные и наглядные модели многогранников, которые могут быть использованы в различных областях, таких как архитектура, строительство, дизайн и наука.
Принцип декомпозиции
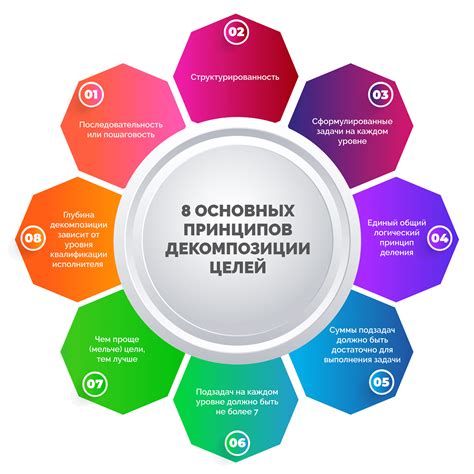
Декомпозиция помогает сделать модель более понятной и управляемой, а также улучшить ее структуру и обеспечить более эффективное решение задачи.
Принцип декомпозиции включает в себя следующие этапы:
- Разделение задачи на подзадачи. Это делается путем анализа требований и определения основных компонентов модели.
- Определение взаимодействия между подзадачами. На этом этапе определяются связи и зависимости между разными компонентами модели.
- Разработка детализации для каждой подзадачи. Здесь определяются все необходимые детали и параметры для решения каждой подзадачи.
- Интеграция всех компонентов модели в единую структуру. На этом этапе происходит сборка и объединение всех разработанных компонентов в единую модель многогранника.
Принцип декомпозиции позволяет упростить разработку и поддержку модели многогранника, а также улучшить ее гибкость, масштабируемость и повторное использование.
Принцип гармонии

Этот принцип подразумевает, что все элементы многогранника должны быть пропорциональными и соответствовать определенным правилам и закономерностям. Все стороны и ребра должны быть гармоничными и согласованными, что создает единое и привлекательное визуальное впечатление.
Важно отметить, что принцип гармонии также заключается в равномерном распределении элементов многогранника по его поверхности. Это позволяет создать сбалансированную и гармоничную модель.
Применение принципа гармонии в построении модели многогранника помогает создать эстетически приятную форму, которая визуально привлекательна и удовлетворяет глаз.