Поиск суммы чисел от 1 до 1000 может быть задачей с элементами сложности. Однако, с соблюдением определенных правил и использованием правильных методов, это задание выполнимо для каждого.
Возможно, вам уже знаком метод с использованием ручного подсчета. Однако, это займет немало времени и потребует большого внимания, чтобы не допустить ошибки. Если вы ищете более эффективный и надежный метод, вам следует воспользоваться формулой для суммы арифметической прогрессии.
Формула для суммы арифметической прогрессии выглядит следующим образом:
S = (a1 + an) * n / 2,
где S - искомая сумма, a1 - первый элемент прогрессии, an - последний элемент прогрессии, n - количество элементов в прогрессии.
Применяя данную формулу к числам от 1 до 1000, мы получим:
S = (1 + 1000) * 1000 / 2 = 500500.
Таким образом, сумма чисел от 1 до 1000 равна 500500. Пользуясь этим методом, вы сможете легко и быстро найти сумму любого диапазона чисел без длительного ручного подсчета.
Методы и советы для нахождения суммы чисел от 1 до 1000
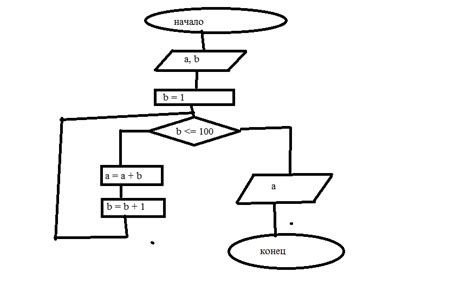
Нахождение суммы чисел от 1 до 1000 может быть выполнено различными способами. Вот несколько полезных методов и советов:
Использование формулы суммы арифметической прогрессии: Для нахождения суммы арифметической прогрессии можно использовать формулу S = (n/2)(a + b), где n - количество элементов, a - первый элемент, b - последний элемент. В данном случае, n = 1000, a = 1 и b = 1000. Подставив значения в формулу, получаем сумму: S = (1000/2)(1 + 1000) = 500 * 1001 = 500500.
Итеративный подсчет суммы: Другой способ - использование цикла для последовательного сложения всех чисел от 1 до 1000. Это можно сделать, используя язык программирования или просто с помощью калькулятора. Начиная с 1, при каждой итерации добавляем текущее число к накапливаемой сумме, и так продолжаем до 1000.
Геометрическое решение: Также мы можем рассмотреть решение с геометрической точки зрения. Можно применить мастерство разбиения последовательности, чтобы получить сумму. При том, что сумма чисел от 1 до 1000 слишком большая, можно разбить ее на несколько меньших сумм и затем сложить их все вместе. Например, мы можем разделить последовательность на группы по 100 чисел (1-100, 101-200 и т. д.) и посчитать сумму каждой группы. Затем сложим все эти суммы, чтобы получить итоговую.
Использование математических библиотек: В некоторых программных средах или языках программирования доступны математические библиотеки, которые содержат функции для быстрого вычисления суммы чисел или арифметических прогрессий. Использование таких библиотек может быть полезным и удобным способом для нахождения суммы чисел от 1 до 1000.
Выбор конкретного метода зависит от ваших предпочтений, уровня знаний и доступных ресурсов. Но в конечном итоге, все эти методы приведут к одному результату - сумме чисел от 1 до 1000, которая равна 500500.
Перебор чисел: простой и надежный способ

Введение:
Когда речь идет о нахождении суммы чисел от 1 до 1000, одним из самых простых и надежных способов является перебор чисел. Перебор - это базовая операция, при которой мы последовательно просматриваем все числа в заданном диапазоне и выполняем определенные действия с каждым числом.
Применение перебора:
Перебор чисел от 1 до 1000 позволяет нам найти сумму этих чисел, сложив их все вместе. Перебор является универсальным и простым подходом для решения различных задач, связанных с обработкой чисел.
Преимущества перебора:
Ниже приведены преимущества использования перебора для нахождения суммы чисел от 1 до 1000:
- Простота реализации: перебор не требует сложного математического аппарата или использования сложных алгоритмов. Достаточно просто перебрать все числа в заданном диапазоне и добавить их в сумму.
- Надежность: перебор является надежным способом нахождения суммы чисел, поскольку он последовательно обрабатывает каждое число в диапазоне и не допускает пропуска чисел или ненужных операций.
- Универсальность: перебор может быть использован для решения различных задач, связанных с обработкой чисел. Этот метод не привязан к конкретному диапазону чисел и может быть применен для любого набора чисел.
Пример кода:
Ниже приведен простой пример кода на языке Python, который демонстрирует использование перебора для нахождения суммы чисел от 1 до 1000:
# Инициализация суммы
sum_numbers = 0
# Перебор чисел от 1 до 1000
for i in range(1, 1001):
sum_numbers += i
print("Сумма чисел от 1 до 1000 равна:", sum_numbers)
Заключение:
Использование перебора является простым и надежным способом нахождения суммы чисел от 1 до 1000. Эта универсальная техника может быть применена для решения различных задач, связанных с обработкой чисел. Перебор позволяет последовательно обработать каждое число в заданном диапазоне и выполнить необходимые операции с этим числом.
Математическая формула: как вычислить сумму быстро и точно
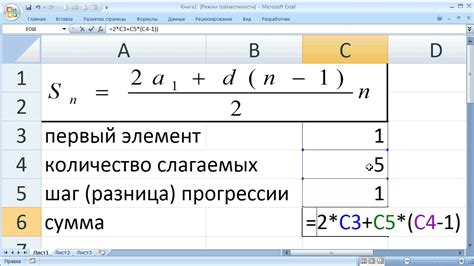
Вычисление суммы чисел от 1 до 1000 может быть затратным по времени задачей, если использовать обычный метод сложения каждого числа по очереди. Однако существует математическая формула, которая позволяет найти сумму такого ряда чисел быстро и точно.
Формула для вычисления суммы чисел от 1 до n:
S = n * (n + 1) / 2
Где S - сумма чисел, n - последнее число ряда (в данном случае 1000).
Применив данную формулу, мы можем быстро и безошибочно найти сумму чисел от 1 до 1000:
S = 1000 * (1000 + 1) / 2 = 1000 * 1001 / 2 = 500500
Таким образом, сумма чисел от 1 до 1000 равна 500500.
Использование математической формулы позволяет значительно сэкономить время и силы при вычислении подобных сумм, особенно если ряд чисел является большим.
Использование цикла: автоматическое сложение всех чисел

Процесс довольно прост. Мы начинаем с инициализации переменной, которая будет хранить текущую сумму. Затем мы создаем цикл, который будет выполняться 1000 раз - от 1 до 1000. Внутри цикла мы просто прибавляем текущее число к сумме. В конце цикла мы получаем сумму всех чисел.
Примерно так:
int sum = 0;
for (int i = 1; i <= 1000; i++) {
sum += i;
}
System.out.println("Сумма всех чисел от 1 до 1000: " + sum);
Таким образом, при выполнении данного кода мы получим результат - сумму всех чисел от 1 до 1000, которая равна 500500.
Использование цикла для автоматизации процесса сложения чисел позволяет нам значительно упростить и ускорить операции, которые требуют сложения большого количества чисел.
Рекурсивная функция: эффективный способ расчета суммы

Рекурсия - это вызов функцией самой себя. В данном случае, рекурсивная функция будет отвечать за суммирование чисел от 1 до N, где N - это число, переданное в качестве аргумента функции.
Преимущество рекурсивной функции заключается в ее простоте и понятности. Она позволяет за небольшое количество строк кода получить желаемый результат.
В нашем случае, для расчета суммы чисел от 1 до 1000, мы можем воспользоваться следующей рекурсивной функцией:
function sum(n) {
if (n === 1) {
return 1;
} else {
return n + sum(n - 1);
}
}
console.log(sum(1000));
В коде выше мы задаем функцию sum, которая принимает аргумент n. Если n равно 1, то функция возвращает 1. В противном случае, она вызывает себя же со значением n-1 и складывает n с результатом этого вызова.
В итоге, функция sum(1000) вернет нам сумму всех чисел от 1 до 1000, которая равна 500500.
Использование рекурсивной функции при расчете суммы чисел от 1 до 1000 позволяет получить результат эффективно и компактно. Однако, следует помнить, что рекурсия может быть ресурсоемкой операцией, так как каждый ее вызов занимает определенное количество памяти. Поэтому, при работе с большими значениями следует оценивать возможные ограничения и оптимизировать код при необходимости.
Применение арифметической прогрессии: сумма без сложения всех чисел

Для нахождения суммы всех чисел от 1 до 1000, можно воспользоваться формулой суммы арифметической прогрессии:
S = (n * (a + b)) / 2,
где:
- S – сумма всех чисел;
- n – количество элементов в прогрессии;
- a – первый элемент последовательности (в данном случае 1);
- b – последний элемент последовательности (в данном случае 1000).
Применяя эту формулу, можно получить сумму всех чисел от 1 до 1000 без необходимости сложения всех чисел по отдельности:
S = (1000 * (1 + 1000)) / 2 = 500500.
Таким образом, сумма всех чисел от 1 до 1000 равна 500500. Этот метод позволяет эффективно и быстро найти сумму большого количества чисел, применяя формулу арифметической прогрессии.
Использование библиотек: готовые инструменты для быстрого решения задачи
Вступление:
Поиск суммы чисел от 1 до 1000 является стандартной задачей, которую можно решить с помощью простого цикла. Однако, существуют готовые инструменты, такие как библиотеки, которые позволяют решить эту задачу гораздо быстрее и эффективнее. В данном разделе мы рассмотрим несколько библиотек, которые могут быть полезны при поиске суммы чисел.
1. NumPy:
NumPy - это библиотека для языка программирования Python, которая обеспечивает поддержку многомерных массивов и математических функций, работающих с этими массивами. Для нахождения суммы чисел от 1 до 1000 с использованием NumPy, можно воспользоваться функцией numpy.sum():
import numpy as np
numbers = np.arange(1, 1001)
sum_of_numbers = np.sum(numbers)
print(sum_of_numbers)
2. Pandas:
Pandas - это библиотека для языка программирования Python, предназначенная для обработки и анализа данных. С помощью Pandas можно легко находить сумму чисел, включая не только последовательности, но и данные из таблиц.
Приведенный ниже пример показывает, как можно найти сумму чисел от 1 до 1000 с помощью Pandas:
import pandas as pd
numbers = pd.Series(range(1, 1001))
sum_of_numbers = numbers.sum()
print(sum_of_numbers)
3. MATLAB:
MATLAB - это высокоуровневый язык программирования и среда разработки, позволяющая выполнять численные расчеты и визуализацию данных. С помощью MATLAB можно решать сложные задачи, включая нахождение сумм чисел.
В следующем примере показано, как можно использовать MATLAB для нахождения суммы чисел от 1 до 1000:
numbers = 1:1000;
sum_of_numbers = sum(numbers);
disp(sum_of_numbers);
Заключение:
Использование готовых библиотек и инструментов значительно упрощает решение задачи поиска суммы чисел от 1 до 1000. Библиотеки, такие как NumPy, Pandas и MATLAB, предоставляют мощные функциональные возможности для работы с числовыми данными и выполнения сложных вычислений. Используйте эти инструменты и экономьте время, получая результаты быстрее и эффективнее.
Оптимизация вычислений: как ускорить процесс нахождения суммы
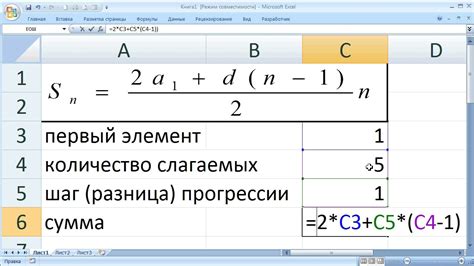
Нахождение суммы чисел от 1 до 1000 может занять приличное количество времени. Однако, существуют методы, которые позволяют оптимизировать этот процесс и значительно ускорить его выполнение. В данном разделе мы рассмотрим несколько таких методов.
Первым методом является использование формулы арифметической прогрессии. Если нужно найти сумму всех чисел от 1 до N, то можно воспользоваться формулой:
S = (N * (N + 1)) / 2
Эта формула позволяет вычислить сумму чисел от 1 до N за константное время, независимо от значения N.
Вторым методом является использование цикла с увеличением суммы на каждой итерации. В данном случае, мы начинаем с нулевой суммы и последовательно добавляем каждое число от 1 до N:
sum = 0 for i = 1 to N sum = sum + i next i
Хотя этот метод требует выполнения N итераций, он является достаточно эффективным и может быть использован для вычислений с относительно небольшими значениями N.
Третий метод основан на использовании битовых операций. Если N является степенью двойки, то можно использовать следующий алгоритм для вычисления суммы:
sum = 0 for i = 1 to log2(N) sum = sum + (N >> i) next i
Этот метод позволяет ускорить процесс вычисления суммы для чисел, которые являются степенями двойки.
В общем случае, для нахождения суммы чисел от 1 до 1000 рекомендуется использовать формулу арифметической прогрессии или цикл. Однако, для работы с более большими значениями N или специфическими числами, можно использовать и другие методы, учитывающие особенности задачи и позволяющие сэкономить время на вычислениях.
| Метод | Время выполнения |
|---|---|
| Формула арифметической прогрессии | Константное |
| Цикл | O(N) |
| Битовые операции (для степеней двойки) | log(N) |