Центр тяжести треугольника – особая точка, которая имеет большое значение в геометрии. Он располагается внутри треугольника и характеризует равномерное распределение массы треугольника. Поэтому для многих методов их прикладного использования необходимо знать положение центра тяжести.
Один из наиболее распространенных методов нахождения центра тяжести – метод средних перпендикуляров. Суть метода заключается в построении медиан треугольника – это отрезки, соединяющие вершины треугольника с серединами противоположных сторон. Центральная точка пересечения медиан и будет являться центром тяжести треугольника.
Если треугольник ABC задан координатами своих вершин (x1, y1), (x2, y2) и (x3, y3), то для нахождения центра тяжести можно воспользоваться формулой:
xg = (x1 + x2 + x3) / 3
yg = (y1 + y2 + y3) / 3
Другим известным методом нахождения центра тяжести является метод разделения треугольника на три подобных треугольника. При этом каждый из полученных треугольников имеет две общие вершины с исходным треугольником. Центр тяжести треугольника будет находиться на пересечении прямых, соединяющих вершины средних подобных треугольников.
Определение понятия "центр тяжести"
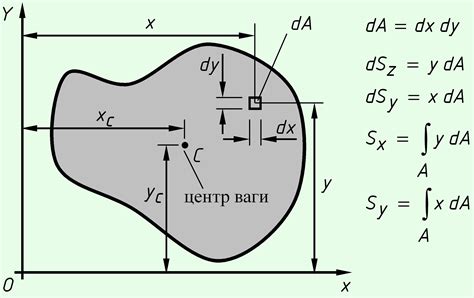
Центр тяжести играет важную роль в механике и статике, а также в различных физических и геометрических расчетах и приложениях.
Определение центра тяжести треугольника основывается на принципе, согласно которому каждая точка треугольника вносит свой вклад в общую силу тяжести, пропорциональный массе данной точки.
Центр тяжести треугольника может быть найден при помощи различных методов, включая метод векторов, метод координат и метод взвешивания треугольника.
Знание положения центра тяжести треугольника позволяет проводить рассчеты его равновесия, определять его устойчивость и предсказывать его поведение в различных физических процессах.
Способы расчета координат центра тяжести
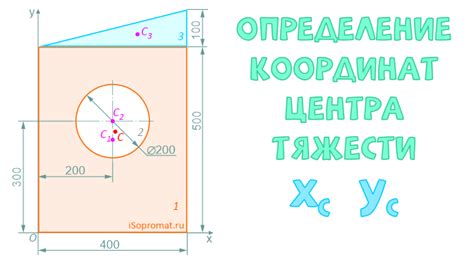
1. Метод средних координат: для расчета координат центра тяжести треугольника, необходимо найти средние значения координат вершин по каждой оси. То есть, суммировать значения координат вершин по каждой оси и разделить их на количество вершин. Полученные значения будут координатами центра тяжести.
2. Метод взвешивания: в данном методе каждая точка треугольника взвешивается по площади, которую она занимает в треугольнике. Затем, координаты центра тяжести вычисляются как средневзвешенные значения координат всех точек треугольника.
3. Метод суммирования медиан: в этом методе вычисляются суммы координат медиан треугольника. Затем, координаты центра тяжести вычисляются как суммы координат медиан, разделенные на число медиан.
Выбор метода расчета зависит от конкретной задачи и доступных данных о треугольнике.
Важно помнить, что центр тяжести является точкой пересечения медиан и имеет равные расстояния до каждой вершины треугольника.
Метод использования координат вершин треугольника
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Для нахождения центра тяжести треугольника, необходимо найти координаты середины каждой стороны и соединить их линиями.
Для треугольника с координатами вершин A(x1, y1), B(x2, y2) и C(x3, y3), координаты центра тяжести G(xg, yg) могут быть вычислены следующим образом:
- Найдите координаты середины стороны AB:
- xg = (x1 + x2) / 2
- yg = (y1 + y2) / 2
- xg = (x2 + x3) / 2
- yg = (y2 + y3) / 2
- xg = (x3 + x1) / 2
- yg = (y3 + y1) / 2
Точка G(xg, yg) будет являться центром тяжести треугольника ABC.
Метод использования площадей треугольников
Для нахождения центра тяжести треугольника можно использовать метод, основанный на площадях отдельных треугольников, образующих исходный треугольник.
Для этого сначала найдем середины сторон треугольника, соединяющие вершины с противоположными сторонами. Они разделят каждую сторону на две равные части. Полученные точки назовем точками пересечения медиан треугольника.
Затем проведем из вершин треугольника линии до соответствующих точек пересечения медиан. В результате мы получим шесть треугольников, каждый из которых можно рассматривать как отдельную фигуру.
Далее найдем площади каждого из полученных треугольников. Это можно сделать, используя различные формулы для расчета площади треугольника в зависимости от известных данных, таких как длины сторон и высоты.
После нахождения площадей треугольников можно найти их центры тяжести, используя координаты вершин каждого треугольника и известную площадь.
И наконец, для нахождения центра тяжести исходного треугольника можно усреднить координаты центров тяжести каждого из треугольников, взвешивая их на соответствующие площади. Полученные координаты будут координатами центра тяжести исходного треугольника.
Таким образом, метод использования площадей треугольников предоставляет возможность определить точное положение центра тяжести треугольника на плоскости.
Метод использования векторов
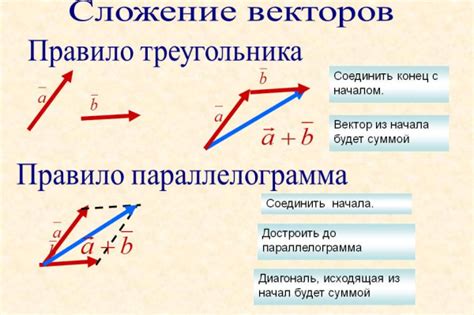
Для начала, рассмотрим, что представляет собой вектор. Вектор - это направленный отрезок, который имеет определенную длину и направление. Вектор можно задать двумя точками - начальной и конечной.
Для вычисления центра тяжести треугольника с помощью векторов, необходимо найти векторы, соединяющие вершины треугольника с его центром тяжести. Затем нужно найти сумму этих векторов и разделить ее на три, чтобы получить вектор центра тяжести.
Формула для нахождения центра тяжести треугольника с использованием векторов выглядит следующим образом:
G = (A + B + C) / 3
где G - вектор центра тяжести треугольника, A, B, C - векторы, соединяющие вершины треугольника с его центром тяжести.
Таким образом, метод использования векторов позволяет вычислить координаты центра тяжести треугольника, используя свойства и алгебраические операции с векторами.
Метод использования масс и расстояний
Для применения этого метода нужно знать массу каждой из вершин треугольника и расстояние от каждой вершины до центра тяжести. Центр тяжести треугольника можно найти, используя формулы:
1. Координата xцт центра тяжести:
xцт = (m1x1 + m2x2 + m3x3) / (m1 + m2 + m3),
где m1, m2, m3 – массы вершин треугольника, x1, x2, x3 – координаты вершин треугольника по оси x.
2. Координата yцт центра тяжести:
yцт = (m1y1 + m2y2 + m3y3) / (m1 + m2 + m3),
где m1, m2, m3 – массы вершин треугольника, y1, y2, y3 – координаты вершин треугольника по оси y.
Найдя значения xцт и yцт, можно определить координаты точки, в которой находится центр тяжести треугольника.
Метод использования свойств сил тяжести

Для применения данного метода необходимо знать, что сила тяжести действует на каждый отдельный элемент треугольника и обратно пропорциональна его массе.
Используя метод сил тяжести, мы можем определить положение центра тяжести треугольника следующим образом:
1. Разделить треугольник на три элемента.
Так как треугольник имеет три стороны и три угла, мы можем разделить его на три элемента: первый элемент - это одна из сторон треугольника, второй элемент - это вторая сторона, а третий элемент - это третья сторона.
2. Определить массу каждого элемента.
Масса каждого элемента треугольника зависит от его площади. Мы можем определить массу каждого элемента, используя формулу массы:
масса = площадь * плотность
3. Определить положение центра тяжести каждого элемента.
Положение центра тяжести каждого элемента можно определить, зная его форму и равномерное распределение массы внутри него. Для треугольника, центр тяжести каждого элемента находится на его серединной перпендикулярной линии.
4. Найти общий центр тяжести.
Общий центр тяжести треугольника является средним положением центров тяжести каждого элемента. Для этого необходимо сложить координаты каждого центра тяжести и разделить их на три.
Используя метод сил тяжести, мы можем точно определить положение центра тяжести треугольника. Этот метод является одним из самых точных способов вычисления центра тяжести и широко применяется в научных и инженерных расчетах.
Положение центра тяжести внутри треугольника
Если треугольник ABC имеет вершины A(x1, y1), B(x2, y2) и C(x3, y3), то координаты центра тяжести G можно найти по следующим формулам:
Gx = (x1 + x2 + x3) / 3
Gy = (y1 + y2 + y3) / 3
Таким образом, чтобы найти положение центра тяжести треугольника, необходимо сложить координаты вершин треугольника и разделить результат на 3.
Центр тяжести является важной характеристикой треугольника, поскольку определяет равновесие его массы. Он также является точкой, относительно которой треугольник сбалансирован, что позволяет использовать его в решении задач механики и физики.
Центр тяжести в центральной части треугольника
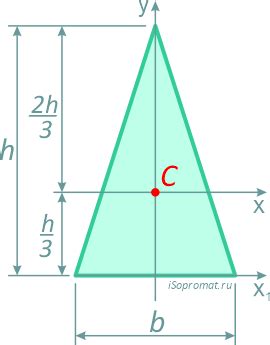
Центр тяжести является точкой баланса треугольника, так как он расположен в центре его массы. В этой точке сумма моментов сил относительно центра масс треугольника равна нулю. Это означает, что треугольник можно считать равнораспределенной массой.
Центр тяжести является важным понятием в механике и строительстве. Он помогает определить равновесие треугольников и предсказывать их поведение в различных условиях. Знание о положении центра тяжести треугольника может быть полезным при построении строений или при проведении различных расчетов в инженерных задачах.
Центр тяжести на серединных перпендикулярах сторон треугольника
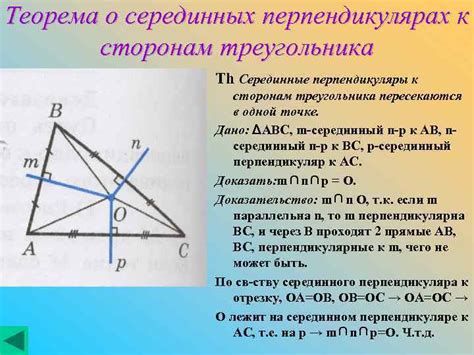
Серединный перпендикуляр - это прямая, которая проходит через середину стороны треугольника и перпендикулярна этой стороне. Для каждой стороны треугольника есть свой серединный перпендикуляр.
Если провести серединные перпендикуляры ко всем сторонам треугольника и их точки пересечения соединить, то получится точка, которая будет являться центром тяжести треугольника.
Математически это можно представить следующим образом:
1. Найдите середины сторон треугольника.
Получение середины стороны:
Середина стороны треугольника находится посередине между двумя концами этой стороны. Для нахождения середины стороны следует сложить координаты концов стороны и поделить полученную сумму на 2:
(x1 + x2) / 2, (y1 + y2) / 2
2. Постройте серединные перпендикуляры к сторонам треугольника.
Получение серединного перпендикуляра:
Серединный перпендикуляр к стороне треугольника проходит через середину этой стороны и перпендикулярен ей. Для построения серединного перпендикуляра следует определить его уравнение, зная координаты середины стороны и направляющего вектора стороны:
Уравнение перпендикуляра: (x - x0) * a + (y - y0) * b = 0,
где a и b - координаты направляющего вектора стороны, (x0, y0) - координаты середины стороны.
3. Найдите точку пересечения серединных перпендикуляров.
Получение точки пересечения серединных перпендикуляров:
Точка пересечения серединных перпендикуляров может быть найдена с помощью системы уравнений, состоящей из уравнений перпендикуляров.
Решив систему уравнений, полученных для каждой пары серединных перпендикуляров, получится точка, которая будет являться центром тяжести треугольника.
Таким образом, метод нахождения центра тяжести на серединных перпендикулярах сторон треугольника позволяет определить точку, в которой сосредоточена вся масса треугольника.
Центр тяжести на медианах треугольника

Чтобы найти центр тяжести на медианах, необходимо найти середины каждой стороны треугольника и соединить эти точки. Точка пересечения этих отрезков и будет являться центром тяжести.
Пример:
Дан треугольник ABC, где A(1,1), B(4,5) и C(7,2). Найдем центр тяжести треугольника:
Найдем координаты точки M1, являющейся серединой стороны BC. Для этого найдем среднее арифметическое координат x и y:
xM1 = (xB + xC) / 2 = (4 + 7) / 2 = 11 / 2 = 5.5
yM1 = (yB + yC) / 2 = (5 + 2) / 2 = 7 / 2 = 3.5
Таким образом, координаты точки M1 равны (5.5, 3.5).
Аналогично находим координаты точек M2 и M3 для сторон AC и AB:
xM2 = (xA + xC) / 2 = (1 + 7) / 2 = 8 / 2 = 4
yM2 = (yA + yC) / 2 = (1 + 2) / 2 = 3 / 2 = 1.5
Координаты точки M2 равны (4, 1.5).
xM3 = (xA + xB) / 2 = (1 + 4) / 2 = 5 / 2 = 2.5
yM3 = (yA + yB) / 2 = (1 + 5) / 2 = 6 / 2 = 3
Координаты точки M3 равны (2.5, 3).
Теперь соединим эти точки и найдем их точку пересечения:
Точка пересечения медиан имеет координаты (4, 2.33). Это и есть центр тяжести треугольника ABC.
Таким образом, мы нашли координаты центра тяжести треугольника на медианах: (4, 2.33).


