Треугольник - одна из основных фигур в геометрии, и его стороны и углы играют важную роль при решении различных задач. В числе треугольников особую роль играют прямоугольные треугольники, у которых один из углов равен 90 градусам. Одна из важных сторон прямоугольного треугольника - гипотенуза, которая является самой длинной стороной и соединяет два острых угла.
Одним из основных интересующих вопросов о прямоугольных треугольниках является нахождение длины гипотенузы. Узнав длину гипотенузы, можно решить множество задач, включая определение площади треугольника и нахождение длины других его сторон. Существует несколько методов нахождения отрезка гипотенузы, которые мы рассмотрим в данной статье.
Метод Пифагора - один из наиболее известных методов нахождения отрезка гипотенузы треугольника. Согласно теореме Пифагора, в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Этот метод основан на простой математической формуле и дает точный результат.
Пример: Предположим, что у нас есть прямоугольный треугольник, у которого один катет равен 3, а другой катет равен 4. С использованием метода Пифагора мы можем найти гипотенузу следующим образом: гипотенуза в квадрате равна сумме квадратов катетов (3^2 + 4^2), что равно 9 + 16, т.е. 25. Далее мы извлекаем квадратный корень из 25, что дает нам гипотенузу равной 5.
По теореме Пифагора
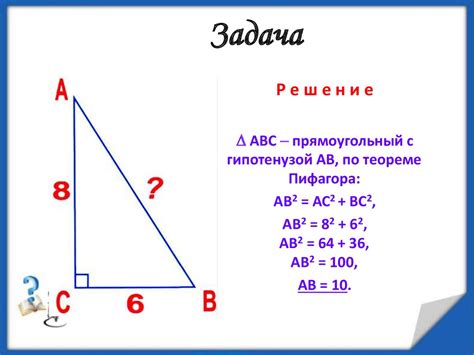
Метод нахождения отрезка гипотенузы треугольника по теореме Пифагора основан на знании длин двух его других сторон. Эта теорема гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Таким образом, если известна длина одного из катетов и длина гипотенузы, можно найти длину другого катета. Для этого необходимо использовать формулу:
a2 + b2 = c2
где a и b - длины катетов, а c - длина гипотенузы.
С помощью геометрических построений
Существует несколько методов нахождения отрезка гипотенузы треугольника с помощью геометрических построений. Один из таких методов основан на использовании перпендикуляра к гипотенузе.
Для начала построим треугольник ABC, где AB - гипотенуза. Затем проведем высоту CD, которая является перпендикуляром к гипотенузе AB.
Получившийся треугольник ACD будет прямоугольным, так как угол CAD является прямым углом. Теперь мы можем использовать известные длины сторон AD и AC для нахождения длины гипотенузы AB.
Воспользуемся теоремой Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Таким образом, получаем уравнение:
AB2 = AD2 + CD2
Раскроем скобки и получим:
AB2 = AD2 + BC2
Найдем известные длины сторон AD и BC с помощью геометрических построений или из условия задачи, и подставим их в уравнение. Зная длину AB, мы можем определить длину отрезка гипотенузы треугольника.
Приведем пример для наглядности. Предположим, что AD = 4 и BC = 5. Подставив эти значения в уравнение, получаем:
AB2 = 42 + 52
AB2 = 16 + 25
AB2 = 41
AB ≈ √41
Таким образом, длина отрезка гипотенузы треугольника примерно равна корню из 41.
Используя геометрические построения и теорему Пифагора, мы можем определить длину отрезка гипотенузы треугольника, зная длины сторон AD и BC.
С использованием тригонометрических функций

Другой метод нахождения отрезка гипотенузы треугольника основывается на использовании тригонометрических функций. Для этого необходимо знать длины двух других сторон треугольника или значения углов.
Если известны длины катетов треугольника, то можно использовать теорему Пифагора и формулу sin для нахождения отрезка гипотенузы. Формула имеет вид:
c = sqrt(a^2 + b^2)
где c - длина гипотенузы, a и b - длины катетов.
Если же известны значения углов треугольника, то можно использовать тригонометрические функции sin, cos или tan для нахождения длин сторон и отрезка гипотенузы. Например, если известны два угла треугольника и длина одной стороны, то можно использовать формулы:
a = c * sin(A)
b = c * sin(B)
где a и b - длины катетов, c - длина гипотенузы, A и B - углы треугольника.
Таким образом, с использованием тригонометрических функций можно легко находить отрезок гипотенузы треугольника, зная длины катетов или значения углов.
По прямым углам и высотам
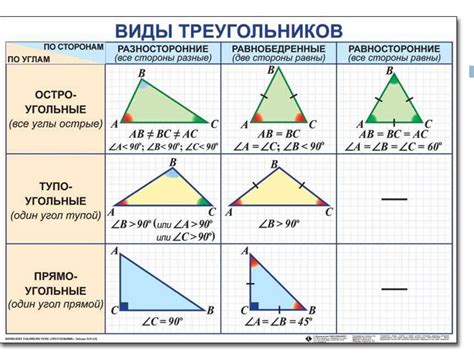
Прямой угол - это угол, равный 90 градусам, который образуется при пересечении двух прямых линий. В треугольнике угол, противолежащий гипотенузе, всегда является прямым углом. Это означает, что в прямоугольном треугольнике одна сторона всегда будет гипотенузой, а другие две стороны - катетами.
Высота треугольника - это отрезок, проведенный из вершины треугольника перпендикулярно к основанию, которое является одной из сторон треугольника. В прямоугольном треугольнике высота, проведенная из вершины прямого угла к основанию - это отрезок, который делит гипотенузу на две равные части.
С использованием свойств прямых углов и высот можно определить, что отрезок гипотенузы равен сумме произведений длин катетов. Другими словами, гипотенуза в прямоугольном треугольнике вычисляется по формуле: гипотенуза = √(катет1^2 + катет2^2).
Например, рассмотрим прямоугольный треугольник со сторонами a = 3 и b = 4. Применив формулу, мы можем найти гипотенузу c: c = √(3^2 + 4^2) = √(9 + 16) = √25 = 5. Таким образом, длина гипотенузы данного треугольника равна 5.
Метод нахождения отрезка гипотенузы треугольника по прямым углам и высотам является одним из базовых методов решения задач геометрии и может быть использован для нахождения длины гипотенузы в различных контекстах.
С применением векторов и скалярного произведения

Метод нахождения отрезка гипотенузы треугольника с помощью векторов и скалярного произведения основан на использовании свойств этих математических операций.
Для начала, вспомним, что вектор - это направленный отрезок, который имеет определенную длину и направление. Скалярное произведение двух векторов определяет произведение модулей этих векторов на косинус угла между ними.
В данном случае, мы рассматриваем треугольник с гипотенузой АС и катетами AB и BC. Мы хотим найти длину гипотенузы АС. Для этого мы можем использовать векторы AB и BC.
Сначала найдем вектор AB, который будет равен разности координат точек B и A:
AB = (xB - xA, yB - yA)
Аналогично, найдем вектор BC:
BC = (xC - xB, yC - yB)
Теперь найдем скалярное произведение векторов AB и BC:
(AB ⋅ BC) = (xA - xB)(xC - xB) + (yA - yB)(yC - yB)
Далее, найдем модуль этих векторов:
|AB| = √((xA - xB)^2 + (yA - yB)^2)
|BC| = √((xC - xB)^2 + (yC - yB)^2)
Наконец, найдем модуль гипотенузы АС по формуле:
|AC| = √(|AB|^2 + |BC|^2 - 2(AB ⋅ BC))
Таким образом, используя векторы и скалярное произведение, мы можем найти длину гипотенузы треугольника. Данный метод может быть полезен в случаях, когда известны координаты вершин треугольника и требуется найти его гипотенузу.