График функции – важный инструмент в математике, который позволяет наглядно представить зависимость между переменными. Определение прохождения графика функции является ключевой задачей при изучении функционального анализа. На этапе анализа графика необходимо понять, на каких участках график функции возрастает, убывает или остается постоянным. Это позволяет выявить максимумы и минимумы функции, а также найти те точки, где происходят разрывы, области значений функции и места экстремумов.
Существует несколько методов, позволяющих точно определить прохождение графика функции. Один из самых популярных методов - это метод производной. Для этого вычисляется производная функции, и затем анализируется ее знак на заданном интервале. Если производная положительна на каком-то интервале, то функция возрастает на этом интервале. Если производная отрицательна, то функция убывает. Если производная равна нулю, то функция достигает экстремальной точки.
Еще один метод - это построение таблицы знаков функции. Для этого берутся некоторые характерные точки на интервале, например, точки экстремумов или точки разрыва. А затем анализируется знак функции на каждом из этих интервалов. Если функция положительна на интервале, то график функции будет находиться выше оси абсцисс. Если функция отрицательна, то график будет находиться ниже оси абсцисс. Если функция равна нулю, то график будет пересекать ось абсцисс.
Математическое определение графика функции
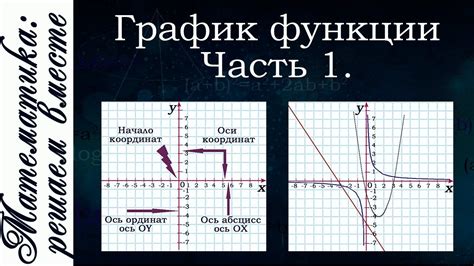
На графике функции можно наблюдать такие характеристики, как монотонность, точки экстремума, пересечения с осями, асимптоты и другие. Он позволяет визуализировать и анализировать поведение функции на всем ее области определения.
График функции может быть построен как вручную, с использованием геометрических инструментов, так и с помощью математических программ или специализированных графических редакторов. Он позволяет увидеть основные особенности и свойства функции, что облегчает понимание ее поведения и принятие решений на основе полученных данных.
Построение графика функции является важным инструментом для анализа и представления математических моделей, а также для исследования и предсказания различных явлений и процессов в естественных и общественных науках.
Аналитический подход к определению прохождения графика функции

Аналитический подход к определению прохождения графика функции позволяет определить точные значения, при которых график функции пересекает ось абсцисс или ось ординат.
Для определения прохождения графика функции через ось абсцисс необходимо решить уравнение функции относительно значения аргумента, при котором функция равна нулю. Найденное значение аргумента будет точкой, в которой график функции пересекает ось абсцисс.
Аналогично, для определения прохождения графика функции через ось ординат необходимо найти уравнение прямой, параллельной оси ординат и пересекающей график функции. Затем решив данное уравнение, можно определить точку пересечения графика функции с осью ординат.
Аналитический подход позволяет получить точные значения и координаты точек прохождения графика функции через оси. Такой подход особенно полезен, когда требуется точность и представление графика функции в аналитичекой форме.
| Пример | Функция | Прохождение через ось абсцисс | Прохождение через ось ординат |
|---|---|---|---|
| 1 | y = x^2 | x = 0 | y = 0 |
| 2 | y = sin(x) | x = 0, ±π, ±2π, ... | Не пересекает |
| 3 | y = 1/x | Не пересекает | x = 0, ±1, ±2, ... |
В таблице приведены примеры функций и их прохождение через оси. Аналитический подход позволяет с легкостью определить, пересекает ли функция оси абсцисс и ординат, и найти точки пересечения.
Графический метод для точного представления графика функции
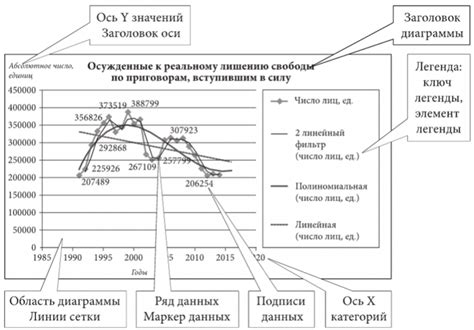
Для построения графика функции с помощью графического метода необходимо:
- Выбрать систему координат (обычно используются прямоугольные координаты);
- Задать интервалы изменения аргумента и функции;
- Найти значения функции для различных значений аргумента из выбранных интервалов;
- Соединить полученные точки графиком.
Графический метод позволяет легко определить такие характеристики функции, как экстремумы, нули функции, интервалы возрастания и убывания, асимптоты и другие особенности графика. Благодаря этому методу можно получить точное представление о поведении функции и легко отобразить его на графике.
Графический метод также может использоваться для анализа зависимостей между несколькими функциями. Путем построения графиков нескольких функций на одной системе координат можно установить их взаимное положение и визуально оценить их взаимосвязь.
Использование графического метода позволяет исследовать функции, определить их основные характеристики и получить наглядное представление о законах изменения функции. Этот метод является незаменимым инструментом для точного представления графика функции и позволяет улучшить понимание ее поведения.
Компьютерное моделирование для определения прохождения графика функции
Компьютерное моделирование позволяет визуализировать график функции и анализировать его прохождение через различные точки и интервалы. Программные средства для моделирования обычно предоставляют возможность задать формулу функции и диапазон значений для аргумента.
С помощью компьютерного моделирования можно быстро и точно определить точки пересечения графика функции с осями координат, экстремумы, интервалы возрастания и убывания, а также асимптоты. Моделирование позволяет получить графическое представление зависимости функции от ее аргумента и визуально наглядно показать особенности прохождения этой зависимости.
Таким образом, компьютерное моделирование становится незаменимым инструментом для определения прохождения графика функции, позволяя получить точное представление этой информации и провести детальный анализ поведения функции.
Экспериментальные исследования прохождения графика функции для его точного представления

Для достижения точного представления графика функции необходимо провести экспериментальные исследования прохождения этого графика. Эти исследования позволяют выявить особенности поведения функции и определить точное представление графика.
Одним из методов экспериментальных исследований является построение графика функции на координатной плоскости. Для этого необходимо знать значения функции в различных точках и соединить эти точки отрезками прямых. Таким образом, можно получить аппроксимацию графика, а затем провести интерполяцию для получения точного представления.
Еще одним методом исследования является использование математических моделей. С помощью таких моделей можно представить функцию в виде аналитического выражения и аппроксимировать график на основе этих уравнений. Затем проводится анализ полученной аппроксимации и корректировка модели для достижения более точного представления графика.
Для более точного определения прохождения графика функции часто применяются методы численного анализа. С их помощью можно вычислить значения функции в различных точках и провести аппроксимацию графика. Они позволяют учесть даже небольшие отклонения и получить более точное представление графика.
Экспериментальные исследования прохождения графика функции являются важным этапом для достижения его точного представления. Они позволяют выявить особенности поведения функции, провести анализ и корректировку моделей, а также учесть небольшие отклонения. Это позволяет получить наиболее точное и надежное представление графика функции.