Токовые линии треугольника являются важным инструментом в области геометрии и математики. Они представляют собой геометрические кривые, получаемые путем соединения точек на треугольнике, в которых пара сторон пересекается. Токовые линии предоставляют информацию о направлении тока и его распределении внутри треугольника.
Для определения токовых линий треугольника можно использовать различные методы. Одним из таких методов является метод векторного анализа. Суть метода заключается в вычислении градиента векторного поля, представляющего собой ток в каждой точке треугольника. Полученные градиенты указывают направление и силу токовых линий. Этот метод позволяет точно определить форму и распределение токовых линий треугольника.
Применение токовых линий треугольника находит свое применение в различных областях, таких как физика, электротехника, аэродинамика и гидродинамика. Например, в физике токовые линии треугольника используются для моделирования электромагнитных полей и исследования их свойств. В электротехнике они могут помочь в определении электрического потенциала и распределения заряда в системе. В аэродинамике и гидродинамике токовые линии применяются для анализа потоков жидкости и газа вокруг объектов и определения силы сопротивления.
Геометрический подход

Основной идеей геометрического подхода является использование геометрических принципов для расчета и отображения токовых линий треугольника. Для этого строятся специальные геометрические фигуры, в которых отображается направление и сила токовых линий.
Одна из ключевых геометрических фигур, используемых в геометрическом подходе, - это треугольник. Треугольник позволяет отобразить все три стороны токовых линий и их взаимное влияние на друг друга.
Для построения треугольника используются специальные правила и законы, которые позволяют точно определить его форму и размеры. Например, для определения стороны треугольника можно использовать закон синусов или закон косинусов.
Важным элементом геометрического подхода является также использование таблиц и графиков для визуализации результатов анализа токовых линий. Таблицы могут содержать значения токов, силы и направления токовых линий для каждой стороны треугольника. Графики позволяют наглядно представить изменение токовых линий в зависимости от входных параметров или времени.
| Ток | Сила | Направление |
|---|---|---|
| Ток 1 | Сила 1 | Направление 1 |
| Ток 2 | Сила 2 | Направление 2 |
| Ток 3 | Сила 3 | Направление 3 |
Геометрический подход широко используется в различных областях, связанных с анализом и определением токовых линий треугольника, таких как электротехника, физика и математика. Он позволяет получить достоверные и точные результаты и является надежным инструментом в решении различных практических задач.
Использование векторных операций

Векторные операции широко используются при анализе и применении токовых линий треугольника. Векторное сложение и вычитание позволяют определить направление и силу токов в различных участках треугольника.
Для определения тока в каждой из сторон треугольника можно использовать формулу:
I = V / R
где I - ток, V - напряжение, R - сопротивление.
Применение векторных операций также позволяет определить результат суперпозиции токов в треугольнике. Суперпозиция токов возникает при прохождении тока через различные участки треугольника.
Для решения задач по определению токовых линий треугольника с использованием векторных операций необходимо знать величину и направление тока в каждой из сторон треугольника. Затем можно применять законы Кирхгофа и другие методы, чтобы определить искомые значения.
Векторные операции являются мощным инструментом при работе с токовыми линиями треугольника, позволяя определить направление и силу токов, а также решить задачи по суперпозиции.
Матричные методы и линейная алгебра

Один из ключевых моментов при применении матричных методов - это представление схемы треугольника в виде системы уравнений, где каждому элементу схемы соответствует уравнение. Эти уравнения могут быть записаны в матричной форме, где матрица представляет собой коэффициенты перед неизвестными, а столбец - значения суммарных токов.
С помощью линейной алгебры и матричных операций можно решить системы уравнений и определить значения токов на каждой ветви треугольника. Также можно вычислить суммарные токи, определить зависимости между элементами схемы и оценить их влияние на результаты измерений.
Другим важным моментом является использование матричных методов для анализа токовых линий. Путем преобразования исходных данных и вычислений можно получить информацию о распределении токов внутри треугольника, о наличии и направлении токовых линий и о связи между элементами схемы.
Таким образом, матричные методы и линейная алгебра являются эффективными инструментами для анализа и решения задач, связанных с токовыми линиями треугольника. Использование этих методов позволяет получить более точные и объективные результаты, а также сократить время и усилия при проведении измерений и исследований.
Аналитическое решение системы уравнений
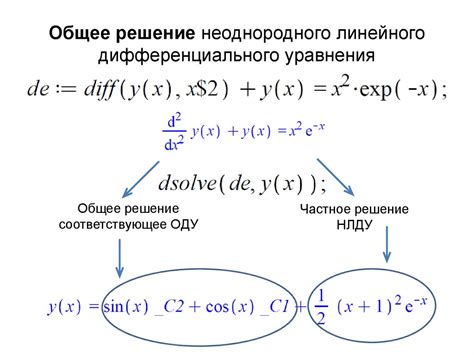
Для определения токовых линий треугольника возможно использование аналитического решения системы уравнений. Этот метод позволяет точно определить поведение токов в треугольнике и получить точные значения для каждой линии.
Аналитическое решение системы уравнений основывается на применении метода Кирхгофа для анализа схем электрических цепей. Для треугольника состоящего из трех резисторов, мы можем записать систему уравнений, которая описывает сумму напряжений в каждом резисторе равной нулю.
Решение этой системы уравнений позволяет определить значения токов в каждом резисторе, а следовательно и форму токовых линий внутри треугольника.
Аналитическое решение системы уравнений может быть использовано для определения оптимального распределения токов при проектировании электрических цепей. Также это решение может помочь в анализе различных электрических систем и схем в научных исследованиях.
Использование аналитического решения системы уравнений требует знания основных законов электричества и умения работать с алгебраическими уравнениями. Этот метод может быть сложным для начинающих, однако он предоставляет точные результаты, которые могут быть проверены и использованы в различных практических ситуациях.
Учет эффектов магнитного поля
При анализе токовых линий треугольника необходимо учитывать эффекты магнитного поля, которые оказывают влияние на формирование этих линий. Магнитное поле создается движущимися зарядами и намагниченными материалами.
При проникновении электрического тока через проводник, создается магнитное поле, которое окружает проводник. Форма и направление линий магнитного поля зависит от конфигурации проводников и величины тока.
Влияние магнитного поля на токовые линии треугольника проявляется в изменении их формы и направления. Магнитное поле может сжимать или расширять линии тока, а также изменять их направление.
Для учета эффектов магнитного поля при анализе токовых линий треугольника необходимо применять специальные техники и методы. Одним из таких методов является использование закона Био-Савара, который позволяет определить магнитное поле, создаваемое током. Этот закон основывается на принципе взаимодействия движущегося тока с магнитным полем.
Использование компьютерных программ и расчетных моделей
Для определения и применения токовых линий треугольника можно использовать различные компьютерные программы и расчетные модели. Они позволяют провести точный и надежный анализ электромагнитного поля в треугольнике, определить направление токов и оценить распределение энергии.
Одной из самых популярных программ для моделирования электрических полей является ANSYS Maxwell. С ее помощью можно создать расчетную модель треугольника и провести анализ электромагнитного поля. Программа предоставляет широкие возможности для визуализации результата, а также позволяет рассчитать различные параметры, такие как силы взаимодействия между токами и напряжение на границах треугольника.
Еще одной популярной программой является CST Studio Suite. Она обладает мощными инструментами для решения задач электромагнетизма и позволяет провести детальный анализ токовых линий треугольника. С ее помощью можно определить распределение энергии внутри треугольника и найти оптимальное решение для различных задач.
Nastran – еще одна расчетная программа, широко используемая в инженерии. Она позволяет решить большой класс задач, включая анализ токовых линий треугольника. Программа предлагает различные методы и алгоритмы для нахождения решения и позволяет получить точные результаты в кратчайшие сроки.
Использование компьютерных программ и расчетных моделей позволяет существенно упростить и ускорить процесс определения и применения токовых линий треугольника. Они предоставляют возможность провести точный анализ электромагнитного поля и получить детальную информацию о распределении токов. Такой подход позволяет оценить возможные риски и принять эффективные меры по оптимизации работы системы.
Применение токовых линий треугольника в практических задачах

Одним из практических применений токовых линий треугольника является расчет магнитного поля вокруг проводников при различных комбинациях токов. Например, при известных значениях токов и расстояний между проводниками можно определить силу взаимодействия или электромагнитный момент системы.
Другим применением является анализ электромагнитных взаимодействий в электрических машинах. Управление и оптимизация работы электродвигателей, генераторов и трансформаторов требует понимания распределения магнитного поля внутри и вокруг этих устройств. Токовые линии треугольника позволяют наглядно представить эти процессы и определить оптимальные параметры конструкции для повышения эффективности и надежности работы.
Еще одно применение токовых линий треугольника – создание электромагнитных замков и систем безопасности, которые основаны на взаимодействии магнитных полей. Путем правильной конфигурации проводников и токов можно создать универсальное электромагнитное поле, которое будет воздействовать на объекты, имеющие определенные свойства. Это может быть использовано для защиты от несанкционированного доступа, обнаружения металлических предметов или мониторинга движения объектов в пространстве.