Графы являются важным инструментом в анализе и моделировании различных систем. Один из наиболее фундаментальных параметров графа - это количество ребер. Количество ребер влияет на связность графа и позволяет оценить сложность системы, представленной графом. В этой статье мы рассмотрим несколько методов определения количества ребер графа и обсудим их особенности.

Первый метод основывается на определении количества ребер по формуле Эйлера. Формула Эйлера устанавливает связь между количеством вершин, ребер и граней в плоском графе. Формула имеет вид V - E + F = 2, где V - количество вершин, E - количество ребер, а F - количество граней. Используя эту формулу, мы можем выразить количество ребер E как E = V + 2 - F. Однако данный метод применим только для плоских графов, а для не плоских графов другие методы необходимы.

Второй метод основывается на матрице смежности графа. Матрица смежности - это таблица, где каждая ячейка указывает наличие или отсутствие ребра между двумя вершинами. Сумма элементов матрицы смежности дает общее количество уникальных ребер в графе. Однако данный метод не учитывает кратные ребра и работает только для неориентированных графов. Для ориентированных графов необходимо использовать матрицу инцидентности.

Третий метод основывается на обходе графа с помощью алгоритмов поиска в глубину или поиска в ширину. При обходе графа алгоритмом поиска в глубину или в ширину мы можем подсчитать количество пройденных ребер. Однако данный метод требует более сложных вычислений и имеет ограниченную применимость в случае больших графов.

Методы счета ребер

Метод подсчета по формуле

Самым простым методом определения количества ребер в графе является использование формулы Эйлера. Формула Эйлера устанавливает связь между количеством вершин, ребер и граней в связном плоском графе. В случае, если граф не является плоским или несвязным, формула Эйлера может не применяться.

Формула Эйлера выглядит следующим образом:

V - E + F = 2

Где V - количество вершин, E - количество ребер, а F - количество граней в графе.

Метод подсчета по матрице смежности

Другим методом определения количества ребер является использование матрицы смежности графа. Матрица смежности представляет граф в виде двумерного массива. Для неориентированного графа количество ребер равно половине суммы элементов на главной диагонали матрицы смежности.

Метод подсчета по списку смежности

Третий метод определения количества ребер в графе заключается в использовании списка смежности. В списке смежности каждой вершины указываются все смежные с ней вершины. Количество ребер равно половине суммы длин всех списков смежности.

Использование указанных методов позволяет точно определить количество ребер в графе независимо от его типа и структуры.

Методы базирующиеся на матрице смежности

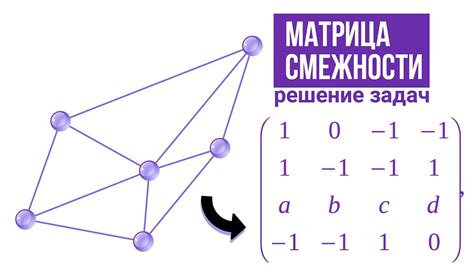
Один из основных методов определения количества ребер графа основывается на его матрице смежности. Матрица смежности представляет собой квадратную таблицу, где столбцы и строки соответствуют вершинам графа, а элементы таблицы указывают наличие или отсутствие ребра между соответствующими вершинами.

Для определения количества ребер графа по его матрице смежности, необходимо посчитать количество единиц в этой матрице, за исключением диагональных элементов. Так как каждое ребро в графе представляется единицей в матрице смежности, то сумма всех элементов матрицы дает общее количество ребер.

Преимуществом этого метода является его простота и понятность. Данный метод работает для любого типа графов, включая ориентированные и взвешенные графы.

Однако, этот метод имеет некоторые особенности, которые могут оказаться недостатком в некоторых случаях. Например, при работе с большими графами, матрица смежности может занимать большой объем памяти, что может стать проблемой при ограниченных ресурсах. Также, матрица смежности неэффективна для работы с графами, содержащими большое количество ребер, т.к. большая часть ее элементов будет равна нулю.

В целом, методы определения количества ребер графа, базирующиеся на матрице смежности, являются надежными и широко применяемыми. Они обеспечивают точный и понятный подсчет количества ребер в графе и могут быть использованы в большинстве случаев.

Методы на основе матрицы инцидентности

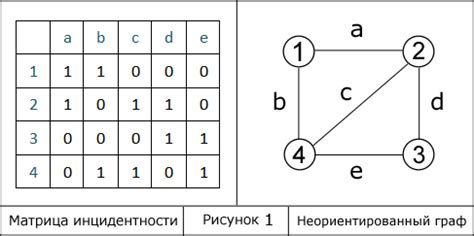
Первый метод заключается в подсчете количества столбцов в матрице инцидентности. Каждый столбец соответствует ребру, поэтому их количество равно количеству ребер в графе. Этот метод прост и удобен, но не учитывает возможные повторения ребер или петли.

Второй метод основан на подсчете суммы элементов в каждом столбце матрицы инцидентности. Если каждому ребру присвоить единичный вес (то есть элементам матрицы инцидентности присвоить значение 1), то сумма элементов в каждом столбце будет равна количеству инцидентных ему ребер. Следовательно, сумма всех элементов в матрице будет равна общему количеству ребер в графе.

Третий метод учитывает возможные повторения ребер и петли. Для этого необходимо просуммировать все ненулевые элементы матрицы инцидентности. Результат будет равен количеству ребер в графе, с учетом всех возможных повторений и петель.

Все эти методы применимы к графу любой природы: ориентированному, неориентированному, взвешенному и невзвешенному. Однако, перед использованием любого из этих методов, следует убедиться в правильности построения матрицы инцидентности, чтобы избежать ошибочных результатов.