Логарифмическая функция является одной из важнейших математических функций, которая находит применение в различных областях науки и техники. Для правильного использования этой функции необходимо определить область определения, то есть множество всех допустимых значений аргумента, при которых функция определена и имеет смысл.
Существует несколько методов определения области определения логарифмической функции. Первый метод основан на анализе аргумента функции. Логарифмическая функция определена только для положительных значений аргумента. Таким образом, область определения функции обычно представляет собой множество всех действительных положительных чисел.
Однако, в некоторых случаях, область определения может быть ограничена дополнительными условиями. Например, в логарифмической функции с основанием больше единицы, аргумент не должен быть равен нулю. Поэтому в данном случае область определения будет состоять из всех положительных чисел, кроме нуля.
Примером расчета области определения может служить задача нахождения значения логарифма от некоторого выражения. Допустим, требуется найти значение логарифма от выражения (x-3)/(x+2). При анализе аргумента данного выражения видно, что он может быть любым числом, кроме -2. Поэтому область определения функции будет состоять из всех значений аргумента, кроме -2.
Определение области определения

Для логарифмической функции с основанием a область определения определяется условием, при котором аргумент x входит в множество положительных чисел, записывается как x > 0.
Область определения логарифмической функции можно представить в виде отрезка на числовой оси, начиная с положительного числа 0 и изначально не имеющего верхней границы.
Значит, для логарифмической функции y = loga(x) где a > 0 и a ≠ 1, область определения будет множеством всех положительных значений x: x > 0.
Методы определения области определения логарифмической функции

Существуют несколько методов для определения области определения логарифмической функции:
- Анализ аргумента. Логарифмическая функция определена только для положительных аргументов. Поэтому сначала необходимо исключить нулевые и отрицательные значения аргумента, поскольку они противоречат определению логарифма.
- Ограничения на аргумент. Некоторые логарифмические функции имеют ограничения на допустимые значения аргумента. Например, для логарифма по основанию 10 аргумент должен быть действительным числом, то есть принадлежать множеству действительных чисел.
- Знак аргумента. Для логарифма по основанию 10 аргумент должен быть положительным, поэтому отрицательные значения аргумента также исключаются из области определения.
- Условия знака. Некоторым логарифмическим функциям необходимо дополнительно учесть определенные условия знака аргумента. Например, для натурального логарифма аргумент должен быть положительным и не равным 1.
Примером расчета области определения логарифмической функции может служить расчет области определения функции № = log(x), где х – аргумент функции.
Анализ аргумента показывает, что x должен быть положительным числом, так как логарифм отрицательного числа не определен.
Ограничение на аргумент определяет, что x должен принадлежать множеству действительных чисел.
Знак аргумента показывает, что x не может быть отрицательным числом, иначе функция также не будет определена. Поэтому область определения логарифмической функции выглядит как множество всех положительных действительных чисел.
Примеры расчетов области определения для простых логарифмических функций

- Функция y = log(x)
- Функция y = log2(x)
- Функция y = ln(x)
- Функция y = log(a, x)
Для данной функции, область определения задается условием x > 0, так как логарифм отрицательного числа не определен.
Область определения для логарифма по основанию 2 определяется условием x > 0. При этом, аргумент должен быть положительным числом.
Для натурального логарифма, область определения задается условием x > 0, так как логарифм отрицательного числа не имеет смысла.
Для логарифма по произвольному основанию a, область определения задается условием x > 0. При этом, аргумент должен быть положительным числом.
При расчете области определения логарифмической функции необходимо учитывать ограничения на аргументы функции, чтобы избежать получения неопределенных значений или абсурдных результатов. Такие ограничения могут быть связаны со свойствами логарифмов и требованиями к аргументам функции.
Примеры сложных логарифмических функций и их области определения
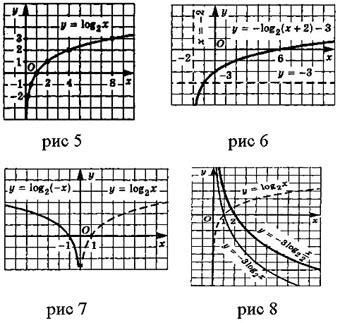
Рассмотрим несколько примеров сложных логарифмических функций и их областей определения:
| Функция | Область определения |
|---|---|
| $$f(x) = \log_2(x^2 - 4x + 3)$$ | $$x^2 - 4x + 3 > 0$$ $$x \in (-\infty, 1) \cup (3, \infty)$$ |
| $$f(x) = \ln(\sqrt{x} - 1)$$ | $$x \geq 1$$ |
| $$f(x) = \log_{10}(1 - \frac{1}{x})$$ | $$x > 1$$ |
Первая функция имеет логарифм от полинома в основании. Область определения определяется условием, при котором значение подлежит логарифмированию. В данном случае, полином должен быть больше нуля.
Вторая и третья функции имеют разные основания логарифма. Область определения в этих случаях ограничена допустимыми значениями выражения внутри логарифма.
Знание области определения логарифмических функций позволяет избежать ошибок при их использовании и проведении вычислений. Важно помнить, что логарифмические функции могут иметь различные области определения в зависимости от вида и основания функции.
Расчеты граничных значений области определения для логарифмических функций

Область определения логарифмической функции определяется значениями, при которых функция принимает реальные значения. Для вычисления этих граничных значений необходимо учесть следующие особенности:
- Логарифм с отрицательным основанием не имеет определения, так как результатом будет комплексное число. Поэтому основание логарифма всегда должно быть положительным.
- Логарифм с нулевым основанием не имеет определения, так как не существует степени, при которой получится нуль. Поэтому основание логарифма также не должно равняться нулю.
- Логарифм с нулем аргумента не имеет определения, так как не существует числа, возводя которое в некоторую степень, можно получить нуль. Поэтому аргумент логарифма всегда должен быть положительным числом.
Таким образом, область определения для обычного логарифма (с основанием 10) выглядит следующим образом:
Допустимыми значениями для аргумента являются все положительные числа, за исключением нуля.
Если мы имеем дело с логарифмической функцией с другим основанием, например, основанием a, то область определения будет выглядеть следующим образом:
Допустимыми значениями для аргумента являются все положительные числа, за исключением нуля.
Следует помнить, что при работе с логарифмическими функциями необходимо проверять область определения каждой функции в отдельности, так как они могут отличаться основанием и предназначением.