Определение принадлежности точки окружности является одной из важнейших задач в геометрии. Существует несколько методов, позволяющих решить эту задачу. В данной статье мы рассмотрим несколько примеров и подробно объясним каждый из них.
Первый метод основан на уравнении окружности. Если имеется уравнение окружности в канонической форме (x - a)² + (y - b)² = r², где (a, b) - координаты центра окружности, r - радиус окружности, то для определения принадлежности точки (x₀, y₀) необходимо подставить её координаты в это уравнение. Если полученное уравнение исходное уравнение окружности равны, то точка принадлежит окружности. Если нет, то точка лежит вне окружности.
Второй метод основан на используемой формуле длины окружности. Если известна длина окружности L и радиус r, то можно вычислить угол α, опирающийся на дугу, длина которой равна L/2π. Затем можно проверить, лежит ли точка на этой дуге. Для этого нужно вычислить угол β, между радиусом, проведенным к точке, и положительным направлением оси OX. Если β = α, то точка принадлежит окружности, если нет, то точка лежит вне окружности.
Третий метод основан на использовании векторов. Если имеются векторы \vec{OA} и \vec{OB}, где O - центр окружности, A - точка окружности, B - произвольная точка, тогда можно построить векторное произведение \vec{OA} \times \vec{OB}. Если результат векторного произведения равен нулю, то точка лежит на окружности. Если результат отличен от нуля, то точка лежит вне окружности.
Методы нахождения точки на окружности: что это такое?

Методы нахождения точки на окружности используются для определения принадлежности точки к окружности. Задача заключается в том, чтобы определить, лежит ли точка на окружности или находится внутри/снаружи нее.
Существует несколько методов для решения этой задачи, самые популярные из которых включают:
- Метод уравнения окружности: данный метод основан на использовании сравнения расстояния от данной точки до центра окружности и радиуса. Если расстояние равно радиусу, то точка лежит на окружности. Если расстояние больше радиуса, то точка находится вне окружности. Если расстояние меньше радиуса, то точка находится внутри окружности.
- Метод координат точки: в данном методе используются координаты точки и центра окружности. Расстояние между точкой и центром окружности вычисляется с использованием формулы расстояния между двумя точками. Если расстояние равно радиусу, то точка лежит на окружности. Если расстояние больше радиуса, то точка находится вне окружности. Если расстояние меньше радиуса, то точка находится внутри окружности.
- Метод углов: данный метод основан на использовании геометрических свойств окружности. Угол между радиусом, проведенным из центра окружности к данной точке, и любым другим радиусом на окружности можно вычислить с использованием тригонометрии. Если угол равен 90 градусам, то точка лежит на окружности. Если угол больше 90 градусов, то точка находится вне окружности. Если угол меньше 90 градусов, то точка находится внутри окружности.
Выбор метода зависит от конкретной задачи и доступных данных. Каждый из этих методов имеет свои преимущества и ограничения, поэтому важно выбрать наиболее подходящий метод в каждой конкретной ситуации.
Геометрический метод: как определить принадлежность точки окружности?

Для применения геометрического метода необходимо знать центр окружности и её радиус. Окружность можно представить в виде уравнения (x - a)² + (y - b)² = r², где (a, b) - координаты центра окружности, r - радиус.
Чтобы определить принадлежность точки с координатами (x, y) окружности, можно проверить условие данного уравнения:
- Если (x - a)² + (y - b)² , то точка находится внутри окружности.
- Если (x - a)² + (y - b)² = r², то точка лежит на окружности.
- Если (x - a)² + (y - b)² > r², то точка находится вне окружности.
Таким образом, геометрический метод позволяет определить принадлежность точки окружности на основе её координат и уравнения окружности. Этот метод является точным и достаточно простым для понимания и применения.
Аналитический метод: как найти принадлежность точки к окружности с помощью формул?

Аналитический метод определения принадлежности точки к окружности основан на использовании алгебраических формул и критериях равенства выражений. С его помощью можно легко и точно определить, лежит ли данная точка внутри окружности, на ее границе или вне ее.
Для этого необходимо знать координаты центра окружности (Cx, Cy) и радиус окружности R. Также известны координаты точки (Px, Py), принадлежность которой нужно определить.
С помощью аналитического метода можно воспользоваться одной из следующих формул:
| Формула | Описание |
|---|---|
| (Px - Cx)^2 + (Py - Cy)^2 | Точка (Px, Py) лежит внутри окружности |
| (Px - Cx)^2 + (Py - Cy)^2 = R^2 | Точка (Px, Py) лежит на границе окружности |
| (Px - Cx)^2 + (Py - Cy)^2 > R^2 | Точка (Px, Py) лежит вне окружности |
Если значение левой части формулы меньше, равно или больше значения правой части, то соответственно точка лежит внутри окружности, на ее границе или вне ее.
Аналитический метод позволяет с легкостью и точностью определить принадлежность точки к окружности без необходимости дополнительных геометрических построений. Это особенно полезно при работе с большим количеством точек и сложных окружностях.
Положение точки внутри окружности: примеры и объяснение

По определению, точка принадлежит окружности, если расстояние от этой точки до центра окружности равно радиусу.
Для определения положения точки внутри окружности можно использовать следующий алгоритм:
- Найдите расстояние от данной точки до центра окружности с помощью формулы расстояния между двумя точками.
- Сравните полученное расстояние с радиусом окружности.
- Если расстояние равно радиусу, то точка лежит на окружности.
- Если расстояние меньше радиуса, то точка находится внутри окружности.
- Если расстояние больше радиуса, то точка находится вне окружности.
Пример 1:
Дана окружность с центром в точке (0, 0) и радиусом 5. Для точки А(-3, 4) проверим ее положение относительно окружности.
Расстояние от точки А до центра окружности:
Расстояние = √((-3 - 0)² + (4 - 0)²) = √((-3)² + 4²) = √(9 + 16) = √(25) = 5.
Расстояние равно радиусу окружности (5), значит точка А лежит на окружности.
Пример 2:
Рассмотрим теперь точку B(2, 2) и окружность с центром в точке (0, 0) и радиусом 5. Проверим, где находится точка B относительно окружности.
Расстояние от точки B до центра окружности:
Расстояние = √((2 - 0)² + (2 - 0)²) = √(2² + 2²) = √(4 + 4) = √(8) ≈ 2.83.
Расстояние меньше радиуса окружности (5), значит точка B находится внутри окружности.
Пример 3:
Пусть теперь есть точка C(10, -3) и окружность с центром в точке (0, 0) и радиусом 5. Проверим, где находится точка C относительно окружности.
Расстояние от точки C до центра окружности:
Расстояние = √((10 - 0)² + (-3 - 0)²) = √(10² + (-3)²) = √(100 + 9) = √(109) ≈ 10.44.
Расстояние больше радиуса окружности (5), значит точка C находится вне окружности.
Таким образом, определить положение точки внутри окружности можно, сравнив расстояние от точки до центра окружности с радиусом. При равности расстояния и радиуса, точка лежит на окружности, при меньшем расстоянии – точка находится внутри окружности, и при большем расстоянии – точка находится вне окружности.
Положение точки вне окружности: примеры и объяснение
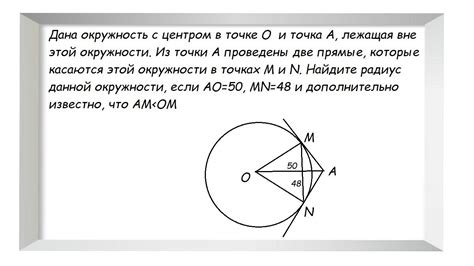
Как определить, находится ли точка вне окружности? Существует несколько методов. Один из них - использование координат точек и уравнения окружности.
Предположим, что у нас есть окружность с центром в точке (a, b) и радиусом r. Нужно проверить, находится ли точка с координатами (x, y) вне этой окружности.
Для начала, вычислим расстояние между центром окружности и точкой. Используя теорему Пифагора, расстояние (d) можно найти по формуле:
d = √((x - a)² + (y - b)²)
Затем, сравним это расстояние с радиусом окружности (r). Если расстояние больше радиуса, то точка находится вне окружности. Если расстояние меньше или равно радиусу, то точка находится внутри окружности.
Ниже приведен пример, показывающий, как использовать эту формулу для определения положения точки вне окружности:
// Определим координаты центра окружности и радиус
let a = 2;
let b = 3;
let r = 5;
// Определим координаты точки
let x = 7;
let y = 4;
// Вычислим расстояние между точкой и центром окружности
let distance = Math.sqrt((x - a)**2 + (y - b)**2);
// Сравним расстояние с радиусом окружности
if (distance > r) {
console.log("Точка находится вне окружности");
} else {
console.log("Точка находится внутри окружности");
}
В этом примере, точка с координатами (7, 4) находится вне окружности с центром в точке (2, 3) и радиусом 5.
Таким образом, использование координат и уравнения окружности позволяет определить положение точки вне окружности. Этот метод основывается на вычислении расстояния между точкой и центром окружности, и сравнении этого расстояния с радиусом окружности.
Положение точки на окружности: примеры и объяснение
1. Метод с использованием радиус-вектора:
Рассмотрим точку A с координатами (x, y) и радиус-вектором r. Возьмем точку O, которая является центром окружности. Если длина радиус-вектора r совпадает с радиусом окружности R, то точка A лежит на окружности. В противном случае, точка A будет находиться внутри или вне окружности.
2. Метод с использованием уравнения окружности:
Уравнение окружности имеет вид (x - a)^2 + (y - b)^2 = R^2, где (a, b) - координаты центра окружности, R - радиус окружности. Подставим координаты точки A в это уравнение. Если уравнение выполняется, то точка A лежит на окружности. Если уравнение не выполняется, точка A будет находиться внутри или вне окружности.
3. Метод с использованием угла:
Для определения положения точки A на окружности построим отрезок OA (где O - центр окружности) и найдем его угол α с положительным направлением вдоль окружности. Затем построим угол β между отрезком OA и отрезком AB, где B - произвольная точка на окружности. Если угол α равен углу β, то точка A лежит на окружности. Если углы не равны, точка A будет находиться внутри или вне окружности.
Таким образом, существуют различные методы определения положения точки на окружности. Каждый из этих методов имеет свои преимущества и может применяться в разных ситуациях. Знание этих методов поможет вам решать задачи, связанные с окружностями и их свойствами.
Практическое применение методов: примеры использования на практике

- Геодезия: методы определения принадлежности точки окружности используются для определения координат и расстояний между объектами на земной поверхности. Например, геодезисты могут использовать эти методы для определения принадлежности точки геодезической сетке или границе участка земли.
- Компьютерная графика: методы определения принадлежности точки окружности используются для создания и манипуляции графическими объектами на экране. Например, при построении компьютерной игры разработчики могут использовать эти методы для определения столкновений между персонажами и объектами окружающей среды.
- Физика: методы определения принадлежности точки окружности являются неотъемлемой частью многих физических моделей и экспериментов. Например, при моделировании движения тела в пространстве физики используют эти методы для определения принадлежности точки траектории движения.
Все эти примеры демонстрируют практическую значимость методов определения принадлежности точки окружности. Понимание этих методов и их корректное применение позволяют решать сложные задачи в различных областях науки и техники.
Возможные ошибки при определении принадлежности точки окружности

Одной из возможных ошибок является использование неправильных формул для определения принадлежности точки окружности. Если формула неправильно выбрана или неправильно применена, результат может быть искажен. Поэтому важно внимательно изучить методы и убедиться, что используется правильная формула.
Другой возможной ошибкой является неверное использование координат точки и центра окружности при расчетах. Если координаты указаны неправильно или их переставили местами, результат также будет неверным. Поэтому важно внимательно проверять введенные данные и их правильность перед началом расчетов.
Также, при работе с окружностями может возникнуть ошибка из-за округления чисел. Когда происходят сложные математические операции, возможны незначительные погрешности, которые могут повлиять на результат определения принадлежности точки окружности. В таких случаях, рекомендуется учитывать погрешности и округлять результаты до определенного числа знаков после запятой для получения более точных результатов.
Также следует учитывать, что некоторые методы, основанные на аналитической геометрии, могут быть применимы только для определенных типов окружностей или точек. Например, некоторые методы могут работать только с окружностями, заданными уравнением в канонической форме, а не с окружностями, заданными в параметрической форме. Поэтому при применении методов следует учитывать их ограничения и проверять их применимость к конкретной задаче.
| Возможная ошибка | Последствия |
|---|---|
| Неправильная формула | Неверный результат |
| Неправильные координаты | Неверный результат |
| Ошибка округления чисел | Неверный результат |
| Неприменимость метода | Неверный результат |
Важно учитывать данные возможные ошибки и принимать меры для их предотвращения или исправления. Проведение дополнительных проверок и тестов может помочь убедиться в правильности работы методов и получить точные результаты определения принадлежности точки окружности.