Пересечение графиков квадратичных функций - это одна из важных задач в алгебре и геометрии. Нахождение точек пересечения графиков позволяет решить множество прикладных задач в физике, экономике, инженерии и других областях. Существуют различные методы для решения этой задачи, включая аналитические и графические подходы.
Аналитические методы основаны на использовании алгебры и математического аппарата. Для нахождения точек пересечения графиков квадратичных функций необходимо решить систему уравнений, полученную путем приравнивания двух функций друг к другу. В этом случае необходимо приравнять квадратичные функции между собой и решить полученное уравнение. Полученные значения x будут являться абсциссами точек пересечения графиков.
Графические методы основаны на построении графиков функций и нахождении их точек пересечения графическим путем. Для этого необходимо построить графики квадратичных функций на одних осях и найти точки, в которых графики пересекаются. Эти точки будут являться точками пересечения графиков квадратичных функций.
Аналитические методы поиска точек пересечения графиков
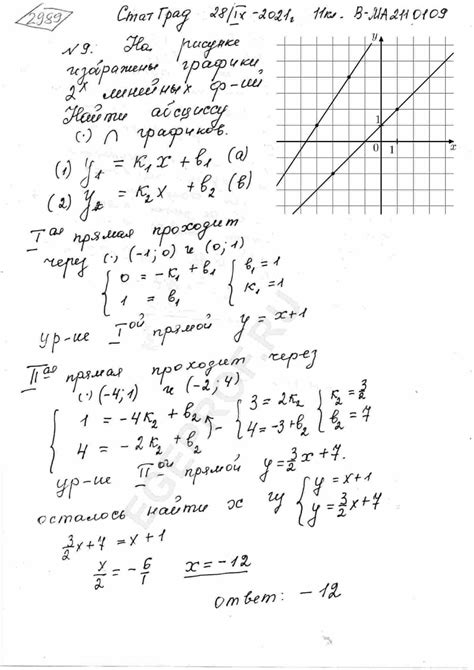
- Метод подстановки. В этом методе мы подставляем координаты точки пересечения в уравнение квадратичной функции и решаем полученное уравнение.
- Метод равенства функций. Суть метода заключается в приравнивании двух квадратичных функций и решении полученного уравнения.
- Метод графического построения. При помощи этого метода мы строим графики квадратичных функций на одной системе координат и находим точку пересечения графиков графически.
- Метод дискриминанта. Этот метод основан на дискриминанте квадратного трехчлена и позволяет найти координаты точки пересечения графиков.
Каждый из этих аналитических методов имеет свои преимущества и может быть использован в различных ситуациях. Используя эти методы, мы можем точно определить координаты точек пересечения графиков квадратичных функций, что облегчает решение многих практических задач.
Использование системы уравнений

Пусть имеются две квадратные функции f(x) = ax² + bx + c и g(x) = dx² + ex + f, где a, b, c, d, e, f - произвольные коэффициенты.
Чтобы найти точки пересечения графиков f(x) и g(x), необходимо решить систему уравнений f(x) = g(x), то есть ax² + bx + c = dx² + ex + f.
Для этого нужно привести уравнение к хорошо известной форме ax² + bx + c - dx² - ex - f = 0 и привести подобные члены. Затем полученное уравнение можно решить с помощью методов алгебры.
Решение системы уравнений позволяет определить значения x, при которых графики f(x) и g(x) пересекаются. Зная значения x, можно определить и соответствующие им значения y, подставив их в любую из двух функций.
Использование системы уравнений является универсальным методом для поиска точек пересечения графиков квадратичных функций. Однако он требует некоторых навыков в решении систем уравнений и может быть более трудоемким по сравнению с другими методами.
В результате применения данного метода можно получить точные значения точек пересечения графиков, что позволяет более точно определить их координаты и взаимное положение на плоскости.
Метод дискриминанта
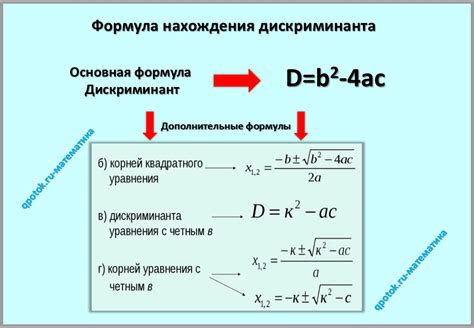
Для использования метода дискриминанта необходимо сначала представить квадратичное уравнение в общем виде:
ax^2 + bx + c = 0
где a, b и c - коэффициенты квадратичной функции.
Далее, используя формулу дискриминанта:
D = b^2 - 4ac
можно определить тип поведения графика квадратичной функции:
- Если D > 0, то график квадратичной функции пересекает ось X в двух точках;
- Если D = 0, то график квадратичной функции касается оси X в одной точке;
- Если D
Если D > 0, можно найти точки пересечения графика квадратичной функции с осью X, используя формулы:
- x1 = (-b + √D) / (2a)
- x2 = (-b - √D) / (2a)
где x1 и x2 - координаты точек пересечения графика с осью X.
Метод дискриминанта позволяет быстро определить, сколько и какие точки пересечения имеет график квадратичной функции с осью X. Он широко используется в математике и естественных науках для решения задач, связанных с аналитическими исследованиями графиков функций.
Применение формулы Виета
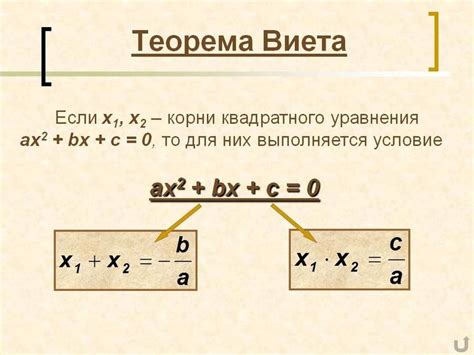
Формула Виета основана на том, что сумма корней квадратного уравнения равна отрицательному коэффициенту при старшей степени x, а произведение корней равно свободному члену.
Для квадратного уравнения вида ax^2 + bx + c = 0 формулы Виета имеют следующий вид:
| Сумма корней | Произведение корней |
|---|---|
| x1 + x2 = -b/a | x1 * x2 = c/a |
Если нам известны коэффициенты a, b и c уравнения, то можно найти сумму корней и их произведение с помощью этих формул.
Зная сумму и произведение корней, мы можем найти сами корни и использовать их для определения точек пересечения графиков двух квадратичных функций.
Графические методы поиска точек пересечения графиков
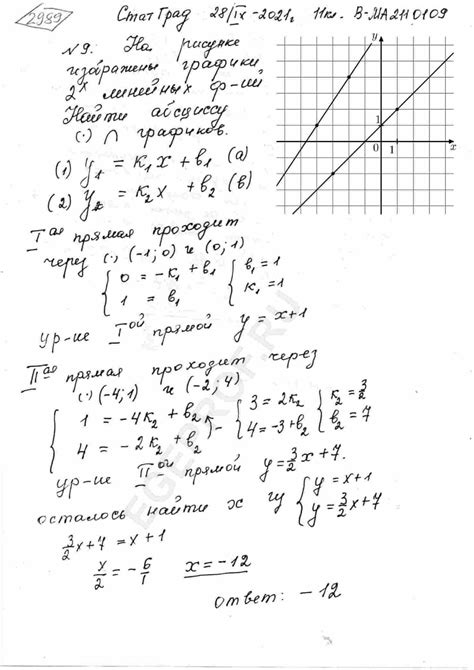
Графические методы поиска точек пересечения графиков квадратичных функций состоят в визуальном анализе графиков функций и определении мест их пересечения. Эти методы позволяют наглядно представить взаимное расположение графиков и найти точки пересечения без использования сложных математических вычислений.
Один из графических методов поиска точек пересечения графиков - метод построения графиков функций на координатной плоскости и наглядного определения мест их пересечения. Для этого необходимо построить графики функций и осмотреть получившийся график. Пересечение графиков отражает точки, в которых функции равны друг другу. Таким образом, точки пересечения графиков являются решениями уравнения, определяющего систему квадратных функций.
Еще один графический метод поиска точек пересечения графиков - метод использования графических калькуляторов или компьютерных программ. С помощью этих инструментов можно визуализировать графики двух функций на одном графике и автоматически определить их точки пересечения. Этот метод является особенно полезным при поиске точек пересечения сложных графиков или системы функций.
Таким образом, графические методы поиска точек пересечения графиков позволяют с легкостью определить точки пересечения квадратичных функций без использования сложных математических вычислений. Они предоставляют возможность наглядно представить взаимное расположение графиков и найти точки пересечения, что упрощает анализ и решение систем квадратных функций.
Построение графиков
Существуют различные способы построения графиков, однако наиболее распространенным и простым способом является использование координатной плоскости. Для построения графиков квадратичных функций часто используются следующие шаги:
- Определить диапазон значений аргумента, на котором будет строиться график. Например, определить интервал от -10 до 10.
- Вычислить значения функции для каждого значения аргумента в заданном диапазоне. Для этого подставить значения аргумента в уравнение функции.
- Построить точки на координатной плоскости, соответствующие найденным значениям функции. Соединить полученные точки линией.
- Добавить метки к осям координат и подписи к точкам графика.
График квадратичной функции может иметь различную форму: это может быть парабола, либо ветви параболы, направленные вниз или вверх. Форма графика зависит от коэффициента a в уравнении функции. Если a больше нуля, график будет иметь форму "улыбающейся" параболы, направленной вверх. Если a меньше нуля, график будет иметь форму "грустящей" параболы, направленной вниз.
Построение графиков квадратичных функций позволяет визуализировать и анализировать их основные характеристики, такие как вершина параболы, направление выпуклости, оси симметрии и точки пересечения с осями координат. Это помогает понять поведение функции и решать задачи, связанные с квадратичными уравнениями и неравенствами.