Косинус окружности – это понятие, которое может показаться необычным и неочевидным. Однако, на самом деле, это не что иное, как косинус угла с радиусом единица, который описывает точку на окружности. Достаточно интересное и полезное свойство, которое может пригодиться в различных технических задачах.
Для вычисления косинуса окружности необходимо знать ее радиус и угол, который она описывает. Угол измеряется в радианах и нередко обозначается греческой буквой θ (тета). Полный угол в окружности составляет 360° или 2π радиан. Отметим, что косинус угла равен отношению прилежащего катета к гипотенузе. В случае с окружностью катетом выступает радиус, а гипотенуза – длина окружности.
Для нахождения косинуса окружности можно использовать следующую формулу:
cos(θ) = x / r,
где θ – угол, x – прилежащий катет (в данном случае радиус), r – радиус окружности.
Таким образом, нахождение косинуса окружности сводится к делению радиуса на длину окружности, что позволяет определить, какую часть окружности описывает заданный угол.
Косинус окружности: определение и применение
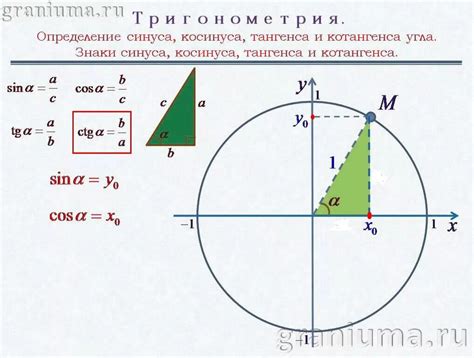
Косинус окружности широко используется в геометрии, физике и инженерии. Например, при решении задач связанных с движением по криволинейным трассам, определение косинуса окружности может помочь в расчетах радиуса поворота автомобиля или скорости на конкретном участке трассы. Кроме того, косинус окружности может использоваться в графическом моделировании для создания плавных кривых и анимации.
Косинус окружности вычисляется по формуле: cos(θ) = x / r, где θ - угол, x - координата точки по оси X, r - радиус окружности.
Знание косинуса окружности позволяет упростить решение задач, связанных с геометрией и движением по окружностям, а также находить решения для более сложных задач, используя тригонометрические свойства косинуса.
Изучение основ: что такое косинус окружности
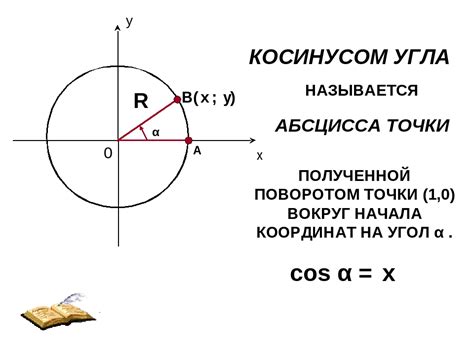
Косинус окружности обозначается с помощью функции cos(). Значение косинуса окружности всегда находится в диапазоне от -1 до 1. Косинус окружности имеет множество свойств и применений в науке и технике.
Например, косинус окружности может быть использован для определения угла между двумя векторами или для вычисления длины стороны треугольника, если известны две другие стороны и угол между ними. Он также широко применяется в физике, инженерии, компьютерной графике и других областях науки и техники.
Изучение косинуса окружности позволяет более глубоко понять геометрические и тригонометрические свойства окружности и применить их в различных задачах. Поэтому изучение этой математической функции является важным шагом в познании основ науки и техники.
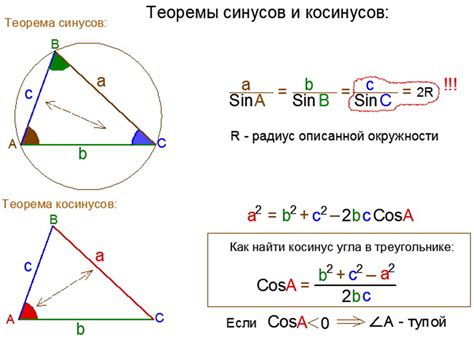
Применение косинуса окружности в геометрии и физике
В геометрии:
Косинус окружности – это функция, описывающая отношение длины прилежащего катета (стороны) треугольника к радиусу окружности. Геометрический смысл косинуса окружности заключается в определении угла между радиусом окружности и горизонтальной осью.
Косинус окружности широко используется в геометрии для вычисления различных параметров треугольников и кругов. Например, с его помощью можно рассчитать длину стороны треугольника по двум известным сторонам и углу между ними, а также найти площадь треугольника.
В физике:
Косинус окружности также находит применение в различных областях физики. Например, в механике он используется для анализа движения объектов по окружности, включая колебания и вращательное движение.
В электричестве и магнетизме косинус окружности помогает определять фазовые углы и характеристики периодических величин, а также для расчета векторных величин.
В оптике косинус окружности используется для определения уклона оптического кабеля, вычисления угла преломления и отражения света.
Таким образом, косинус окружности является важным математическим инструментом, широко применяемым в геометрии и физике для решения различных задач и расчетов.
Вычисление косинуса окружности: формулы и способы
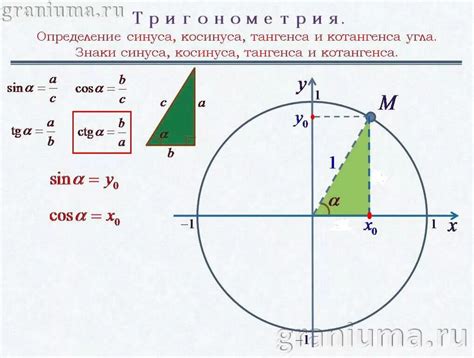
Вычисление косинуса окружности может быть полезно в различных областях, таких как физика, техника и геодезия. Существует несколько способов вычисления косинуса окружности, включая использование готовых формул и приближенных методов.
- Формула косинуса: Для нахождения косинуса угла в окружности можно использовать готовую формулу. Косинус угла можно вычислить по следующей формуле: cos(φ)=xc, где φ - угол, а xc - координата x точки на окружности.
- Приближенный метод: Если необходимо быстро и приближенно вычислить косинус окружности, можно воспользоваться рядом Маклорена или другими приближенными методами. Эти методы позволяют получить результат с заданной точностью при помощи ряда вычислений и приближений.
- Графический метод: Для визуализации и вычисления косинуса окружности можно использовать графический метод. Для этого строится график функции косинуса, который позволяет наглядно представить значения косинуса для различных углов.
Выбор метода вычисления косинуса окружности зависит от поставленной задачи и требуемой точности результата. Если нужен точный результат, то следует использовать формулу для вычисления косинуса окружности. Если важна скорость или приближенное значение, то можно воспользоваться приближенными методами или графическим методом.
Вычисление косинуса окружности является важной задачей в математике и других областях науки. Понимание формул и способов вычисления косинуса окружности позволяет решать сложные задачи и проводить точные измерения.