Смежные углы - это пары углов, которые имеют общую сторону и вершину. Они являются одной из основных концепций геометрии и широко используются в математических расчетах и решении задач. Но возникает вопрос: могут ли смежные углы быть тупыми?
Ответ на этот вопрос простой - да, смежные углы могут быть тупыми. Тупой угол - это угол, который больше 90 градусов, но меньше 180 градусов. Если с двух сторон общей вершины находятся тупые углы, то они будут смежными тупыми углами. Величина смежных углов может быть различной, но главное условие - они должны быть образованы общей стороной и вершиной.
Рассмотрим примеры ответов смежных тупых углов. Представьте себе угол в форме буквы "L", где горизонтальная линия будет общей стороной, а вертикальная линия будет образовывать два тупых угла. Они будут смежными, так как обладают общей стороной и вершиной. Величина углов в этом случае будет больше 90 градусов, но меньше 180 градусов.
Могут ли смежные углы быть тупыми?

Острый угол - это угол, мера которого меньше 90 градусов. Тупой угол же имеет меру больше 90 градусов и меньше 180 градусов. Следовательно, смежные углы также могут быть тупыми.
Если угол АВС равен 120 градусам, а угол ВСD равен 100 градусам, то углы АВС и ВСD являются смежными и оба являются тупыми. Мера смежных углов может быть любой в пределах от 90 до 180 градусов.
Важно помнить, что общая сторона и общая вершина - это единственные условия для смежных углов, независимо от их типа. Таким образом, смежные углы могут быть как острыми, так и тупыми.
Знание о смежных углах и их свойствах помогает в решении различных задач и проблем связанных с геометрией. Поэтому важно хорошо изучить и понять это понятие.
Определение смежных углов и тупых углов
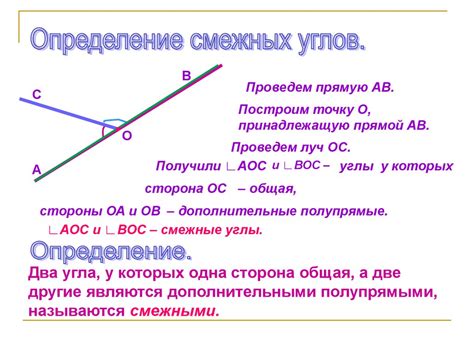
Тупой угол - это угол, мера которого превышает 90 градусов (но меньше 180 градусов). Тупой угол можно представить как угол, который "смотрит внутрь" фигуры. Например, угол в форме буквы "L" является тупым углом.
Смежные углы могут быть как острыми, так и тупыми. Например, если имеется два смежных угла и один из них - острый, а другой - тупой, то сумма этих углов будет равна 180 градусов. Это следует из определения линейных пар углов.
Например, у нас есть пара смежных углов: угол A и угол B. Угол A равен 60 градусов, и он является острым углом, а угол B равен 120 градусам и является тупым углом. Сумма этих углов равна 180 градусов.
Формула для проверки тупого угла

Смежные углы называются тупыми, если их сумма больше 180 градусов. Для проверки тупого угла между двумя линиями нужно использовать следующую формулу:
Угол 1 + угол 2 > 180 градусов
Если данное условие выполняется, то смежные углы являются тупыми. В противном случае, они не являются тупыми.
Например, у нас есть две линии, их смежные углы равны 100 градусов и 90 градусов. Подставляем значения в формулу:
Угол 1 + угол 2 > 180 градусов
100 градусов + 90 градусов > 180 градусов
190 градусов > 180 градусов
Так как условие выполняется, то смежные углы 100 градусов и 90 градусов являются тупыми.
Примеры из реальной жизни

Установка кухонной столешницы: при соединении двух столешниц образуется угол между ними. Если эти столешницы имеют прямоугольную форму и соединяются под прямым углом, то угол между ними будет тупым.
Расположение мебели в комнате: встречный угол между двумя смежными стенами может быть тупым. Например, если поверхность стены имеет форму треугольника, то встречный угол может быть больше 90 градусов.
Углы наклона на дорогах: при проектировании дорог часто возникают ситуации, когда необходимо создать поворот с большим углом. Это может быть место, где одна дорога пересекает другую под острым углом или поворот, который должен быть сделан с большой радиусной развязкой. В таких случаях смежные углы на дороге могут быть тупыми.
Эти примеры показывают, что смежные углы могут встречаться в различных ситуациях в реальной жизни и не ограничиваются только математическими задачами. Они являются частью нашего повседневного опыта и исполняют важные функции в архитектуре, дизайне и конструкции.
Геометрические модели смежных тупых углов
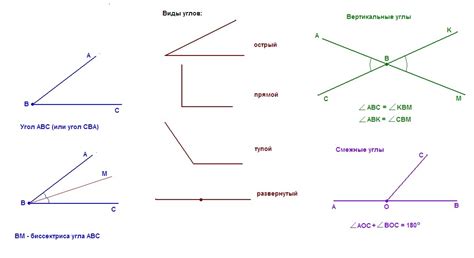
Модель №1. Расположение углов.
Допустим, у нас есть две прямые линии, пересекающиеся в точке O. На каждой линии выберем по две точки, A и B на первой линии, и C и D на второй. Если углы AOB и COD являются тупыми, то они являются смежными тупыми углами.
Модель №2. Отражение света.
Рассмотрим ситуацию, когда свет падает на два зеркала, расположенные под прямым углом друг к другу. Отраженный свет создает пару смежных углов. Если углы образуются при отражении света о зеркала являются тупыми, то они могут быть считаться смежными тупыми углами.
Модель №3. Складывание деталей.
Если у нас есть две детали, которые нужно сложить, при этом одна деталь имеет острую форму, а другая - тупую, то между ними образуется смежный тупой угол. Например, при сложении двух икосаэдров образуется смежный тупой угол.
Модель №4. Геометрические фигуры.
Смежные тупые углы могут образовываться при рассмотрении геометрических фигур. Например, если взять параллелограмм ABCD, а затем угол BCD сделать тупым, то угол ABC будет считаться смежным тупым углом.
Во всех этих моделях можно встретить смежные тупые углы, и они используются в геометрии и реальной жизни для различных вычислений и конструкций.
Значение смежных тупых углов в строительстве
Смежные тупые углы играют важную роль в строительстве и архитектуре. Они определяют форму и геометрию многих конструкций, позволяют оптимизировать использование материалов и создавать эстетически привлекательные объекты. Профессионалам в области строительства и архитектуры важно иметь понимание о значении и использовании смежных тупых углов.
Одним из примеров использования смежных тупых углов является проектирование крыш. Смежные тупые углы крыши помогают определить ее форму и угол наклона. В зависимости от желаемого стиля и функциональности здания, архитекторы могут использовать различные углы, чтобы создать уникальный внешний вид и обеспечить хорошую дренажную систему. Смежные тупые углы также могут определять этажность здания, угол наклона стен и другие конструктивные параметры.
Еще одним примером использования смежных тупых углов является проектирование оконных и дверных проемов. Архитекторы могут использовать тупые углы, чтобы создать интересную игру света и создать визуальные эффекты в помещении. Также смежные тупые углы позволяют определить соотношение размеров и пропорций окон и дверей в гармонии с общим стилем и дизайном здания.
В строительстве смежные тупые углы также важны для определения размещения и расстояния между перекрытиями и стенами. Они помогают балансировать нагрузки и обеспечивают прочность и устойчивость конструкции. Знание смежных тупых углов позволяет строителям оптимизировать использование материалов и создавать надежные и долговечные сооружения.
Ответы на часто задаваемые вопросы о смежных тупых углах

В этом разделе мы ответим на несколько часто задаваемых вопросов о смежных углах и рассмотрим примеры, демонстрирующие, что смежные углы могут быть тупыми.
Что такое смежные углы?
Смежные углы - это пара углов, которые имеют общую сторону и общую вершину, но не перекрываются.
Могут ли смежные углы быть тупыми?
Да, смежные углы могут быть как остроугольными, так и тупыми. Важно помнить, что острый угол имеет меньшее значение, чем прямой угол, а прямой угол имеет 90 градусов. Таким образом, смежные углы, образованные острыми углами, будут острыми углами, а смежные углы, образованные тупыми углами, будут тупыми углами.
Как найти меру смежных тупых углов?
Примеры смежных тупых углов
Пример 1:
В треугольнике ABC с углом C равным 120 градусов, угол B будет смежным тупым углом, так как его мера будет равна 180 - 120 = 60 градусов.
Пример 2:
В параллелограмме PQRS с углом R равным 135 градусов, угол S будет смежным тупым углом, так как его мера будет равна 180 - 135 = 45 градусов.
Доказательства смежности и тупости углов
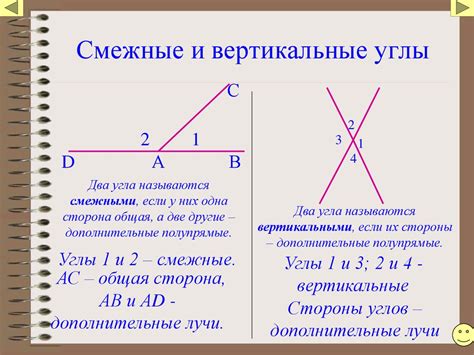
Доказательство с помощью прямой линии:
Допустим, у нас есть две прямые, пересекающиеся под определенным углом. Если мы проведем линию параллельно одной из прямых, которая пересекает другую прямую, то получим два смежных угла, которые будут тупыми.
Доказательство с помощью геометрических фигур:
Рассмотрим треугольник ABC, в котором угол BAC равен 90 градусам. Мы можем провести перпендикуляр к стороне BC, проходящий через точку A. Таким образом, получаем два смежных угла - угол BAC и угол BCA, которые будут тупыми.
Доказательство с помощью свойств углов:
Известно, что сумма углов в треугольнике равна 180 градусам. Рассмотрим треугольник ABC, в котором угол ABC равен 120 градусам. Из суммы углов треугольника следует, что углы BAC и BCA должны быть тупыми.
Вышеуказанные доказательства позволяют установить факт смежности и тупости углов в различных геометрических ситуациях. Знание этих доказательств может быть полезно при решении задач и построении геометрических конструкций.