Трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна. Эта геометрическая фигура имеет множество интересных свойств и характеристик, одна из которых – это её стороны. Стоит отметить, что важную роль в определении сторон трапеции играют параллельные плоскости.
Первая пара параллельных сторон трапеции называется основаниями. Они лежат на плоскостях, которые называются боковыми. Основания могут быть разной длины, и длина каждого из них является основательным параметром для определения размеров и свойств трапеции в целом.
Вторая пара сторон трапеции называется боковыми сторонами. Её длина и угол наклона относительно оснований также определяют форму и размеры трапеции. Боковые стороны трапеции могут быть параллельными друг другу, так как они лежат на параллельных плоскостях.
Итак, параллельные плоскости и их взаимодействие с основаниями и боковыми сторонами трапеции играют ключевую роль в определении формы и размеров этой геометрической фигуры. Изучение этих характеристик помогает понять связь между сторонами трапеции и её геометрическими свойствами, и раскрыть ещё больше тайн и тонкостей мира геометрии.
Определение и основные характеристики трапеции
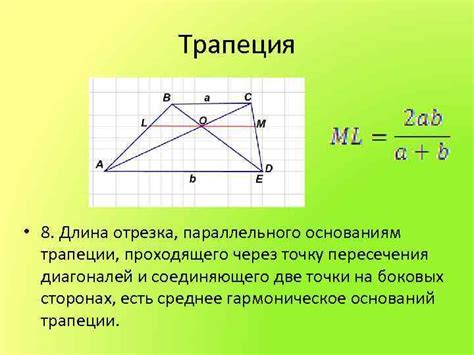
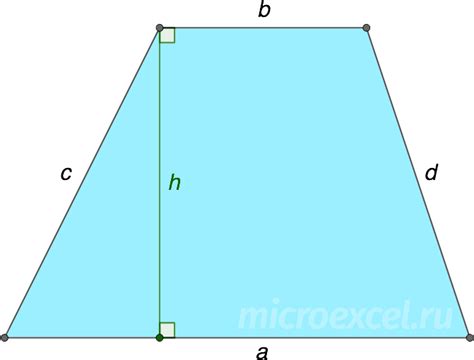
Основания трапеции – это параллельные стороны, которые определяют ее форму и размер. Обозначим их как a и b. Высота трапеции – это расстояние между ее основаниями. Она обозначается как h.
Боковые стороны трапеции – это сегменты, соединяющие основания и образующие углы с ними. Обозначим их как c и d. Сумма длин боковых сторон равна периметру трапеции.
Трапеция имеет два основных угла – прямой угол между основаниями и угол между одним из оснований и боковой стороной. Они обозначаются как α и β соответственно.
В зависимости от соотношения длин оснований, трапеции подразделяются на равнобедренные и произвольные. В равнобедренной трапеции длины боковых сторон и углы между ними равны, а высота является медианой. В произвольной трапеции эти характеристики могут быть разными.
Различные типы трапеций и их свойства
- Прямоугольная трапеция: у этого типа трапеции одна пара сторон параллельна и перпендикулярна другой паре, а углы между непараллельными сторонами равны 90 градусов.
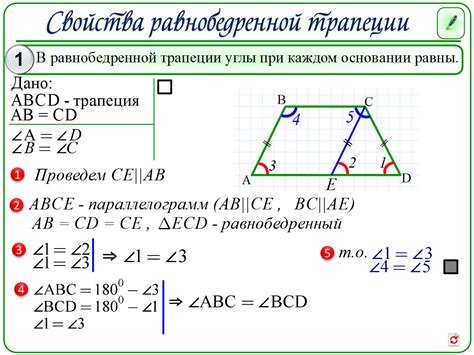
- Равнобедренная трапеция: у этого типа трапеции две стороны равны, а углы между ними также равны.
- Равносторонняя трапеция: у этой трапеции все стороны равны, а углы между ними равны 60 градусов.
- Произвольная трапеция: это любой четырехугольник, у которого хотя бы две стороны параллельны друг другу.
Все трапеции имеют несколько общих свойств:
- Сумма всех внутренних углов трапеции равна 360 градусов.
- Биссектриса угла между параллельными сторонами делит диагональ, соединяющую основания трапеции, на две равные части.
- Периметр трапеции вычисляется по формуле: P = a + b + c + d, где a, b, c и d - длины сторон.
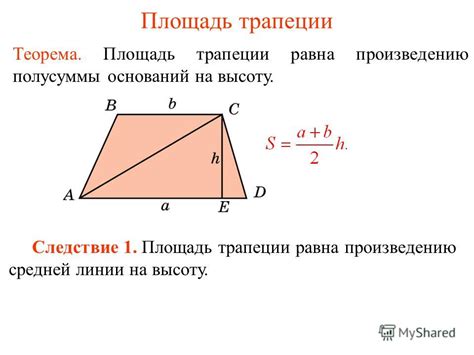
- Площадь трапеции вычисляется по формуле: S = ((a + b) * h) / 2, где a и b - длины оснований, а h - высота трапеции.
Различные типы трапеций имеют разные свойства и могут применяться в разных математических и геометрических задачах. Изучение этих свойств помогает лучше понять структуру и особенности этого важного геометрического объекта.
Концепция параллельных плоскостей в геометрии

В геометрии параллельные плоскости представляют собой особый класс плоскостей, которые никогда не пересекаются, независимо от своего расположения в пространстве. Это важное понятие, которое находит широкое применение в различных областях, таких как архитектура, инженерия и физика.
Для того чтобы понять, что плоскости являются параллельными, необходимо учесть следующие характеристики:
- Параллельные плоскости имеют одинаковое направление. Это значит, что все прямые линии, параллельные одной плоскости, также будут параллельны и другой.
- Параллельные плоскости не пересекаются во всем пространстве. Если бы они имели общую точку пересечения, то они уже не были бы параллельными.
- Параллельные плоскости могут быть сдвинуты друг относительно друга, но сохраняют свою параллельность.
Параллельные плоскости имеют важные свойства и особенности. Например, они позволяют нам строить параллельные линии, измерять расстояние между плоскостями и решать задачи, связанные с пересечением плоскостей.
В геометрии трапеции, знание понятия параллельных плоскостей играет важную роль при анализе сторон трапеции. Параллельность оснований и боковых сторон определяет свойства и взаимное расположение элементов трапеции.
Взаимосвязь между сторонами трапеции и плоскостями
Основное свойство трапеции - параллельность одной пары ее сторон. В связи с этим параллельность сторон трапеции находит отражение в поведении плоскостей, которые определяют этот четырехугольник.
Когда мы строим трапецию, мы задаем плоскости, которые образуют ее стороны. Плоскость, образующая одну пару параллельных сторон, называется базовой плоскостью. Она задает основание трапеции.
Другая пара параллельных сторон трапеции образуют боковые плоскости. Они определены прямыми, соединяющими соответствующие вершины трапеции.
Взаимосвязь между сторонами трапеции и плоскостями проявляется в том, что каждая сторона трапеции лежит в одной из плоскостей, определяющих этот четырехугольник. Параллельность одной пары сторон обусловлена параллельностью соответствующих базовой и боковых плоскостей.
Таким образом, стороны трапеции и плоскости, образующие этот четырехугольник, взаимосвязаны и взаимоопределены друг относительно друга. Понимание этой взаимосвязи позволяет более глубоко изучить свойства и характеристики трапеции, а также применять их в практических задачах и решениях.
Анализ геометрических пропорций и симметрии на примере трапеции
Пропорции трапеции могут быть выражены с помощью соотношения длин ее сторон. В частности, можно выделить следующие соотношения:
- Отношение оснований: Длина одной основания трапеции (a) к длине другой основания (b) определяет основание t и равно a:b=t.
- Отношение боковых сторон: Длина одной боковой стороны трапеции (c) к длине другой боковой стороны (d) также имеет свое соотношение, равное c:d=s.
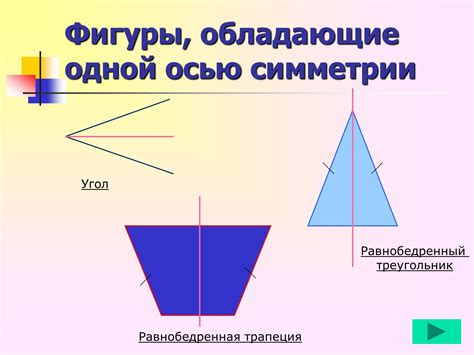
Геометрическая симметрия трапеции проявляется в нескольких аспектах:
- Органичение: Основания трапеции параллельны и одинаковой длины, что создает горизонтальную симметрию. Таким образом, отношение a:b=t=1, a=b.
- Дополнение: Боковые стороны трапеции не параллельны и отличаются длиной. Это создает вертикальную симметрию и отношение c:d=s=1, c=d.
Анализ геометрических пропорций и симметрии трапеции позволяет лучше понять ее структуру и свойства. Это знание является основой для решения различных задач, связанных с трапециями, а также для построения более сложных геометрических фигур.
Сферическая геометрия и ее значения для изучения сторон трапеции
Изучение сторон трапеции с помощью сферической геометрии имеет несколько значений. Первое значение заключается в описании геометрических свойств трапеции на поверхности сферы. Такая трапеция называется сферической трапецией и имеет боковые стороны, соединяющие две точки на сфере, а также две дуговые стороны, соединяющие эти точки.
Второе значение состоит в определении связей между сторонами сферической трапеции и другими параметрами, такими как углы и расстояния на сфере. Например, можно изучать взаимосвязь между длиной дуговых сторон и углом между ними, или между длиной боковых сторон и углом, образуемым ими с полюсом сферы.
Третье значение сферической геометрии для изучения сторон трапеции связано с приложениями в реальной жизни. Например, сферическая геометрия может использоваться при расчете пути полета спутников или при определении местоположения объектов на поверхности Земли с помощью геодезических сетей.
Использование сферической геометрии для изучения сторон трапеции позволяет более полно описывать и анализировать особенности этой фигуры на поверхности сферы. Это может быть полезно для решения практических задач, связанных с геометрией и измерениями на сферических объектах.
| Термин | Описание |
|---|---|
| Сферическая трапеция | Трапеция на поверхности сферы, имеющая боковые стороны и дуговые стороны |
| Угол между дуговыми сторонами | Угол, образуемый двумя дуговыми сторонами сферической трапеции |
| Угол между боковыми сторонами и полюсом | Угол, образуемый боковыми сторонами сферической трапеции и линией, соединяющей полюс сферы с ее центром |
Значимость понимания сторон трапеции для решения практических задач
Первое, что следует учитывать при решении практических задач, связанных с трапециями, это основа и боковые стороны. Основа трапеции - это боковые стороны, которые лежат на параллельных плоскостях. Знание и понимание основы позволяют определить геометрические параметры трапеции, такие как площадь и периметр. Например, для вычисления площади трапеции необходимо знать длины основы и высоту. Также, основа и боковые стороны используются для измерения углов и определения основных свойств трапеции.
Другой важной стороной трапеции является диагональ. Знание длин диагоналей позволяет решить задачи, связанные с построением трапеции, определением ее формы и положения в пространстве. В практическом применении, диагонали могут быть использованы для определения дополнительных свойств трапеции, таких как ее центральная симметричность, осевая симметричность и др.
Также, стороны трапеции являются основой для расчетов и анализа трапециевидных фигур в различных областях, таких как архитектура, геодезия, строительство, графика и дизайн. Знание и понимание сторон трапеции существенно помогает в определении геометрических параметров, установлении пропорций и создании правильных изображений трапецевидных объектов.
В итоге, понимание сторон трапеции имеет ценность не только с точки зрения математической теории, но и в практической деятельности. Оно позволяет решать различные задачи, связанные с этой геометрической фигурой, и применять полученные знания в различных областях деятельности. Поэтому, освоение основ трапеции является важным шагом в развитии математических навыков и практического мышления.