Найти сумму делителей числа - задача, с которой сталкиваются многие математики и программисты. Однако, даже опытные специалисты иногда допускают ошибки, что может привести к неправильным результатам и неполадкам в программном коде.
В данной статье мы рассмотрим гарантированный метод, который позволяет найти сумму делителей числа без каких-либо ошибок. Этот метод основан на простом, но эффективном подходе, который можно применять для любого числа.
Основная идея заключается в том, чтобы перебрать все числа от 1 до половины данного числа и проверить, является ли оно делителем. Если число является делителем, то оно добавляется к сумме. Таким образом, мы гарантированно получим правильную сумму всех делителей числа.
Применив этот метод, вы сможете избежать возникновения ошибок и получить точный результат. Это особенно важно при разработке программного кода, где неправильное нахождение суммы делителей может привести к некорректной работе программы или непредсказуемому поведению.
Используйте гарантированный метод для нахождения суммы делителей числа и уверенно приступайте к решению сложных задач, связанных с математикой и программированием!
Что такое сумма делителей числа?

Для примера, пусть задано число 12. Делители этого числа: 1, 2, 3, 4, 6 и 12. Сумма делителей будет равна 1 + 2 + 3 + 4 + 6 + 12 = 28.
Сумма делителей может быть полезна в различных математических задачах и алгоритмах, таких как поиск совершенных чисел, проверка на простоту числа и других.
Для вычисления суммы делителей числа существуют различные методы и алгоритмы, включая гарантированный метод, который обеспечивает точность вычислений и исключает возможность ошибок.
Метод поиска суммы делителей числа

Для нахождения суммы делителей числа нужно разложить его на простые множители. Затем нужно воспользоваться формулой:
Сумма делителей числа равна произведению всех степеней его простых множителей, увеличенному на единицу, разделенному на произведение самих простых множителей, уменьшенное на единицу.
Это математическое выражение можно записать следующим образом:
S = (p1i1 + 1)(p2i2 + 1)...(pnin + 1) / (p1 - 1)(p2 - 1)...(pn - 1)
Где p1, p2,..., pn - простые множители числа, а i1, i2,..., in - степени этих множителей.
Таким образом, чтобы найти сумму делителей числа, необходимо найти его простые множители и степени этих множителей, а затем использовать данную формулу.
Этот метод позволяет гарантированно и без ошибок найти сумму делителей числа.
Простейший способ нахождения суммы делителей числа

Для нахождения суммы всех делителей числа без ошибок можно использовать простейший метод. В этом методе мы перебираем все числа от 1 до самого числа и проверяем, делится ли оно наше число без остатка. Если делится, то мы прибавляем это число к сумме делителей. В конце мы получаем искомую сумму.
Например, для числа 6 делителями будут числа 1, 2, 3 и 6. Мы перебираем все числа от 1 до 6 и прибавляем к сумме только числа, которые делятся на 6 без остатка. В итоге получаем сумму делителей равной 1 + 2 + 3 + 6 = 12.
Таким образом, простейший способ нахождения суммы делителей числа позволяет получить точный результат без ошибок и итераций. Этот метод может быть использован для любых чисел без ограничений.
Алгоритм нахождения суммы делителей числа
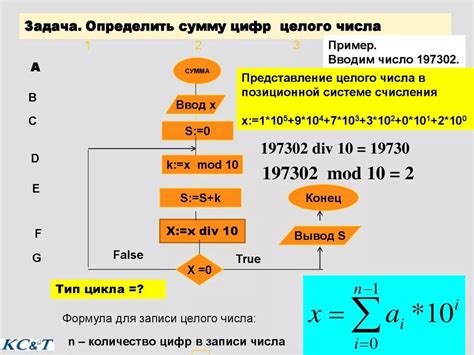
Для того чтобы найти сумму делителей числа, можно использовать следующий алгоритм:
- Инициализировать переменную sum и присвоить ей значение 0.
- Пройти циклом от 1 до числа, для каждого числа проверить, делится ли оно на исходное число без остатка.
- Если делится, то добавить это число к переменной sum.
- После завершения цикла, переменная sum будет содержать сумму делителей числа.
Пример:
```
int number = 12;
int sum = 0;
for (int i = 1; i <= number; i++) {
if (number % i == 0) {
sum += i;
}
}
System.out.println("Сумма делителей числа " + number + " равна " + sum);
``` В результате выполнения указанного алгоритма для числа 12, будет найдена сумма делителей, которая равна 28. Таким образом, данный метод позволяет найти сумму делителей числа без ошибок и достаточно эффективно.
Гарантированный метод нахождения суммы делителей числа

Для нахождения суммы делителей числа существует гарантированный метод, который не содержит ошибок и позволяет получить точный результат. Этот метод основан на простом алгоритме подсчета делителей и их последующем суммировании.
Прежде всего, необходимо разложить число на простые множители. Для этого применяется алгоритм деления числа на наименьшие простые числа, начиная с 2. Каждый раз, когда число делится без остатка на простое число, оно заменяется на результат деления, а найденное простое число добавляется в список множителей. Этот процесс продолжается до тех пор, пока число не станет равным 1. Полученные простые множители составляют основу для дальнейших вычислений.
Далее необходимо найти все положительные целочисленные степени каждого простого множителя. Для этого проходимся по всем простым множителям и подсчитываем степени, начиная с 0 и до максимальной степени, при которой значение степени простого множителя не превышает само число. Полученные значения степеней также добавляются в список.
Теперь можно приступить к вычислению суммы делителей. Для этого необходимо использовать формулу, которая основывается на свойствах степеней, простых множителей и суммы геометрической прогрессии. Формула выглядит следующим образом:
- Для простого множителя p и его степени a: сумма делителей равна (p^(a+1) - 1) / (p - 1)
Таким образом, чтобы найти сумму делителей числа, необходимо применить эту формулу к каждому простому множителю и его степени, а затем сложить полученные значения для всех простых множителей.
Итак, гарантированный метод нахождения суммы делителей числа состоит из нескольких шагов: разложение числа на простые множители, подсчет степеней простых множителей, применение формулы и сложение полученных значений. Такой подход обеспечивает точный результат и позволяет избежать ошибок при вычислении суммы делителей.
Формула для вычисления суммы делителей числа

Сумма делителей числа может быть вычислена с помощью специальной формулы, которая позволяет получить точный результат без необходимости перебирать все делители числа:
- Найдите простые множители числа. Для этого можно использовать метод факторизации числа.
- Вычислите степени простых множителей, возведенные в степень на один больше, и вычислите их произведение. Это можно сделать с помощью формулы σ(n) = (p_1^(a_1+1) - 1) / (p_1 - 1) * (p_2^(a_2+1) - 1) / (p_2 - 1) * ... * (p_k^(a_k+1) - 1) / (p_k - 1), где p_i - простой множитель, a_i - степень простого множителя.
- Получите сумму делителей числа, используя полученное произведение.
Например, для числа 12 простые множители - 2 и 3. Степени этих множителей равны 2 и 1. По формуле получаем: σ(12) = (2^3 - 1) / (2 - 1) * (3^2 - 1) / (3 - 1) = (8 - 1) / 1 * (9 - 1) / 2 = 7 * 4 = 28. Таким образом, сумма делителей числа 12 равна 28.
Такой способ вычисления суммы делителей числа позволяет получать результаты быстро и точно, что делает его предпочтительным при решении подобных задач.
Специальные случаи нахождения суммы делителей числа

При вычислении суммы делителей числа могут возникать некоторые специальные случаи, которые имеет смысл учесть:
- Когда число является простым, то есть имеет только два делителя - 1 и само число. В этом случае сумма делителей равна сумме этих двух чисел и равна самому числу.
- Когда число равно 1, то единственным его делителем является само число 1, поэтому сумма делителей равна 1.
- Когда число равно 0, то делителями не является ни одно другое число, поэтому сумма делителей также равна 0.
Такие специальные случаи можно учесть при написании алгоритма нахождения суммы делителей числа, чтобы избежать ошибок и учесть все возможные ситуации.
| Число | Сумма делителей |
|---|---|
| 2 | 3 |
| 11 | 12 |
| 1 | 1 |
| 0 | 0 |
В таблице приведены примеры вычислениясуммы делителей для различных чисел, включая простые числа, единицу и ноль. Обратите внимание, что сумма делителей простых чисел равна сумме числа и единицы, в то время как для числа 1 и 0 сумма делителей равна самому числу.