Некоторые математические задачи кажутся сложными и требуют использования формул и специальных инструментов. Однако, существуют способы решения таких задач без использования формул и калькуляторов. Например, диагональ квадрата может быть найдена с помощью простых геометрических принципов.

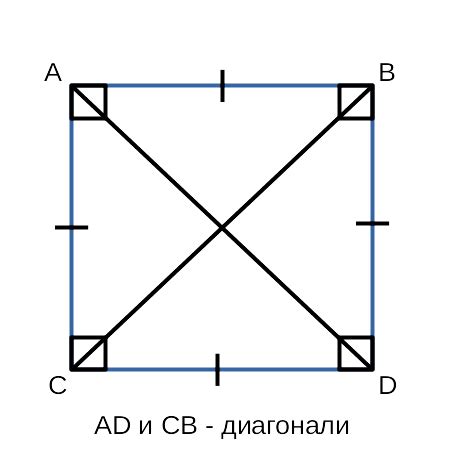
Сначала, важно понять, что диагональ квадрата - это отрезок, соединяющий две противоположные вершины квадрата. Данный отрезок является самой длинной стороной квадрата и делит его на два прямоугольных треугольника.

Для того чтобы найти диагональ квадрата без формул и калькулятора, можно воспользоваться прямоугольным треугольником. По теореме Пифагора известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. В данном случае, гипотенузой является диагональ квадрата, а катетами - его стороны.

Определение диагонали квадрата

Метод 1: Использование теоремы Пифагора

Для нахождения длины диагонали квадрата можно воспользоваться теоремой Пифагора. Если известна длина стороны квадрата (a), можно выразить длину диагонали (d) следующим образом:

d = a√2

Где √2 - корень из 2 (приближенное значение равно 1.414).

Например, если сторона квадрата равна 10 см, диагональ будет равна:

d = 10√2 ≈ 10*1.414 ≈ 14.142 см

Метод 2: Использование свойств равнобедренного треугольника

Квадрат является особым случаем равнобедренного треугольника, у которого все стороны равны. Поэтому, длина диагонали может быть выразена через формулу:

d = a√2/2

Например, если сторона квадрата равна 10 см, диагональ будет равна:

d = 10√2/2 ≈ 10*1.414/2 ≈ 7.071 см

Оба этих метода позволяют определить длину диагонали квадрата без использования формул и калькулятора. На практике можно использовать любой из них в зависимости от удобства и доступности конкретных данных.

Простой способ без формул и калькулятора

Найдите значение стороны квадрата, например, измерьте ее длину с помощью линейки. После этого умножьте полученную длину на √2. Результатом будет значение диагонали данного квадрата.

Например, если сторона квадрата равна 10 см, то диагональ будет равна 10 см * √2 ≈ 14,14 см.

Этот метод основан на связи сторон квадрата и его диагонали. Зная длину одной стороны, мы можем найти длину диагонали с помощью простых математических операций без использования сложных формул или калькулятора.

Методика нахождения длины диагонали квадрата

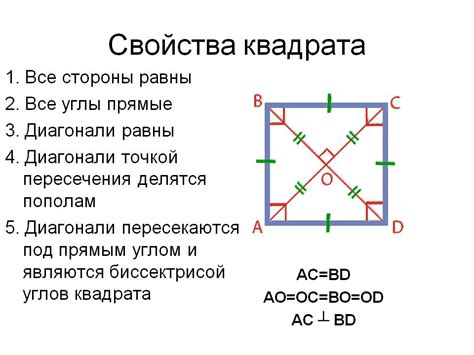
Существуют различные методики для нахождения длины диагонали квадрата, но один из самых простых и понятных методов направлен на использование свойств прямоугольного треугольника. Ведь диагональ квадрата образует прямоугольный треугольник с его сторонами.

1. Возьмите сторону квадрата и обозначьте ее длину как a.
2. Используя теорему Пифагора, найдите длину диагонали квадрата (d) через сторону (a) по формуле: d = a * √2.

Таким образом, длина диагонали квадрата равна произведению длины одной его стороны на корень из двух.

Применение этой методики позволяет без использования формул и калькулятора определить длину диагонали квадрата, что может быть полезным при решении различных задач геометрии или при оценке размеров объектов, основанных на форме квадрата.

Понятное объяснение в нескольких шагах

Чтобы найти диагональ квадрата без использования формул и калькулятора, можно следовать нескольким простым шагам:

1. Найдите длину стороны квадрата. Для этого можно взять рулетку или линейку и измерить одну из сторон квадрата.
2. Умножьте длину стороны на корень из 2. Для этого нужно умножить значение длины на примерно 1,4142 (округленное значение корня из 2).
3. Округлите полученное значение до нужного количества десятичных знаков (если требуется).

Теперь у вас есть значение диагонали квадрата. Обратите внимание, что эти шаги демонстрируют простой метод расчета диагонали и носят информационный характер. Для точного результата рекомендуется использовать формулу d = a * √2, где d - диагональ, a - сторона квадрата.

Практическое использование полученного результата

Зная значение диагонали квадрата, вы можете применять его в различных практических ситуациях.

Например, представьте, что вам нужно построить квадратное озеро в саду и вы хотите знать, какова должна быть длина каждой стороны, чтобы озеро имело желаемый размер.

Вы можете использовать полученную диагональ для расчета длины стороны квадрата. Примените связь между длиной диагонали и длиной стороны, а именно, что длина диагонали квадрата равна √2 (корень из 2) умноженный на длину его стороны.

Таким образом, если известна длина диагонали, вы можете найти длину стороны квадрата, разделив длину диагонали на √2 (приближенно 1,414).

Также, зная длину диагонали, вы можете использовать ее для расчета площади квадрата. Поскольку каждая сторона квадрата равна длине диагонали, вы можете умножить длину диагонали на саму себя и разделить на 2, чтобы получить площадь квадрата.

Вот несколько примеров практического использования полученного результата. Ознакомившись с основами поиска диагонали квадрата, вы можете применять эти знания в различных сферах.