Трапеция – это геометрическая фигура, которая имеет две параллельные стороны и две непараллельные стороны (основания). Важной характеристикой трапеции является ее периметр, который представляет собой сумму длин всех ее сторон. Нахождение периметра трапеции – это одно из основных заданий в геометрии, которое требует знания соответствующей формулы и умения ее применить.
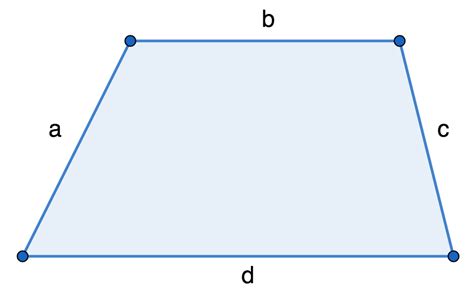
Формула для расчета периметра трапеции включает в себя сумму длин всех ее сторон. Периметр обычно обозначается символом P. Для трапеции с основаниями a и b, а также боковыми сторонами c и d формула будет выглядеть следующим образом:
P = a + b + c + d
Теперь, когда у нас есть формула для расчета периметра трапеции, давайте рассмотрим несколько примеров, чтобы лучше понять, как применять эту формулу на практике.
Что такое периметр трапеции?

Формула для расчета периметра трапеции: P = a + b1 + b2 + c, где P - периметр, a - длина одного из оснований, b1 и b2 - длины боковых сторон, c - разность длин оснований.
Для примера, рассмотрим трапецию с основаниями длиной 8 см и 12 см, а боковыми сторонами длиной 6 см и 4 см. Чтобы найти периметр, мы должны сложить длины всех сторон: 8 + 12 + 6 + 4 = 30 см. Таким образом, периметр этой трапеции равен 30 см.
Определение и формула для расчета периметра трапеции

Для расчета периметра трапеции существует универсальная формула:
Периметр = a + b + c + d, где:
- a - длина одной параллельной стороны
- b - длина другой параллельной стороны
- c и d - длины непараллельных сторон
Для примера рассмотрим трапецию со следующими сторонами:
- a = 5 см
- b = 7 см
- c = 4 см
- d = 6 см
Для вычисления периметра подставим значения в формулу:
Периметр = 5 + 7 + 4 + 6 = 22 см
Таким образом, периметр данной трапеции составляет 22 см.
Как найти периметр трапеции по известным значениям сторон?

Формула для нахождения периметра трапеции по известным значениям сторон:
Периметр = a + b + c + d
где:
- a, b – это длины параллельных сторон трапеции;
- c, d – это длины непараллельных сторон трапеции.
Например, если длина основания трапеции a = 5 см, длина верхнего основания b = 8 см, длина боковых сторон c = 6 см и d = 4 см, то периметр трапеции можно найти следующим образом:
- Периметр = 5 + 8 + 6 + 4 = 23 см.
Таким образом, периметр трапеции по заданным значениям сторон равен 23 см.
Примеры расчета периметра трапеции
Для вычисления периметра трапеции необходимо знать длины ее сторон или диагоналей. Рассмотрим несколько примеров расчета периметра трапеции:
Пример 1:
Дана трапеция со сторонами a = 5 см, b = 7 см и диагоналей d₁ = 4 см, d₂ = 6 см.
Сначала найдем длину боковой стороны c:
c = −√(d₁² − ((b - a + d₂)² − d₂²) / (2∙(b - a + d₂))) = −√(4² - ((7 - 5 + 6)² − 6²) / (2∙(7 - 5 + 6))) = −√(16 - ((8)² − 6²) / (2∙8)) = −√(16 - (64 - 36) / 16) = −√(16 - 28 / 16) = −√(16 - 1.75) = −√(14.25) ≈ −3.77 см
Так как длина стороны не может быть отрицательной, то результат отрицательный и не подходит для данной задачи.
Теперь найдем периметр трапеции:
P = a + b + c + d₁ + d₂ = 5 + 7 + 3.77 + 4 + 6 ≈ 25.77 см
Пример 2:
Дана трапеция со сторонами a = 10 мм, b = 15 мм и диагональю d₁ = 12 мм.
Сначала найдем длину боковой стороны c:
c = −√(d₁² − ((b - a)²) / 4) = −√(12² − ((15 - 10)²) / 4) = −√(144 - 25 / 4) = −√(144 - 6.25) = −√(137.75) ≈ −11.73 мм
Так как длина стороны не может быть отрицательной, то результат отрицательный и не подходит для данной задачи.
Теперь найдем периметр трапеции:
P = a + b + c + d₁ = 10 + 15 + 11.73 + 12 ≈ 48.73 мм
Пример 3:
Дана трапеция со стороной a = 6 см, боковой стороной c = 8 см и диагоналями d₁ = 5 см, d₂ = 7 см.
Так как значения сторон и диагоналей уже известны, просто выполняем сложение:
P = a + b + c + d₁ + d₂ = 6 + b + 8 + 5 + 7 = 26 + b
Таким образом, периметр трапеции равен 26 + b.
Это были несколько примеров расчета периметра трапеции. Не забывайте, что для правильного решения задачи необходимо обладать знаниями формулы для нахождения периметра и сторон или диагоналей трапеции.