Физика – это одна из основных наук, которая изучает законы природы и объясняет, как все вокруг нас работает. Одним из наиболее интересных и полезных аспектов физики является изучение перемещения. На протяжении многих веков ученые и гениальные умы пытались выяснить, как предсказать и определить путь перемещения тела.
Одной из основных концепций, лежащих в основе физики движения, является принцип инерции. Этот принцип выражает идею, что тела сохраняют свое состояние покоя или постоянного прямолинейного движения, пока на них не действуют внешние силы. Однако, когда на тело действует внешняя сила, оно начинает перемещаться и следовать определенному пути.
Чтобы определить путь перемещения тела, физики разработали различные формулы и уравнения, которые основываются на законах Ньютона. Например, одно из основных уравнений для определения пути движения тела в одномерном пространстве – это уравнение движения:
s = ut + (1/2)at^2
Где s – путь перемещения, u – начальная скорость, t – время, a – ускорение. Эта формула позволяет вычислить, какой путь пройдет тело за определенное время при определенной начальной скорости и ускорении.
Физика движения: основные принципы и формулы
Основными принципами физики движения являются:
- Принцип инерции - тело находится в состоянии покоя или равномерного прямолинейного движения, пока на него не действует внешняя сила.
- Принцип сохранения импульса - в изолированной системе сумма импульсов тел остается неизменной.
- Принцип сохранения энергии - в изолированной системе полная энергия остается постоянной, то есть может изменяться только форма энергии.
Для описания движения тел используются формулы физики. Некоторые основные формулы физики движения:
- Скорость (v) - величина, равная отношению пройденного пути (s) к интервалу времени (t): v = s / t.
- Ускорение (a) - изменение скорости со временем: a = (v2 - v1) / t.
- Движение равноускоренное - движение, при котором ускорение постоянно: s = v0 * t + (a * t^2) / 2.
- Движение прямолинейное равномерное - движение со скоростью, не изменяющейся со временем: s = v * t.
Знание основных принципов и формул физики движения позволяет предсказывать и объяснять движение тел в различных ситуациях. Оно является основой для понимания многих явлений и процессов в мире окружающей нас физической реальности.
Относительность движения и пространственная координата
Пространственная координата играет важную роль в определении пути перемещения объекта. Она позволяет нам установить местоположение объекта в пространстве на основе его относительного положения относительно других объектов или точек отсчета.
Пространственная координата может быть одномерной, двумерной или трехмерной, в зависимости от количества измерений, необходимых для определения положения объекта. В одномерной системе координат положение объекта может быть определено лишь по одной оси, например, по оси X. В двумерной системе координат положение объекта определяется по двум осям, например, по осям X и Y. А в трехмерной системе координат положение объекта определяется по трём осям – X, Y и Z.
Относительность движения и пространственная координата объединяются в единую концепцию, позволяющую нам более полно и точно описывать и предсказывать путь перемещения объектов, а также изучать законы и принципы, которыми они руководствуются.
Пример:
Рассмотрим движение автомобиля по прямой трассе. Автомобиль движется от точки А до точки Б со скоростью 60 км/ч. В данном случае, точка А может рассматриваться как начальная точка отсчета, и пространственная координата будет описывать положение автомобиля на трассе относительно данной точки. Точка Б, в свою очередь, будет конечной точкой.
Используя относительность движения и пространственную координату, мы можем определить точку, в которой автомобиль находится в определенный момент времени, а также предсказать время, необходимое для достижения конечной точки. Это является основой для решения широкого спектра задач в физике, инженерии и других науках.
Важно понимать, что относительность движения и пространственная координата тесно связаны друг с другом и вместе образуют основу для изучения и понимания перемещения объектов в пространстве.
Начальная скорость и изменение положения

Начальная скорость - это скорость объекта в момент начала движения. Она определяется вектором, который указывает направление и величину скорости. Однако, для простоты расчетов, обычно используется одномерное движение, где направление скорости нам не важно.
Изменение положения - это разница между конечной и начальной позицией объекта. Оно также может быть представлено вектором, где величина вектора равна модулю разности позиций, а направление указывает на направление движения.
Формула для вычисления изменения положения объекта при известной начальной скорости и времени движения выглядит следующим образом:
| Формула | Описание |
|---|---|
| Δx = v0 * t | Изменение положения (Δx) равно произведению начальной скорости (v0) на время движения (t) |
Где:
- Δx - изменение положения
- v0 - начальная скорость
- t - время движения
Эта формула применяется для одномерного движения, где скорость остается постоянной. Если скорость изменяется, то необходимо использовать другие формулы и учитывать дополнительные факторы в расчетах.
Начальная скорость и изменение положения играют важную роль в физике, позволяя нам анализировать движение объектов и предсказывать их будущие положения. Они помогают нам понять, как движение происходит и как оно может измениться в зависимости от различных факторов.
Скорость и ускорение: взаимосвязь и формулы

Скорость обозначается буквой v, а ускорение - буквой a. Для расчета скорости и ускорения используются специальные формулы.
Формула для расчета скорости выглядит следующим образом:
v = s/t
где s - пройденный путь, а t - время, за которое путь был пройден. Скорость измеряется в единицах длины, например, метрах в секунду.
Ускорение также можно рассчитать при помощи формулы:
a = (v - u)/t
где u - начальная скорость, а t - время. Здесь ускорение измеряется в единицах длины за единицу времени в квадрате, например, метрах в секунду в квадрате.
Скорость и ускорение являются взаимосвязанными величинами: ускорение показывает, как быстро скорость изменяется со временем. Если ускорение положительно, то скорость увеличивается, а если ускорение отрицательно, то скорость уменьшается.
Обратите внимание, что величина ускорения также может быть постоянной величиной, если его значение не меняется в течение времени.
Знание формул скорости и ускорения позволяет более точно описывать движение тела и рассчитывать его характеристики, такие как временной интервал, пройденный путь или изменение скорости в процессе движения.
Силы и равнодействующая сила
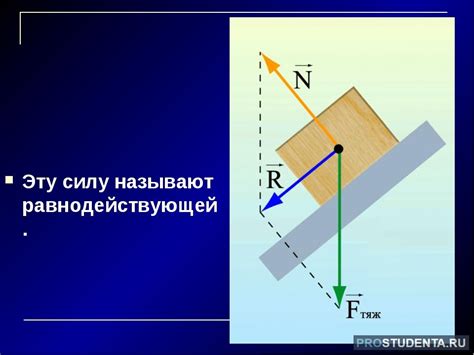
Силы могут быть разных типов: сила тяжести, сила трения, электростатические и магнитные силы и другие. Каждая из них имеет свои особенности и расчетные формулы.
Однако, при взаимодействии нескольких сил на объект, важно знать их равнодействующую силу. Равнодействующая сила - это сумма всех сил, действующих на объект в заданном направлении. Она может быть определена как величина и направление.
Чтобы найти равнодействующую силу, нужно сложить все воздействующие силы векторным способом. Векторное сложение сил осуществляется по правилу параллелограмма или по правилу треугольника.
При изучении перемещения объекта важно учитывать равнодействующую силу, так как она определяет его скорость и ускорение. Знание равнодействующей силы позволяет предсказать путь перемещения объекта под ее воздействием.
Ручное вычисление равнодействующей силы может быть сложным, поэтому существуют специальные формулы и методы расчета, которые помогают упростить эту задачу.
Силы и равнодействующая сила играют важную роль в изучении перемещения и движения объектов. Понимание их принципов позволяет предсказывать и объяснять различные физические явления.
Законы Ньютона и применение в различных ситуациях
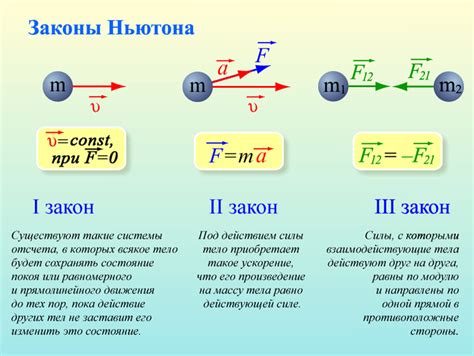
Первый закон Ньютона, также известный как закон инерции, утверждает, что тело сохраняет свое состояние покоя или равномерного прямолинейного движения, если на него не действуют внешние силы. Этот закон позволяет объяснить, почему тело остается в покое или продолжает двигаться равномерно, пока на него не начнут действовать силы.
Пример применения первого закона Ньютона: Если тело находится в состоянии покоя на горизонтальной поверхности и на него не действуют внешние силы, оно останется в покое. Однако, если на тело начнет действовать сила, например, приложенная рука, оно начнет двигаться в направлении этой силы.
Второй закон Ньютона, также известный как закон движения, формулирует прямую связь между силой, массой тела и его ускорением. Согласно второму закону, ускорение тела пропорционально силе, действующей на него, и обратно пропорционально его массе.
Пример применения второго закона Ньютона: Если на тело массой 2 кг действует сила 10 Н, то его ускорение можно рассчитать по формуле: а = F/m = 10/2 = 5 м/с². То есть, тело будет ускоряться со скоростью 5 м/с² в направлении силы.
Третий закон Ньютона, также известный как закон взаимодействия, утверждает, что каждое действие сопровождается равным по модулю, противоположно направленным воздействием. Силы всегда действуют парами, и приложенная к одному телу сила вызывает равную по модулю, но противоположно направленную силу на другом теле.
Пример применения третьего закона Ньютона: Когда две телеги соударяются друг с другом, они оказывают на друг друга равные по модулю, но противоположно направленные силы. Если одна телега действует на другую с силой 50 Н вперед, другая телега оказывает на первую силу 50 Н назад.
Законы Ньютона позволяют описывать и объяснять разнообразные ситуации, связанные с движением тел. Они являются основой для дальнейших исследований и применения физических принципов в реальных условиях.
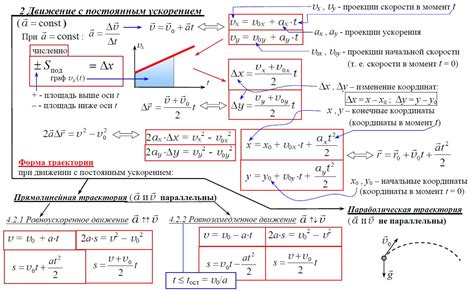
Движение с постоянным ускорением: формулы и приложения
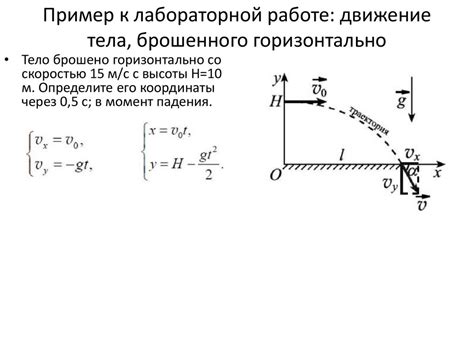
Для описания движения с постоянным ускорением существует несколько формул. Одна из них позволяет вычислить перемещение тела в зависимости от начальной скорости, ускорения и времени. Формула записывается следующим образом:
S = V₀t + (a * t²) / 2
где S - перемещение тела, V₀ - начальная скорость, t - время, a - ускорение.
Для расчета конечной скорости тела можно использовать следующую формулу:
V = V₀ + a * t
где V - конечная скорость.
Также, используя формулу для перемещения, можно выразить ускорение через начальную и конечную скорость, а также время:
a = (V - V₀) / t
Движение с постоянным ускорением широко применяется в различных областях, включая автомобильную промышленность, аэрокосмическую отрасль, строительство и прочие. Например, при расчете тормозного пути автомобиля необходимо учитывать постоянное ускорение, чтобы предсказать, какой путь он пройдет до полной остановки. Это также важно для проектирования и разработки ракет, самолетов и других транспортных средств, где движение с постоянным ускорением играет ключевую роль.
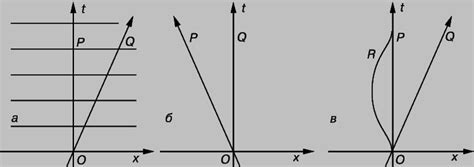
Траектория движения: понятие и виды траекторий

Прямая траектория движения характеризуется тем, что все положения объекта находятся на одной линии. Например, свободно падающее тело движется вдоль прямой вертикальной траектории.
Криволинейная траектория представляет собой изгибающуюся линию. Она может быть плавно изогнутой или иметь сложные петли и витки. Криволинейное движение часто наблюдается у объектов, движущихся под действием силы трения или воздушного сопротивления.
Замкнутая траектория характеризуется тем, что объект возвращается в исходное положение после полного оборота. Примером замкнутой траектории может служить движение планеты вокруг своей орбиты.
Периодическая траектория перемещения повторяет одинаковые фазы во времени. На протяжении определенного временного интервала объект проходит одну и ту же последовательность положений. Такая траектория часто наблюдается у колеблющихся систем и движущихся по кругу объектов.
Понимание понятия траектории и осознание различных видов траекторий позволяет углубить знания о перемещении объектов и применить соответствующие формулы и принципы физики для анализа и описания их движения.
Проектирование пути перемещения: задачи и решения

Задача проектирования пути перемещения включает в себя определение требуемых параметров, выбор подходящих материалов и конструкций, а также учет физических законов, которые определяют движение объекта.
Для решения задачи проектирования пути перемещения необходимо учитывать такие факторы, как требуемая скорость движения, нагрузка, инерционные и силовые характеристики, а также среда, в которой будет осуществляться перемещение.
Выбор подходящих материалов и конструкций является одним из важных аспектов проектирования. Материал и конструкция должны обеспечивать достаточную прочность и износостойкость, чтобы выдерживать требуемую нагрузку и частоту использования. Также важно учитывать другие свойства материала, такие как трение, амортизацию, шум и вибрацию.
Другой важный аспект - это учет физических законов, которые определяют перемещение объекта. Законы Ньютона обеспечивают понимание принципов движения и помогают определить силы, действующие на объект. Законы сохранения энергии и импульса могут использоваться для определения энергетических характеристик и стабильности движения.
Для решения задачи проектирования пути перемещения может использоваться метод конечных элементов, который позволяет провести численный анализ статических и динамических характеристик конструкции и предсказать ее поведение в различных условиях.
Также можно использовать моделирование и симуляцию для проверки предлагаемого пути перемещения и определения его эффективности. Это позволяет исследовать различные варианты и выбрать наилучшее решение.
В конечном итоге, проектирование пути перемещения требует тщательного анализа и интеграции различных факторов. Это позволяет создать оптимальную систему, которая обеспечивает безопасное и эффективное перемещение объектов.