В геометрии, вписанная окружность треугольника является особенной фигурой, которая проходит через вершины треугольника и касается всех его сторон. Радиус этой окружности является важным параметром треугольника и может быть использован для решения различных задач в геометрии и физике.
Определение радиуса вписанной окружности треугольника является весьма нетривиальной задачей, и, до недавнего времени, требовало сложных и долгих вычислений. Теперь же благодаря развитию математических методов, существуют более простые и эффективные способы для расчета данного параметра.
Формула для нахождения радиуса вписанной окружности треугольника основана на свойствах перпендикуляра, проведенного из центра окружности к одной из сторон треугольника. Для получения этого значения необходимо знать лишь длины сторон треугольника и его полупериметр.
Как найти радиус вписанной окружности треугольника?
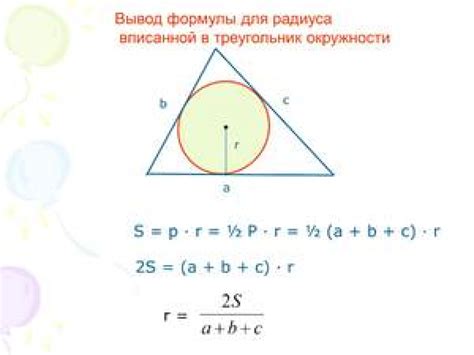
Одна из наиболее эффективных формул для нахождения радиуса вписанной окружности треугольника основана на длинах сторон треугольника. Для применения этой формулы необходимо знать длины всех сторон треугольника. Формула выглядит следующим образом:
r = (a + b + c) / (2 * p)
Где:
r - радиус вписанной окружности
a, b, c - длины сторон треугольника
p - полупериметр треугольника (p = (a + b + c) / 2)
Чтобы найти радиус вписанной окружности треугольника, нужно сначала найти длины всех его сторон, затем вычислить полупериметр треугольника и наконец применить формулу, указанную выше. Результатом будет радиус, который позволит построить вписанную окружность треугольника.
Определение вписанной окружности треугольника
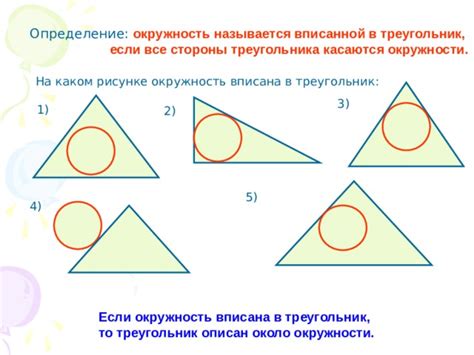
Для определения вписанной окружности треугольника необходимо знать длины его сторон и углы. Существуют различные способы вычисления радиуса вписанной окружности, некоторые из них более эффективны и точные, чем другие.
Одним из эффективных способов вычисления радиуса вписанной окружности треугольника является использование формулы радиуса вписанной окружности:
r = (S / p)
где r - радиус вписанной окружности, S - площадь треугольника, p - полупериметр треугольника (сумма длин всех его сторон, разделенная на 2).
Эта формула позволяет быстро и точно вычислить радиус вписанной окружности треугольника. Для этого необходимо найти площадь треугольника, используя, например, формулу Герона, затем вычислить полупериметр и, наконец, подставить значения в формулу радиуса вписанной окружности.
Зная радиус вписанной окружности треугольника, можно решать задачи, связанные с нахождением других параметров треугольника, таких как высоты, длины сторон и углов. Также радиус вписанной окружности имеет множество применений в геометрии, физике и других науках.
Формула для расчета радиуса вписанной окружности
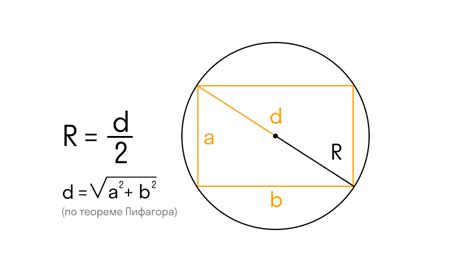
Для того чтобы найти радиус вписанной окружности треугольника, существует простая и эффективная формула, основанная на известных свойствах треугольника и его вписанной окружности.
Формула выглядит следующим образом:
| r = | площадь треугольника | / | полупериметр треугольника |
Здесь r - радиус вписанной окружности, площадь треугольника - это площадь самого треугольника, а полупериметр - половина суммы длин всех его сторон.
Используя эту формулу, вы сможете легко и точно определить радиус вписанной окружности в любом треугольнике. Зная радиус вписанной окружности, вы сможете решать различные задачи, связанные с треугольниками и окружностями.
Шаги для эффективного расчета

- Измерьте длины всех сторон треугольника. Обозначьте эти длины как a, b и c.
- Найдите полупериметр треугольника, вычислив сумму всех сторон, поделив ее на 2: p = (a + b + c) / 2.
- Используйте формулу для вычисления радиуса вписанной окружности треугольника: r = √((p - a)(p - b)(p - c) / p), где p - полупериметр треугольника.
Теперь, зная длины сторон треугольника и радиус вписанной окружности, вы можете использовать эти значения для решения различных задач геометрии, таких как нахождение площади треугольника или координат вершин треугольника.
Примеры расчетов

Для наглядности, рассмотрим несколько примеров расчета радиуса вписанной окружности треугольника.
Пример 1:
Известны стороны треугольника: a = 5 см, b = 8 см, c = 7 см.
Для начала, найдем полупериметр треугольника по формуле:
p = (a + b + c) / 2 = (5 + 8 + 7) / 2 = 10 см.
Затем, используем формулу для радиуса вписанной окружности:
r = √((p-a)(p-b)(p-c) / p) = √((10-5)(10-8)(10-7) / 10) = √(5*2*3 / 10) = 1.73 см.
Таким образом, радиус вписанной окружности треугольника составляет 1.73 см.
Пример 2:
Известны стороны треугольника: a = 12 м, b = 9 м, c = 15 м.
Найдем полупериметр треугольника:
p = (a + b + c) / 2 = (12 + 9 + 15) / 2 = 18 м.
Применим формулу для нахождения радиуса вписанной окружности:
r = √((p-a)(p-b)(p-c) / p) = √((18-12)(18-9)(18-15) / 18) = √(6*9*3 / 18) = √6 м.
Следовательно, радиус вписанной окружности для данного треугольника равен √6 м.
Пример 3:
Известны стороны треугольника: a = 7.5 см, b = 7.5 см, c = 7.5 см.
Найдем полупериметр треугольника:
p = (a + b + c) / 2 = (7.5 + 7.5 + 7.5) / 2 = 11.25 см.
Применим формулу для нахождения радиуса вписанной окружности:
r = √((p-a)(p-b)(p-c) / p) = √((11.25-7.5)(11.25-7.5)(11.25-7.5) / 11.25) = √(3.75*3.75*3.75 / 11.25) ≈ 3.08 см.
Таким образом, радиус вписанной окружности для данного треугольника приближенно равен 3.08 см.
Приложение для автоматического расчета

Для удобства и эффективности расчета радиуса вписанной окружности треугольника, существует специальное приложение, которое позволяет выполнить эту операцию автоматически. Приложение основано на использовании формулы, которая определена для такого расчета.
Для увеличения удобства использования, приложение может быть доступно на мобильных устройствах, что позволяет проводить расчеты в любое время и в любом месте. Кроме того, оно может быть интегрировано с другими программами или использоваться в качестве модуля в больших проектах.
Такое приложение значительно упрощает процесс расчета радиуса вписанной окружности треугольника и позволяет сэкономить время и усилия. Благодаря ему можно точно и быстро получить необходимый результат. Поэтому использование такого приложения является оптимальным решением для всех, кто занимается геометрией или связанными с ней расчетами.
| Преимущества приложения для автоматического расчета |
|---|
| 1. Простота использования и интуитивно понятный интерфейс |
| 2. Возможность проводить расчеты в любое время и в любом месте |
| 3. Интеграция с другими программами или использование в крупных проектах |
| 4. Высокая точность и быстрота расчетов |
Практическое применение

Знание радиуса вписанной окружности треугольника имеет множество практических применений в различных областях.
Одно из основных применений заключается в геометрии. Радиус вписанной окружности является важным параметром при решении задач, связанных с треугольниками. Например, зная радиус вписанной окружности и длины сторон треугольника, можно узнать площадь треугольника по формуле S = pr, где S - площадь треугольника, p - полупериметр треугольника, а r - радиус вписанной окружности.
Также радиус вписанной окружности используется при расчете площади фигур, которые можно разбить на треугольники. Например, площадь круга можно найти, разбив его на бесконечное количество треугольников, каждый из которых имеет радиус вписанной окружности в качестве стороны.
В архитектуре и строительстве радиус вписанной окружности также играет важную роль. Он помогает определить точку пересечения биссектрис треугольника, что помогает в расстановке мебели, решении конструкционных задач и дизайне интерьера.
В медицине радиус вписанной окружности используется при изготовлении протезов и ортопедических устройств. Например, при разработке протеза для замены пораженного сустава у пациента, радиус вписанной окружности может быть использован для определения точных размеров протеза.