Существует широко распространенное заблуждение, что натуральные числа могут иметь только положительные значения. Однако, глубже изучая математику, мы можем обнаружить, что это представление не является единственно возможным. Возникает вопрос: а на сколько далека от истины эта распространенная позиция?
Один из аргументов в пользу существования натуральных чисел с отрицательными значениями связан с понятием противоположного числа. К примеру, если у нас есть число 5, то мы можем найти его противоположное значение, равное -5. Это означает, что оба числа, и положительное, и отрицательное, лежат на одной числовой прямой, и между ними нет каких-либо различий в понимании.
Еще одним аргументом в пользу существования натуральных чисел с отрицательными значениями является математическая операция вычитания. Если мы вычитаем одно число из другого, и первое число меньше второго, то результат будет отрицательным числом. Это подтверждает тот факт, что отрицательные числа имеют реальный математический смысл и являются неотъемлемой частью числовой системы.
Распространенные заблуждения о натуральных числах с отрицательными значениями
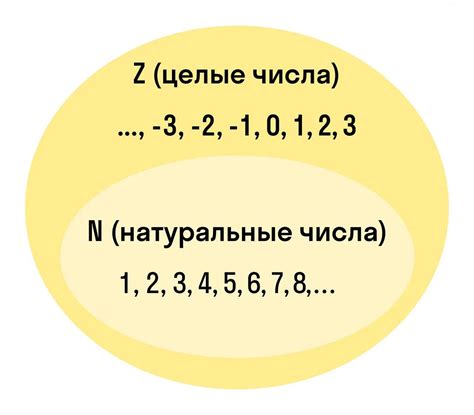
Миф: Натуральные числа не могут иметь отрицательные значения.
Реальность: Натуральные числа определяются как положительные целые числа, начиная с единицы и продолжая до бесконечности. Они использовались людьми с древнейших времен для счета и измерения. Однако, в математическом смысле, натуральные числа не включают отрицательные значения.
Миф: Натуральные числа с отрицательными значениями существуют в компьютерных программировании.
Реальность: В компьютерных программировании обычно используется различные типы целых чисел, такие как целые числа (integers), знаковые целые числа (signed integers), беззнаковые целые числа (unsigned integers) и другие. Но все они определяются в соответствии с математическими определениями, и натуральные числа не включают отрицательные значения.
Миф: Отрицательные значения некоторых величин могут быть интерпретированы как натуральные числа.
Реальность: Натуральные числа представляют собой абстрактное понятие, которое не может быть применено к отрицательным значениям. Однако, в некоторых случаях, отрицательные значения могут быть использованы для обозначения дополнительных свойств или состояний величин, но это не является интерпретацией их как натуральных чисел.
Миф о самом понятии натуральных чисел

Понятие натуральных чисел возникло из необходимости счета и упорядочивания объектов. Начиная с единицы, мы можем посчитать все целые положительные числа. Однако, в реальной жизни часто возникает необходимость в учете и обозначении долгов, убытков или отрицательных значений каких-либо величин.
Таким образом, для того чтобы учесть отрицательные значения, было введено понятие целых чисел, которые включают в себя как положительные, так и отрицательные числа. При этом натуральные числа как подмножество целых чисел остаются положительными, начиная с единицы.
Таким образом, миф о том, что натуральные числа не могут быть отрицательными, не соответствует действительности. Натуральные числа включают только положительные значения, в то время как целые числа охватывают как положительные, так и отрицательные значения.
Реально существующие отрицательные натуральные числа
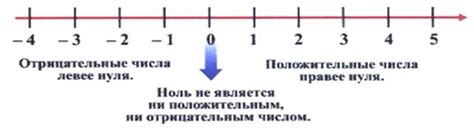
Понятие "отрицательного натурального числа" кажется противоречием в себе. Ведь "натуральные числа" определяются как положительные числа, используемые для подсчета элементов в наборе.
Однако, в математике существует концепция целых чисел, которая включает и отрицательные числа. Целые числа обозначаются символом Z и представляются в виде числовой оси, где ноль является точкой, разделяющей положительные и отрицательные числа.
Таким образом, отрицательные числа также входят в понятие "целых чисел", и, следовательно, можно говорить о существовании отрицательных натуральных чисел.
Отрицательные натуральные числа могут быть полезны в различных математических анализах и моделях. Они позволяют учитывать долги, убытки, температуру, направление движения и другие явления, которые могут быть представлены отрицательными значениями в реальном мире.
Несмотря на то, что понятие отрицательных натуральных чисел может вызывать некоторые сомнения, они являются важной математической концепцией и имеют свои применения в реальном мире.
Примеры использования отрицательных натуральных чисел в математике

Отрицательные натуральные числа могут быть абстрактными понятиями, но они находят широкое применение в различных областях математики.
Алгебра: Отрицательные натуральные числа используются при работе с алгебраическими операциями, такими как сложение и вычитание. Они позволяют описывать убывающие последовательности, задавать отрицательные значения в уравнениях и неравенствах, а также работать с комплексными числами.
Геометрия: Отрицательные натуральные числа используются для обозначения координат в декартовой системе координат. Они помогают задавать точки в пространстве с отрицательными координатами и определять расстояния и направления между ними.
Теория чисел: Отрицательные натуральные числа встречаются при изучении делителей и кратных чисел. Они позволяют обобщить понятие простых чисел на отрицательные значения и исследовать их свойства.
Финансы: Отрицательные натуральные числа используются при моделировании финансовых потоков. Они помогают учитывать затраты, убытки и долги, а также определять прибыльность и рентабельность проектов.
Статистика: Отрицательные натуральные числа могут быть использованы для обозначения различных показателей, таких как изменение значения показателя по сравнению с предыдущим периодом или относительное отклонение от среднего значения.
Влияние отрицательных натуральных чисел на работу компьютерных систем

Вопрос о существовании отрицательных натуральных чисел долгое время был предметом споров и дебатов в области математики. Некоторые ученые считали, что отрицательные значения натуральных чисел лишь теоретическое понятие, не имеющее практического применения. Однако, с развитием компьютерных систем и программного обеспечения, мы убедились в том, что отрицательные натуральные числа действительно имеют влияние на работу этих систем.
Когда мы работаем с отрицательными натуральными числами, компьютерные системы используют специальный формат представления чисел - дополнительный код. Этот формат позволяет представить отрицательное число в виде битовой последовательности, где старший бит указывает на знак числа.
Важно отметить, что работа с отрицательными натуральными числами может быть более сложной и требовательной по вычислительным ресурсам. Некорректное использование отрицательных чисел может привести к ошибкам в программном коде, а также к неправильным результатам вычислений. Поэтому разработчикам программного обеспечения необходимо быть внимательными и аккуратными при работе с отрицательными натуральными числами.
Кроме того, использование отрицательных натуральных чисел может оказывать влияние на производительность компьютерных систем. Например, операции сложения и вычитания с отрицательными числами могут требовать больше времени и ресурсов для выполнения по сравнению с операциями с положительными числами. Использование отрицательных чисел также может затруднить работу с определенными алгоритмами и структурами данных.