Прямоугольный треугольник – это геометрическая фигура, у которой один из углов равен 90 градусам. Он состоит из двух катетов и гипотенузы. Катеты - это стороны треугольника, которые составляют угол в 90 градусов. Гипотенуза - самая длинная сторона треугольника, которая противуположна прямому углу.
Как найти катет и угол прямоугольного треугольника? Когда известны длина гипотенузы и одного из катетов, можно найти длину второго катета с помощью Пифагоровой теоремы. По теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы.
Для нахождения угла прямоугольного треугольника можно использовать тригонометрические функции. Например, если известна длина катета и гипотенузы, можно найти синус или косинус угла. Если известны длины двух катетов, можно найти тангенс угла. С помощью таблицы тригонометрических функций можно найти значения углов для данных длин сторон треугольника.
Метод синусов и косинусов

Существует несколько методов для нахождения катетов и углов в прямоугольном треугольнике. Один из таких методов называется методом синусов и косинусов.
Метод синусов основан на соотношении между длинами сторон и синусами углов треугольника. Для любого треугольника ABC с прямым углом C дана формула:
$$\sin C = \frac{BC}{AB}$$
где BC - катет треугольника, AB - гипотенуза треугольника, C - угол противоположный катету BC.
Для нахождения катета треугольника можно использовать формулу:
$$BC = \sin C \cdot AB$$
Метод косинусов основан на соотношении между длинами сторон и косинусами углов треугольника. Для любого треугольника ABC с прямым углом C дана формула:
$$\cos C = \frac{AC}{AB}$$
где AC - катет треугольника, AB - гипотенуза треугольника, C - угол противоположный катету AC.
Для нахождения катета треугольника можно использовать формулу:
$$AC = \cos C \cdot AB$$
Таким образом, метод синусов и косинусов позволяет находить длины катетов треугольника, исходя из известной длины гипотенузы и значения угла.
Используйте формулу Пифагора
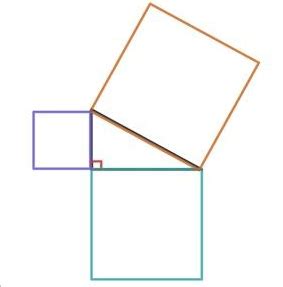
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Для использования этой формулы, необходимо знать длины двух из трех сторон прямоугольного треугольника. Другой способ использования этой формулы – нахождение угла между гипотенузой и одним из катетов.
Ниже приведена таблица, которая демонстрирует примеры использования формулы Пифагора для нахождения катета и угла прямоугольного треугольника.
| Дано | Искомое | Формула |
|---|---|---|
| Гипотенуза и один катет | Другой катет | Катет = √(Гипотенуза² - Известный катет²) |
| Два катета | Гипотенуза | Гипотенуза = √(Катет₁² + Катет₂²) |
| Гипотенуза и один катет | Угол между гипотенузой и известным катетом | Угол = arcsin(Известный катет / Гипотенуза) |
Формула Пифагора является универсальным инструментом для решения задач на нахождение катетов и углов прямоугольного треугольника. Она может быть применена в различных сферах, таких как физика, архитектура, геометрия и других.
Примените теорему косинусов
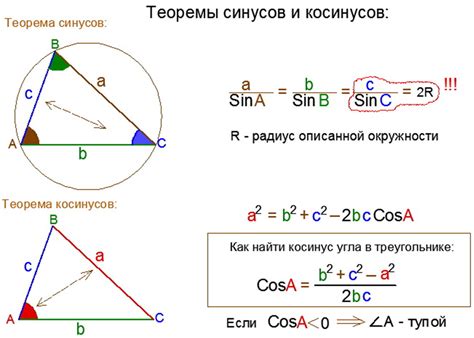
Формула теоремы косинусов выглядит следующим образом:
c^2 = a^2 + b^2 - 2ab * cos(C)
где c - гипотенуза треугольника, a и b - катеты, C - угол между гипотенузой и одним из катетов.
Чтобы найти катет треугольника, можно переставить формулу теоремы косинусов и решить ее относительно нужного катета. Например, чтобы найти катет a:
a = sqrt(c^2 - b^2 + 2ab * cos(C))
А чтобы найти угол C, можно использовать обратную функцию косинуса:
C = arccos((a^2 + b^2 - c^2) / 2ab)
Применение теоремы косинусов позволяет точно вычислить значения катета и угла прямоугольного треугольника и применить их в решении задач и конструкциях.
Определите катет с помощью тангенса
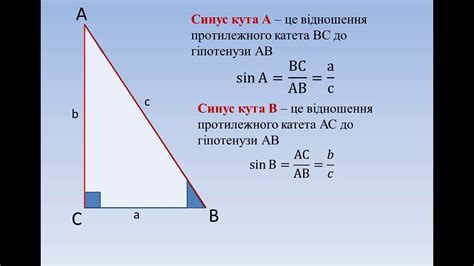
Тангенс угла определяется как отношение противолежащего катета к прилежащему катету. Таким образом, чтобы найти катет, необходимо знать значение тангенса угла и длину другого катета.
Для определения катета с помощью тангенса необходимо выполнить следующие шаги:
- Найдите значение тангенса угла, используя соотношение тангенса: тангенс угла равен противолежащему катету, деленному на прилежащий катет.
- Умножьте значение тангенса на длину известного катета, чтобы определить длину неизвестного катета.
Например, если известна длина противолежащего катета и значение тангенса угла, можно найти длину прилежащего катета. Для этого необходимо разделить длину противолежащего катета на значение тангенса угла.
Использование тангенса угла позволяет с легкостью определить длину катета в прямоугольном треугольнике.
Найдите угол с помощью арктангенса

Для нахождения угла прямоугольного треугольника с помощью арктангенса необходимо знать значения катетов.
1. Зная значения катетов a и b прямоугольного треугольника, можно использовать формулу:
- Вычислите отношение длины катета a к длине катета b: a/b.
- Используя арктангенс функцию научного калькулятора или математическую функцию в программном коде, найдите обратное значение отношения.
- Умножьте результат на 180 и разделите на π (пи), чтобы получить значение угла в градусах.
2. Обратный процесс:
- Зная длину катета a и значение угла α, используйте тангенс функцию для вычисления значения катета b: b = a/tan(α).
Эти методы широко используются в математике и физике при работе с прямоугольными треугольниками.
Пользуйтесь теоремой синусов
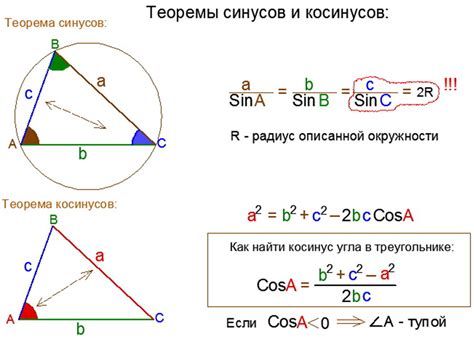
Формула теоремы синусов выглядит следующим образом:
a / sin(A) = b / sin(B) = c / sin(C)
Где:
- a - длина стороны противолежащей углу А
- b - длина стороны противолежащей углу В
- c - длина гипотенузы
- A - угол, противолежащий стороне a
- B - угол, противолежащий стороне b
- C - угол, противолежащий стороне c
Для применения теоремы синусов достаточно знать длины двух сторон и значение угла между ними.
Пример использования теоремы синусов:
- Известно, что длина стороны a равна 5 и длина стороны b равна 7.
- Также известно, что угол между этими сторонами, C, равен 60 градусов.
- Применяя формулу теоремы синусов, можно найти длину гипотенузы c.
- Для этого подставим известные значения в формулу: 5 / sin(60) = c / sin(C).
- Решая данное уравнение, найдем c: c = 7.07.
Таким образом, используя теорему синусов, можно находить катеты и углы прямоугольного треугольника без необходимости в сложных вычислениях и таблицах.
Решите прямоугольный треугольник с помощью Герона

Для использования Героновой формулы, необходимо знать длины катетов треугольника. Обозначим их как a и b. Тогда длина гипотенузы будет равна:
c = √(a^2 + b^2)
Для нахождения углов прямоугольного треугольника используется тригонометрическая функция тангенс. Угол α можно вычислить по формуле:
α = atan(a / b)
А угол β будет:
β = 90° - α
Где atan - обратная тангенс функция.
Теперь вы можете использовать Геронову формулу, чтобы решить прямоугольный треугольник и найти длину гипотенузы и углы треугольника.