Арксинус и арккосинус - это обратные функции для синуса и косинуса соответственно. Они позволяют нам находить углы, значение синуса или косинуса которых равно заданному числу. В данной статье мы рассмотрим нахождение этих углов на единичной окружности.
Единичная окружность - это окружность с радиусом, равным единице. Она играет важную роль в тригонометрии, так как позволяет устанавливать связь между углами и значениями тригонометрических функций. Каждая точка на единичной окружности соответствует определенному углу, который мы можем выразить с помощью арксинуса или арккосинуса.
Для нахождения арксинуса или арккосинуса нужно найти точку на окружности, от которой провести вертикальную или горизонтальную линию, пересекающую ось ординат или абсцисс. Этот отрезок будет представлять значения арксинуса или арккосинуса для данного угла. Таким образом, арксинус угла равен длине отрезка, проведенного от точки на окружности до оси ординат, а арккосинус - отрезка от точки на окружности до оси абсцисс.
Что такое арксинус и арккосинус?

Функция арксинус возвращает угол, который имеет заданный синус, в интервале от -π/2 до π/2. Например, если sin(θ) = 0.5, то арксинус этого значения будет равен π/6, так как это угол, который имеет синус 0.5.
Функция арккосинус возвращает угол, который имеет заданный косинус, в интервале от 0 до π. Например, если cos(θ) = 0.5, то арккосинус этого значения будет равен π/3, так как это угол, который имеет косинус 0.5.
Важно отметить, что арксинус и арккосинус являются обратными функциями лишь в определенных интервалах значений. За пределами этих интервалов значения этих функций не определены.
Примечание: Для обозначения арксинуса и арккосинуса также используют обозначения asin и acos соответственно.
Арксинус и арккосинус: основные понятия
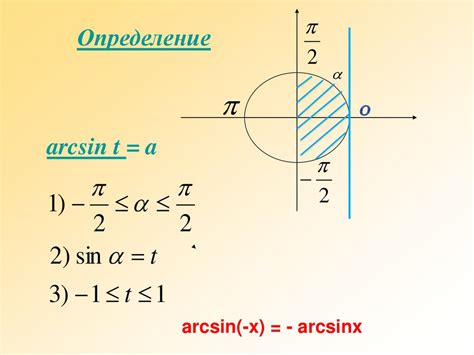
Синус (sin) и косинус (cos) - это тригонометрические функции, которые широко используются в математике и науке для описания и анализа колебательных процессов, волновых функций, гармонических колебаний и многих других явлений.
Арксинус (asin) и арккосинус (acos) - это функции, которые позволяют найти угол, значение синуса или косинуса которого равно заданному числу. Они являются обратными функциями синуса и косинуса и помогают решать уравнения и задачи, связанные с тригонометрией.
Значение арксинуса и арккосинуса всегда находится в интервале от -π/2 до π/2 радиан (или от -90° до 90°). Таким образом, возвращаемый результат является углом, выраженным в радианах или градусах.
Чтобы найти значение арксинуса или арккосинуса, можно использовать тригонометрические таблицы, калькуляторы с тригонометрическими функциями или специальные математические программы.
Примеры:
Если синус угла равен 0.5, то арксинус этого значения будет равен 30° (или π/6 радиан).
Если косинус угла равен 0.8, то арккосинус этого значения будет равен 36.87° (или 0.6435 радиан).
Арксинус и арккосинус являются важными инструментами в тригонометрии и научных исследованиях. Их использование позволяет более точно анализировать и решать задачи, связанные с углами и тригонометрическими функциями.
Тригонометрические функции на окружностях

Тригонометрические функции на окружностях широко применяются в математике, физике и других науках. Они позволяют нам вычислять значения синуса, косинуса, тангенса и других функций для заданных углов на единичной окружности.
Окружность, на которой определены тригонометрические функции, называется тригонометрической окружностью. Она имеет радиус 1 и центр в начале координат.
В тригонометрии наиболее часто используются две основные функции - синус и косинус. Синус угла определяется как отношение длины противоположного катета к гипотенузе, а косинус - как отношение длины прилежащего катета к гипотенузе.
Зная значения синуса и косинуса для заданного угла, мы можем вычислить значения других тригонометрических функций, таких как тангенс, котангенс, секанс и косеканс.
Арксинус и арккосинус - это обратные функции синуса и косинуса. Они позволяют находить значение угла по заданным значениям синуса или косинуса.
Нахождение арксинуса и арккосинуса на окружности осуществляется с использованием тригонометрических соотношений и формул. Эти формулы позволяют нам вычислить значение угла, зная значения синуса или косинуса.
Таким образом, тригонометрические функции на окружностях являются важными инструментами для решения задач, связанных с углами и тригонометрией. Они позволяют нам моделировать и анализировать различные явления, такие как колебания, волны, движение и другие.
Графическое представление арксинуса и арккосинуса

Для построения графика арксинуса используется окружность с радиусом единица, центр которой находится в начале координат. По определению, арксинус угла α - это радианная мера дуги окружности, начинающейся в точке (0,0) и заканчивающейся в точке (sin α, α). Таким образом, на графике арксинуса точка (α, arcsin α) лежит на дуге окружности с радиусом единица.
Аналогично, для графического представления арккосинуса используется окружность с радиусом единица, центр которой расположен в начале координат. Арккосинус угла α - это радианная мера дуги окружности, начинающейся в точке (0,0) и заканчивающейся в точке (α, arccos α). Точка (α, arccos α) лежит на дуге окружности с радиусом единица.
Графическое представление арксинуса и арккосинуса позволяет наглядно увидеть, как значение этих функций изменяется в зависимости от аргумента. Оно также помогает уяснить свойства и особенности арксинуса и арккосинуса, такие как периодичность и ограниченность значений.
Формулы для нахождения арксинуса и арккосинуса

Формула для вычисления арксинуса имеет вид:
| arcsin(x) = | sin-1(x) |
где x - значение синуса угла. Результатом работы формулы будет угол, значение синуса которого равно x.
Формула для вычисления арккосинуса выглядит следующим образом:
| arccos(x) = | cos-1(x) |
где x - значение косинуса угла. Результатом работы формулы будет угол, значение косинуса которого равно x.
Формулы для арксинуса и арккосинуса позволяют узнать значение угла на окружности, имея заранее известные значения синуса или косинуса. Это особенно полезно при решении геометрических и тригонометрических задач.
Примеры вычислений арксинуса и арккосинуса

Для вычисления арксинуса и арккосинуса угла на окружности, необходимо знать значение синуса или косинуса этого угла. Возьмем несколько примеров вычислений арксинуса и арккосинуса:
- Вычислим арксинус угла, для которого синус равен 1/2. Зная, что синус π/6 равен 1/2, получаем, что арксинус 1/2 равен π/6.
- Найдем арккосинус угла, для которого косинус равен -1/2. Зная, что косинус 7π/6 равен -1/2, получаем, что арккосинус -1/2 равен 7π/6.
- Рассчитаем арксинус угла, для которого синус равен 0. Зная, что синус π равен 0, получаем, что арксинус 0 равен π.
- Построим график арксинуса функции y = sin(x) на интервале [-π/2, π/2]. Из графика видно, что арксинус принимает значения от -π/2 до π/2, соответствующие углам от -90° до 90°.
- Изобразим график арккосинуса функции y = cos(x) на интервале [0, π]. График арккосинуса принимает значения от 0 до π, что соответствует углам от 0° до 180°.
Таким образом, вычисление арксинуса и арккосинуса угла на окружности позволяет определить значение этого угла в радианах и градусах, а также представить его на графике. Это важные математические операции, которые находят применение в различных областях науки и техники.
Свойства арксинуса и арккосинуса

Свойства арксинуса:
- Значение арксинуса лежит в интервале от -π/2 до π/2.
- Арксинус отрицательного числа равен отрицательному арксинусу положительного числа с тем же модулем: asin(-x) = -asin(x).
- Арксинус нуля равен нулю: asin(0) = 0.
- Арксинус числа, превышающего 1 по модулю, не имеет действительных значений.
Свойства арккосинуса:
- Значение арккосинуса лежит в интервале от 0 до π.
- Арккосинус отрицательного числа равен π минус арккосинус положительного числа с тем же модулем: acos(-x) = π - acos(x).
- Арккосинус 1 равен нулю: acos(1) = 0.
- Арккосинус числа, превышающего 1 по модулю, не имеет действительных значений.
Знание свойств арксинуса и арккосинуса необходимо для решения различных задач, связанных с геометрией и тригонометрией, а также для работы с комплексными числами и рядом других математических областей.
Применение арксинуса и арккосинуса в математике

Арксинус используется для нахождения значения угла, при котором синус этого угла равен заданному числу. Это позволяет решать уравнения вида sin(x) = a, где a – известное число. Арксинус также используется при вычислении площадей и объёмов фигур, связанных с синусоидальными функциями.
Например, если нам известно, что sin(x) = 0.5, то можем использовать арксинус для нахождения значения угла x. Арксинус от 0.5 равен 30 градусам (или π/6 радиан). Таким образом, x = 30 градусам (или π/6 радиан).
Арккосинус позволяет найти значение угла, при котором косинус этого угла равен заданному числу. Это полезно при решении уравнений типа cos(x) = a, где a – известное число. Арккосинус также применяется при анализе геометрических фигур, таких как окружности и треугольники.
Например, если нам нужно найти угол x, при котором cos(x) = 0.8, то мы можем использовать арккосинус. Арккосинус от 0.8 равен ≈ 36.87 градусам (или ≈ 0.6435 радиана). Таким образом, x ≈ 36.87 градуса (или ≈ 0.6435 радиана).
Арксинус и арккосинус являются важными инструментами для решения задач, связанных с тригонометрией и геометрией. Они позволяют находить значения углов, которые соответствуют заданным значениям синуса и косинуса.