Решение задач, связанных с треугольниками, является ключевым навыком в математике. Одной из таких задач является нахождение катетов через гипотенузу и угол. Этот метод решения задач представляет собой надежный и простой способ, позволяющий вычислить значения катетов треугольника.
Во многих задачах, требующих нахождения длин катетов, даны значения гипотенузы и угла. Для решения таких задач можно использовать тригонометрию. Она позволяет связать стороны треугольника с его углами, что делает возможным вычисление значений катетов по известным данным.
Для нахождения катетов через гипотенузу и угол можно использовать тригонометрические функции. Например, если известна гипотенуза c и угол α между гипотенузой и одним из катетов, то значение одного из катетов a можно найти с помощью тригонометрической функции синус: a = c * sin(α).
Метод нахождения катетов через гипотенузу
Найдем способ нахождения катетов прямоугольного треугольника, если известна его гипотенуза и один из углов.
Пусть дан прямоугольный треугольник ABC, в котором гипотенуза AB известна, а угол A также известен. Найдем катеты AC и BC.
Для начала, вспомним соотношения в прямоугольном треугольнике:
- синус угла равен отношению противолежащего катета к гипотенузе: sin(A) = AC / AB;
- косинус угла равен отношению прилежащего катета к гипотенузе: cos(A) = BC / AB.
Используя эти соотношения, мы можем выразить катеты через гипотенузу и угол:
- катет AC можно найти, умножив гипотенузу AB на синус угла A: AC = AB * sin(A);
- катет BC можно найти, умножив гипотенузу AB на косинус угла A: BC = AB * cos(A).
Таким образом, зная гипотенузу и один из углов, мы можем легко найти катеты прямоугольного треугольника. Этот метод очень полезен при решении различных задач в математике, физике и других науках.
Пример:
Пусть у нас есть прямоугольный треугольник ABC, где гипотенуза AB = 10 см, а угол A = 30 градусов. Найдем катеты AC и BC:
AC = AB * sin(A) = 10 * sin(30) = 5 см
BC = AB * cos(A) = 10 * cos(30) = 8.66 см
Таким образом, катет AC равен 5 см, а катет BC равен 8.66 см.
Используя данный метод, вы сможете легко находить катеты прямоугольного треугольника, если известны гипотенуза и угол. Это простой и эффективный способ решения задач в математике.
Определение катетов через гипотенузу и угол
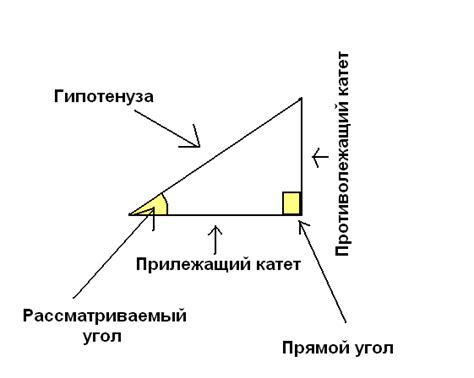
Для определения катетов, нам необходимо знать значение гипотенузы и значение одного из углов прямоугольного треугольника. Если известны гипотенуза и угол, то мы можем легко найти значение катетов.
Допустим, у нас есть прямоугольный треугольник, в котором известны гипотенуза и один из углов, например, угол α. Чтобы найти значение катетов, мы можем воспользоваться тригонометрическими функциями.
Для нахождения катета, прилегающего к углу α, мы можем использовать функцию синус. Значение этого катета можно найти, умножив синус угла α на значение гипотенузы.
Для нахождения катета, противоположного углу α, мы можем использовать функцию косинус. Значение этого катета можно найти, умножив косинус угла α на значение гипотенузы.
Также, можно воспользоваться функцией тангенс для нахождения любого из катетов, зная гипотенузу и угол. Значение катета равно тангенсу угла α, умноженному на значение гипотенузы.
Воспользуемся этим методом решения задач в математике, чтобы определить значения катетов в прямоугольных треугольниках и сделать нашу работу более удобной и эффективной.
Использование теоремы Пифагора для нахождения катетов

Для нахождения катетов просто зная гипотенузу и угол, нужно использовать тригонометрические функции. В основном, используется синус и косинус определенного угла.
Допустим, у нас есть прямоугольный треугольник с гипотенузой равной h и углом α (где α - меньший из двух углов, заключенных между гипотенузой и одним из катетов). Задача - найти катеты данного треугольника.
Сначала, используя синус угла α, находим длину катета, примыкающего к углу α. Для этого вычисляем:
- Синус угла α - sin(α) = h / c, где c - гипотенуза
- Катет a = c * sin(α)
Аналогично, используя косинус угла α, можно найти длину катета, противоположного углу α. Для этого вычисляем:
- Косинус угла α - cos(α) = b / c, где b - второй катет
- Катет b = c * cos(α)
Таким образом, с помощью теоремы Пифагора и тригонометрических функций мы можем легко находить катеты прямоугольного треугольника, зная только гипотенузу и угол между гипотенузой и одним из катетов.
Расчет катетов при известной гипотенузе и угле

Для начала необходимо определить известные значения: длину гипотенузы треугольника и величину известного угла, противоположного одному из катетов. Обозначим гипотенузу как c и угол как α.
Используя тригонометрическую функцию синуса, можно выразить отношение синуса угла катету:
sin(α) = a/c
где a - длина катета треугольника.
Отсюда можно выразить длину катета a:
a = sin(α) * c
Таким образом, для нахождения длины катета необходимо умножить синус угла на длину гипотенузы.
Аналогичным образом можно найти длину второго катета, противоположного другому углу треугольника:
b = sin(β) * c
где β - величина другого известного угла, противоположного второму катету.
Таким образом, рассчитывая синусы известных углов и умножая их на длину гипотенузы, можно найти длины обоих катетов треугольника.
Применение этого метода позволяет быстро и просто находить катеты треугольника при известной гипотенузе и угле, что может быть полезно при решении различных задач в математике и геометрии.
Примеры решения задач

Пример 1:
Дана прямоугольная треугольник со сторонами a = 3, b = 4 и гипотенузой c. Найти значение гипотенузы и угла α между гипотенузой и катетом a.
Решение:
Используем формулу Пифагора: c = √(a² + b²).
Подставляем значения из условия: c = √(3² + 4²) = √(9 + 16) = √25 = 5.
Теперь найдем значение угла α с помощью тангенса: α = arctan(b/a).
Подставляем значения из условия: α = arctan(4/3) ≈ 53.13°.
Пример 2:
Дан равнобедренный прямоугольный треугольник со стороной a = 5 и гипотенузой c. Найти значение гипотенузы и угла α между гипотенузой и катетом a.
Решение:
Используем свойство равнобедренного треугольника: a = c/√2.
Подставляем значение a и находим c: 5 = c/√2, c = 5√2.
Теперь найдем значение угла α с помощью тангенса: α = arctan(a/c).
Подставляем значения из условия: α = arctan(5/(5√2)) ≈ 45°.
Пример 3:
Дан прямоугольный треугольник со сторонами a = 6, b = 8 и гипотенузой c. Найти значение гипотенузы и угла α между гипотенузой и катетом a.
Решение:
Используем формулу Пифагора: c = √(a² + b²).
Подставляем значения из условия: c = √(6² + 8²) = √(36 + 64) = √100 = 10.
Теперь найдем значение угла α с помощью синуса: α = arcsin(a/c).
Подставляем значения из условия: α = arcsin(6/10) ≈ 36.87°.
Пример 1: Нахождение длины катета при известной гипотенузе и угле
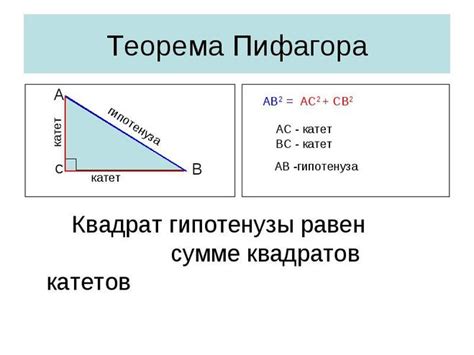
В этом примере рассмотрим задачу на нахождение длины катета прямоугольного треугольника, если известна длина гипотенузы и значение одного из углов.
Дано: гипотенуза (с) = 5 см, угол (α) = 30°.
Нам известны два из трех параметров треугольника: гипотенуза и угол. Известные значения обозначим символами: с и α.
Для начала, рассмотрим, как связаны катеты и гипотенуза в прямоугольном треугольнике по теореме Пифагора:
c = √(a² + b²),
где с - гипотенуза; а и б - катеты.
Нам известна гипотенуза (с) и значение угла (α). Найдем первый катет (а).
Так как известна длина гипотенузы и значение угла, можно воспользоваться тригонометрическими функциями, чтобы найти длину первого катета. В данном случае, будем использовать синус угла:
sin α = a / c.
Перенесем a в левую часть:
a = sin α * c.
Подставляем известные значения:
a = sin 30° * 5 см.
sin 30° равен 0.5, поэтому:
a = 0.5 * 5 см.
a = 2.5 см.
Таким образом, при известной длине гипотенузы (5 см) и заданном угле (30°), первый катет прямоугольного треугольника равен 2.5 см.
Пример 2: Расчет катетов через гипотенузу и угол в прямоугольном треугольнике
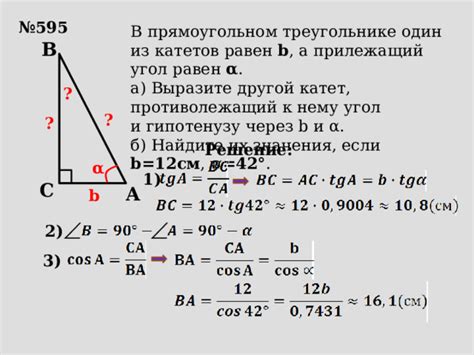
Рассмотрим следующий пример: в прямоугольном треугольнике ABC известны гипотенуза AC, равная 10 см, и угол BAC, равный 30 градусов. Необходимо найти длины катетов AB и BC.
Для решения этой задачи можно использовать тригонометрические функции. Угол BAC равен 30 градусам, а значит угол ABC равен 90 - 30 = 60 градусов. Таким образом, треугольник ABC является 30-60-90 треугольником.
В 30-60-90 треугольнике отношение длины гипотенузы к длине катета, противолежащего углу 30 градусов, равно sqrt(3):1:2. Зная длину гипотенузы AC, можем вычислить длину катета AB следующим образом:
| Отношение | Значение |
|---|---|
| Гипотенуза AC | 10 см |
| Катет AB | 10 см / sqrt(3) |
| Катет BC | 2 * 10 см / sqrt(3) |
Таким образом, получаем, что катет AB равен примерно 5.77 см, а катет BC равен примерно 11.55 см.
Применение данного метода позволяет быстро и легко находить длины катетов прямоугольного треугольника, используя только известную гипотенузу и угол. Этот метод особенно полезен при решении задач на практике, например, при расчете размеров строительных конструкций или настройке угловых измерительных приборов.
Применение метода в реальной жизни
Один из самых распространенных примеров использования этого метода - строительство. При проектировании зданий и сооружений необходимо учитывать углы и размеры треугольников. С помощью данного метода инженеры могут легко определить длину катета, если известны гипотенуза и угол. Это позволяет точно рассчитать размеры и углы различных элементов здания, таких как стены, потолки, полы и т.д., что обеспечивает их правильную установку и соответствие проекту.
Еще одним интересным примером применения данного метода является навигация. На море или в воздухе, при помощи углов и гипотенузы, можно определить точное положение объекта относительно других объектов или точек зрения. Это особенно важно при работе с компасом, картами и навигационными приборами. Зная угол и расстояние до объекта, можно точно определить его координаты и перемещаться в нужном направлении.
Метод нахождения катетов через гипотенузу и угол также применяется в автомобильной промышленности. При разработке и производстве автомобилей, инженеры используют этот метод для определения размеров и углов элементов подвески, колес, кузова и других частей. Это помогает обеспечить баланс, устойчивость и безопасность автомобиля, а также улучшить его маневренность и комфортность.
Таким образом, метод нахождения катетов через гипотенузу и угол является полезным инструментом в различных областях нашей жизни. Он помогает нам решать задачи, связанные с треугольниками и прямыми углами, и значительно упрощает процессы проектирования, навигации и производства.