В пятом классе математики, дети начинают изучать геометрию и научаются решать различные задачи, связанные с окружностями. Одной из ключевых величин, которую нужно знать при работе с окружностями, является радиус.
Радиус окружности - это расстояние от центра окружности до любой точки на ее границе. Важно понимать, что все точки на окружности находятся на одинаковом расстоянии от ее центра. Радиус обозначается буквой r и является основным параметром окружности.
Формула для нахождения радиуса окружности связана с ее диаметром. Диаметр - это отрезок, соединяющий две противоположные точки на границе окружности и проходящий через ее центр. Диаметр обозначается буквой d.
Одно из основных соотношений между радиусом и диаметром окружности выглядит так: радиус равен половине диаметра. То есть, если известен диаметр окружности, то радиус можно найти, разделив его на 2. Формула для нахождения радиуса окружности выглядит следующим образом: r = d/2.
Как найти радиус окружности в 5 классе математики: формула и примеры задач
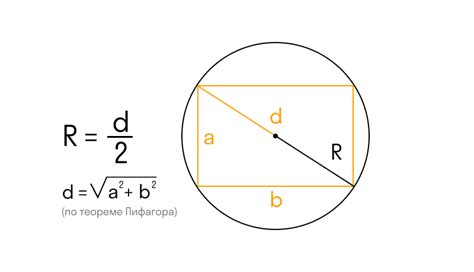
Формула для вычисления радиуса окружности выглядит следующим образом:
р = д / 2
Где "р" представляет собой радиус, а "д" - диаметр окружности.
Давайте рассмотрим несколько примеров задач, чтобы лучше понять, как применять эту формулу на практике.
- Пример 1: У нас есть окружность с диаметром 10 см. Каков радиус этой окружности?
- Пример 2: Если радиус окружности равен 8 мм. Каков будет диаметр этой окружности?
Для решения этой задачи, мы будем использовать формулу "р = д / 2". В данном случае, диаметр равен 10 см, поэтому:
р = 10 / 2 = 5 см
Таким образом, радиус этой окружности равен 5 см.
Для решения этой задачи, мы также будем использовать формулу "р = д / 2". В данном случае, радиус равен 8 мм, поэтому:
8 = д / 2
Умножим обе части на 2, чтобы избавиться от деления:
д = 8 * 2 = 16 мм
Таким образом, диаметр этой окружности равен 16 мм.
Знание формулы для вычисления радиуса окружности и применение ее в задачах позволяют легко решать задачи, связанные с окружностями. Это важный навык в математике и может быть полезным во многих практических ситуациях.
Что такое окружность и радиус?
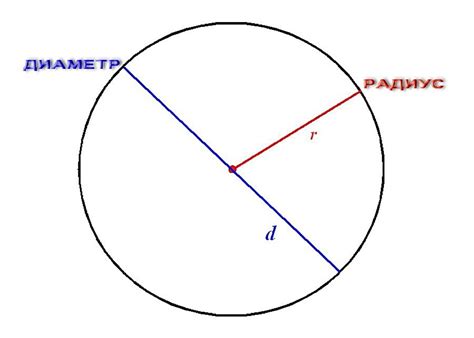
Радиус - это отрезок, соединяющий центр окружности с любой точкой на окружности. Радиус является самым коротким расстоянием от центра до точек окружности.
Таким образом, радиус определяет размер окружности и является ключевой метрической характеристикой этой фигуры. Радиус обозначается символом "r".
Формула для нахождения радиуса окружности: r = d/2, где "d" - диаметр окружности. Диаметр - это отрезок, проходящий через центр окружности и соединяющий две точки на окружности.
Для решения задач, связанных с нахождением радиуса окружности, необходимо знать длину диаметра или другие характеристики, связанные с окружностью, такие как площадь или длина окружности.
Как найти радиус окружности?
Если известен диаметр окружности, то радиус можно найти, разделив диаметр на 2. Формула для вычисления радиуса окружности выглядит следующим образом:
Радиус = Диаметр / 2
Например, если диаметр окружности равен 10 см, то радиус будет равен 5 см (10 / 2 = 5).
Если известна длина окружности, то радиус можно найти, разделив длину на 2π (число π примерно равно 3,14). Формула для вычисления радиуса окружности по длине выглядит следующим образом:
Радиус = Длина окружности / (2 * π)
Например, если длина окружности равна 20 см, то радиус будет приблизительно равен 3,18 см (20 / (2 * 3,14) ≈ 3,18).
Используя эти формулы, можно легко находить радиус окружности и решать различные задачи связанные с этой геометрической фигурой.
Примеры задач на нахождение радиуса окружности
Для нахождения радиуса окружности, помимо формулы, необходимо знать значения других характеристик этой фигуры, таких как длина диаметра или периметр. Рассмотрим несколько примеров задач, в которых нужно найти радиус окружности.
Пример 1:
Дана окружность с периметром 20 см. Найдите ее радиус.
Решение:
Периметр окружности равен сумме длин окружности и диаметра. Зная, что диаметр равен удвоенному радиусу, можно записать уравнение:
20 = 2πr + 2r
Упростим это уравнение:
20 = 2r(π + 1)
Разделим обе части уравнения на 2(π + 1):
r = 20 / (2π + 2)
Таким образом, радиус окружности равен 10 / (π + 1) см.
Пример 2:
Дана окружность с диаметром 8 м. Найдите ее радиус.
Решение:
Диаметр окружности равен удвоенному радиусу. Используем этот факт для записи уравнения:
8 = 2r
Разделим обе части уравнения на 2:
r = 4
Таким образом, радиус окружности равен 4 м.
Пример 3:
Дана окружность с длиной диаметра 14 см. Найдите ее радиус.
Решение:
Длина диаметра равна удвоенному радиусу. Запишем уравнение:
14 = 2r
Разделим обе части уравнения на 2:
r = 7
Таким образом, радиус окружности равен 7 см.
Нахождение радиуса окружности требует знания формулы и умения применять ее в задачах. С помощью решения приведенных выше примеров задач ты можешь лучше понять, как это делается.