Mathcad – это мощное программное обеспечение, используемое для математических и инженерных расчетов. Одной из важных задач, которую можно решить с помощью Mathcad, является нахождение пересечений функции с осями координат.
Чтобы найти пересечение функции с осью абсцисс, необходимо решить уравнение f(x) = 0, где f(x) – заданная функция. Для этого в Mathcad используется команда solve. Например, если задана функция f(x) = x^2 - 4, чтобы найти пересечение с осью абсцисс, нужно ввести команду solve(x^2 - 4 = 0). Выполнив эту команду, Mathcad найдет решение уравнения и выведет его результат на экран.
Аналогично, чтобы найти пересечение функции с осью ординат, нужно найти значение функции, при котором x = 0. Для этого в Mathcad используется команда subst. Например, пусть задана функция f(x) = 3x + 2. Чтобы найти пересечение с осью ординат, необходимо ввести команду subst(0, x, 3x + 2). Mathcad выполнит эту команду и выведет значение функции при x = 0.
Таким образом, с помощью Mathcad можно легко и быстро найти пересечения функции с осями координат. Это полезное умение при работе с математическими моделями и анализе данных. Mathcad позволяет проводить сложные вычисления и находить решения уравнений с минимальными усилиями.
Определение пересечения функции с осью абсцисс
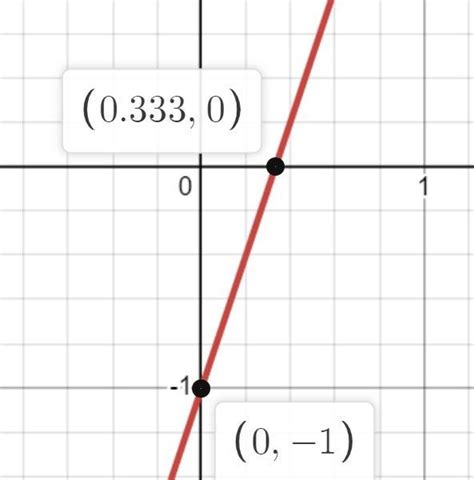
Когда мы говорим о пересечении функции с осью абсцисс, мы имеем в виду точки, в которых значение функции равно нулю. То есть, это моменты, когда график функции пересекает ось абсцисс в некоторых точках.
Для определения таких точек, в Matcad можно использовать различные методы. Один из самых простых и популярных методов - это решение уравнения функции относительно x. Если у нас есть функция f(x), то мы можем найти значения x, при которых f(x) = 0.
Чтобы это сделать, мы можем использовать краткую запись в Matcad, используя оператор "=" и указывая равенство f(x) = 0. Затем нужно решить это уравнение относительно x. Для решения можно использовать встроенную функцию solve(). Например, если у нас есть функция f(x) = x^2 - 4, мы можем записать уравнение x^2 - 4 = 0 и решить его с помощью solve().
| Функция | Уравнение | Пересечение с осью абсцисс |
|---|---|---|
| f(x) = x^2 - 4 | x^2 - 4 = 0 | x = -2, x = 2 |
Однако, если у нас есть сложная функция или уравнение, то может быть полезно использовать численные методы для нахождения пересечений. В Matcad есть множество встроенных численных методов, таких как метод Ньютона или метод деления пополам. Эти методы позволяют приближенно найти значения x, при которых функция пересекает ось абсцисс.
В зависимости от сложности функции и требуемой точности, можно выбрать наиболее подходящий метод для нахождения пересечений. При использовании численных методов следует учитывать, что они не всегда гарантируют точное решение, особенно если у функции есть множество пересечений.
В итоге, определение пересечения функции с осью абсцисс в Matcad может быть выполнено с помощью решения уравнения f(x) = 0 или численных методов. Выбор метода зависит от сложности функции и требуемой точности.
Способы определения пересечения функции с осью ординат
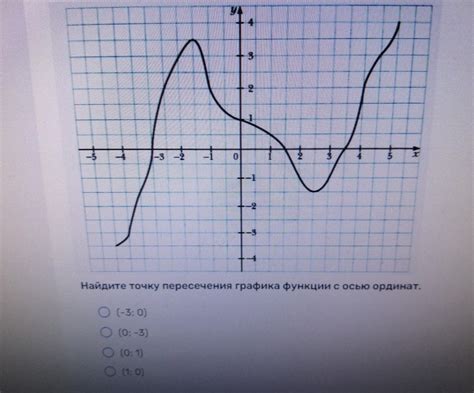
Наиболее распространенным способом определения пересечения функции с осью ординат является решение уравнения функции, приравнивая ее значение к нулю. Другими словами, нам нужно найти корни уравнения функции, которые и будут являться точками пересечения с осью ординат. Для этого можно воспользоваться различными методами, такими как метод бисекции, метод Ньютона и др.
Более простым способом определения пересечения функции с осью ординат является построение графика функции и нахождение точек пересечения с осью ординат на графическом представлении функции. Для этого можно использовать специальные программы, такие как Mathcad, которые позволяют строить графики функций с высокой точностью.
Иногда пересечение функции с осью ординат может быть очевидным, например, если функция имеет нулевой свободный член или содержит слагаемые с противоположными знаками. В таких случаях достаточно проанализировать функцию аналитически и определить, когда она равна нулю.
Итак, для определения пересечения функции с осью ординат можно использовать решение уравнения функции, графическое представление функции или аналитический анализ функции. Какой способ выбрать зависит от конкретной функции и предпочтений исследователя.
Использование графического метода для поиска пересечений
Для использования графического метода в Matcad необходимо выполнить следующие шаги:
- Задать функцию, пересечение которой с осью координат требуется найти. Для этого можно использовать формулы, заданные с помощью операций и функций Matcad.
- Построить график функции на основе заданных формул. Для этого в Matcad используется встроенная функция plot.
- Анализировать полученный график и находить точки пересечения с осью координат. Пересечение графика с осью X означает, что значение Y равно 0, а пересечение с осью Y означает, что значение X равно 0.
- Записывать найденные точки пересечения в виде пар координат (X, Y).
Использование графического метода для поиска пересечений позволяет получить визуальное представление о поведении функции и определить точки, в которых она пересекает оси координат. Этот метод удобен в случае, когда нет возможности или необходимости использовать аналитические методы для нахождения точек пересечения функции с осями.
Важно помнить, что графический метод можно применять только для задач, в которых функция имеет непрерывные значения и не имеет особых точек, таких как вершины, перегибы и разрывы.
Применение аналитического метода для определения пересечений
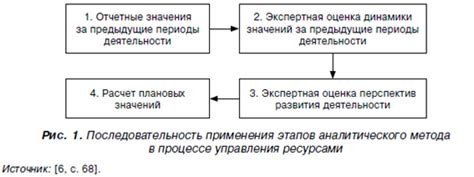
Для нахождения пересечений функции с осью x необходимо приравнять выражение, задающее функцию, к нулю и решить полученное уравнение относительно x. Таким образом, полученные значения x являются абсциссами точек пересечений функции с осью x.
Аналогично, для нахождения пересечений функции с осью y необходимо приравнять выражение, задающее функцию, к нулю и решить полученное уравнение относительно y. После решения уравнения полученные значения y являются ординатами точек пересечений функции с осью y.
Аналитический метод позволяет определить все пересечения функции с осями координат и получить полную информацию о значении абсциссы и ординаты каждой точки пересечения.
Применение аналитического метода для определения пересечений функции с осями координат позволяет более точно изучить поведение функции в разных областях и задать исследование функции в тех точках, которые наиболее важны с точки зрения анализа функциональных свойств.
Практический пример: нахождение пересечений функции с осями координат
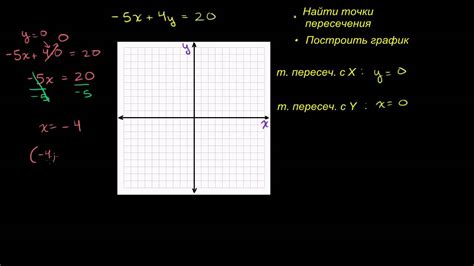
Допустим, у нас есть функция f(x), заданная на интервале от a до b. Наша задача состоит в нахождении точек пересечения этой функции с осями координат.
Для начала, нам необходимо построить график функции f(x) на данном интервале. Для этого, мы можем воспользоваться функцией plot в Matcad. Затем, мы должны определить точки пересечения графика с осями координат.
Существует два случая пересечения: пересечение с осью абсцисс (ось X), когда значение функции равно нулю, и пересечение с осью ординат (ось Y), когда значение аргумента равно нулю.
Начнем с поиска точек пересечения графика функции с осью абсцисс. Для этого, нам нужно решить уравнение f(x) = 0. Мы можем использовать функцию solve в Matcad для нахождения корней этого уравнения.
Затем, рассмотрим пересечение с осью ординат. Для этого, мы должны найти значение аргумента x, при котором значение функции f(x) равно нулю. То есть, нам нужно решить уравнение f(x) = 0 для переменной x.
Итак, мы рассмотрели практический пример: нахождение пересечений функции с осями координат. Для этого, нам потребовалось построить график функции, определить точки пересечения с осью абсцисс и осью ординат, и решить соответствующие уравнения.