Установить значения функции на концах отрезка является одной из важных задач в математике. Это позволяет нам определить поведение функции на заданном интервале. Зная значения функции на концах отрезка, мы можем более точно анализировать ее свойства и использовать эту информацию для решения различных задач.

Существует несколько способов найти значения функции на концах отрезка. Один из самых простых и распространенных способов - подстановка значений граничных точек в уравнение функции. Например, если у нас есть функция f(x) = 2x + 1, и нам нужно найти значения функции на отрезке [-1, 2], мы можем подставить -1 и 2 вместо x и рассчитать соответствующие значения f(-1) = 2(-1) + 1 = -1 и f(2) = 2(2) + 1 = 5.

Еще один способ найти значения функции на концах отрезка - построить график функции и определить точки пересечения с осями координат. Если функция пересекает ось OX в точке (a, 0), то значение функции на левом конце отрезка будет равно f(a), а значение на правом конце - f(b), где b - правая граница отрезка.

Определение значений функции на концах отрезка имеет большое значение в анализе функций и решении задач из различных областей. Аналитический и графический подходы позволяют нам более полно понять и использовать свойства функций на заданном интервале. Используйте эти методы, чтобы уточнить значения функции на концах отрезка и получить ценную информацию для вашего исследования или задачи.

Понятие и задача

Для решения многих задач, связанных с анализом функций, важно знать значения функции на концах отрезка. Это позволяет определить поведение функции в начале и конце отрезка, а также выявить особенности и закономерности в ее изменении.

Определение значений функции на концах отрезка является одной из основных задач анализа функций. Для этого необходимо подставить значения, соответствующие концам отрезка, в уравнение функции и вычислить полученные результаты.

Задача определения значений функции на концах отрезка актуальна во многих областях, включая математику, физику, экономику и программирование. При решении задач, связанных с определением экстремумов, нахождением нулей функции и анализом ее поведения, знание значений функции на концах отрезка играет важную роль.

Графическое решение

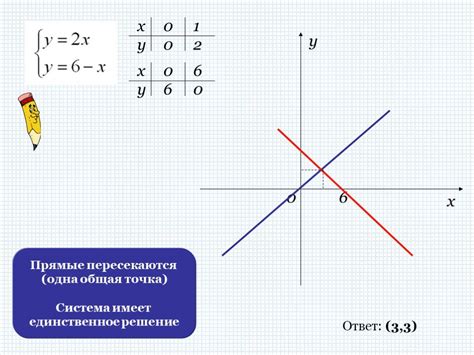
Для нахождения значения функции на концах отрезка можно использовать графический метод.

1. Постройте график функции, представляющей собой линию на координатной плоскости.
2. Изучите поведение графика функции на всем отрезке.
3. Найдите точку, соответствующую началу отрезка и определите значение функции в этой точке.
4. Точно так же найдите точку, соответствующую концу отрезка и определите значение функции в этой точке.

Итак, мы получили две точки на графике функции, соответствующие началу и концу отрезка. Значения функции в этих точках будут являться значениями функции на концах отрезка.

Таким образом, графическое решение позволяет найти значения функции на концах отрезка, используя график функции и его поведение на этом отрезке.

Аналитическое решение

Для нахождения значений функции на концах отрезка можно использовать аналитическое решение. Аналитическое решение заключается в выражении функции в явном виде и подстановке граничных значений в эту формулу.

Если функция задана аналитически, то можно использовать это свойство для нахождения ее значений на концах отрезка. Подстановка конечных значений отрезка в аналитическое выражение позволяет получить точное значение функции в этих точках.

Например, пусть функция задана выражением f(x) = 2x - 3. Для нахождения значений функции на концах отрезка [a, b], нужно подставить значения a и b в формулу функции:

Если a = 1 и b = 5, то:

f(1) = 2*1 - 3 = -1

f(5) = 2*5 - 3 = 7

Таким образом, значения функции на концах отрезка [1, 5] равны -1 и 7 соответственно.

Аналитическое решение позволяет получить точные значения функции на концах отрезка без использования графиков или численных методов.

Примечание: Для применения аналитического решения необходимо знать аналитическую форму функции, либо иметь возможность выразить функцию в аналитическом виде.

Пример задачи

Рассмотрим следующую задачу:

Найти значения функции f(x) = 2x^2 - 3x + 1 на концах отрезка [1, 5].

Для решения этой задачи, необходимо подставить значения концов отрезка в функцию и вычислить соответствующие значения:

Для x = 1:

f(1) = 2(1)^2 - 3(1) + 1 = 2 - 3 + 1 = 0

Для x = 5:

f(5) = 2(5)^2 - 3(5) + 1 = 50 - 15 + 1 = 36

Таким образом, значения функции на концах отрезка равны 0 и 36 соответственно.

Полезные советы и рекомендации

Когда необходимо найти значения функции на концах отрезка, следует учесть несколько важных моментов, которые помогут избежать ошибок и получить точные результаты.

1. Внимательно ознакомьтесь с заданным отрезком и функцией, чтобы понять их особенности и свойства. Это поможет определить возможные значения на концах.

2. Исследуйте поведение функции на всем промежутке отрезка, чтобы выявить особенности и переходы функции через точки разрыва.

3. Обратите внимание на асимптоты функции и их связь с концами отрезка. Они могут помочь определить значения на этих точках.

4. При необходимости, воспользуйтесь графическим представлением функции или графическими калькуляторами для более точного нахождения значений на концах отрезка.

5. Учтите правила и свойства данной функции, чтобы определить возможные значения на границах отрезка. Например, если функция монотонно возрастает на всем отрезке, то максимальное значение будет находиться на правом конце отрезка.

6. При наличии разрывов или особых точек, учтите их при определении значений функции на концах отрезка. Возможно, придется разбить отрезок на несколько частей для правильного анализа и нахождения значений.

Используя эти советы и рекомендации, вы сможете точно определить значения функции на концах отрезка и выполнить нужные вычисления без ошибок.