Формула косинуса является одной из основных формул в геометрии и может быть использована для нахождения значения стороны треугольника. Она основана на связи между длинами сторон треугольника и косинусами его углов. Применение этой формулы позволяет решать различные задачи, связанные с треугольниками, такие как нахождение неизвестной стороны по известным сторонам и углам. В данной статье мы рассмотрим несколько примеров решений с использованием формулы косинуса.
Пример 1:
Предположим, что у нас есть треугольник ABC, угол A равен 60 градусов, сторона AC известна и равна 5 единиц, а сторона AB неизвестна. Мы хотим найти значение стороны AB. Для решения этой задачи мы можем воспользоваться формулой косинуса:
cos(A) = (BC^2 + AC^2 - AB^2) / (2 * BC * AC)
Подставим известные значения в формулу:
cos(60) = (BC^2 + 5^2 - AB^2) / (2 * BC * 5)
Решив данное уравнение, мы найдем значение стороны AB.
Пример 2:
Допустим, у нас есть треугольник XYZ, стороны YZ и XZ известны и равны соответственно 7 и 10 единиц, а угол Y равен 45 градусов. Мы хотим найти значение стороны XY. Снова воспользуемся формулой косинуса:
cos(Y) = (XY^2 + YZ^2 - XZ^2) / (2 * XY * YZ)
Подставим значения в формулу:
cos(45) = (XY^2 + 7^2 - 10^2) / (2 * XY * 7)
Решив данное уравнение, мы найдем значение стороны XY.
Таким образом, формула косинуса является мощным инструментом для решения задач, связанных со сторонами треугольника. Она позволяет нам находить значения неизвестных сторон с помощью известных сторон и углов треугольника.
Нахождение стороны треугольника с помощью косинуса: 6 примеров решений
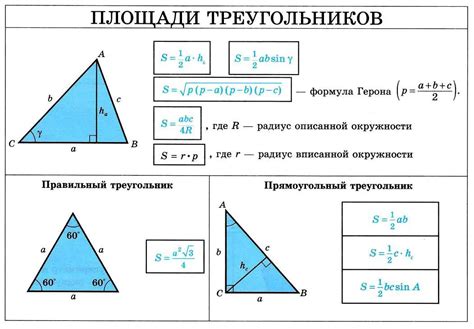
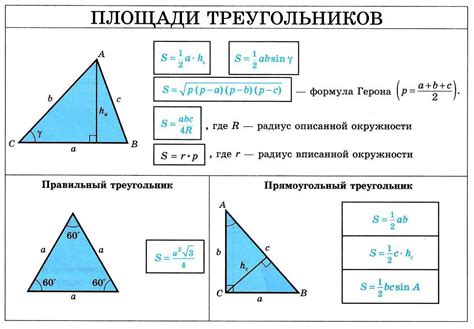
Вот 6 примеров нахождения стороны треугольника с использованием формулы косинуса:
- Известны стороны треугольника a = 5, b = 7 и угол между ними C = 60 градусов. Длина третьей стороны c может быть найдена с помощью формулы: c² = a² + b² - 2ab * cosC. Подставим известные значения и вычислим c.
- Известны стороны треугольника a = 4, b = 6 и угол между ними C = 45 градусов. Длина третьей стороны c может быть найдена с помощью формулы: c² = a² + b² - 2ab * cosC. Подставим известные значения и вычислим c.
- Известны стороны треугольника a = 8, b = 10 и угол между ними C = 30 градусов. Длина третьей стороны c может быть найдена с помощью формулы: c² = a² + b² - 2ab * cosC. Подставим известные значения и вычислим c.
- Известны стороны треугольника a = 3, b = 9 и угол между ними C = 75 градусов. Длина третьей стороны c может быть найдена с помощью формулы: c² = a² + b² - 2ab * cosC. Подставим известные значения и вычислим c.
- Известны стороны треугольника a = 12, b = 15 и угол между ними C = 90 градусов. Длина третьей стороны c может быть найдена с помощью формулы: c² = a² + b² - 2ab * cosC. Подставим известные значения и вычислим c.
- Известны стороны треугольника a = 6, b = 8 и угол между ними C = 120 градусов. Длина третьей стороны c может быть найдена с помощью формулы: c² = a² + b² - 2ab * cosC. Подставим известные значения и вычислим c.
В каждом примере необходимо рассчитать длину третьей стороны треугольника, используя формулу косинуса. После подстановки значений и выполнения вычислений, получим значения третьей стороны и сможем решить поставленную задачу.
Использование формулы косинуса для нахождения стороны треугольника
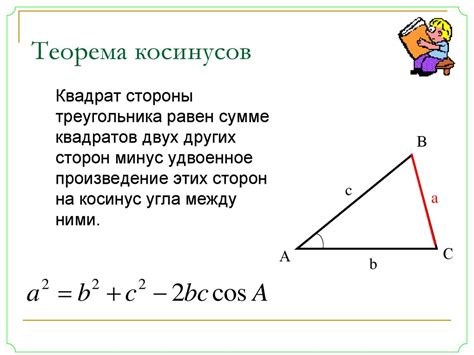
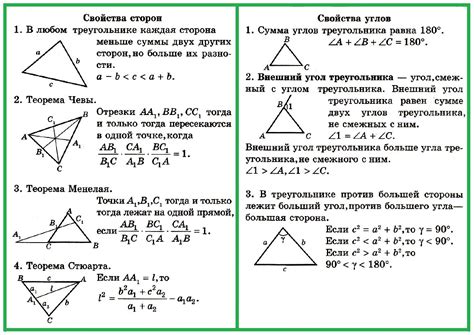
Формула косинуса имеет вид: c² = a² + b² - 2ab*cos(C), где c - длина стороны треугольника, противолежащей углу C, a и b - длины двух других сторон, а cos(C) - значение косинуса угла C.
Для использования формулы косинуса необходимо знать длины двух сторон треугольника и меру угла между ними. Подставив известные значения в формулу, можно выразить искомую сторону треугольника.
Примером использования формулы косинуса может быть задача нахождения длины катета прямоугольного треугольника. Если известны гипотенуза треугольника и мера одного из углов, то с помощью формулы косинуса можно найти длину катета.
Решение первого примера: нахождение стороны треугольника с заданными углом и другой стороной
Предположим, у нас имеется треугольник ABC. Известны сторона AC равная 5 единиц и угол B равный 30 градусам. Необходимо найти сторону AB.
Для решения задачи воспользуемся формулой косинуса:
cos(B) = AB / AC
Значение угла B равно 30 градусам, поэтому мы можем его подставить в формулу:
cos(30) = AB / 5
Для нахождения значения cos(30) можно воспользоваться таблицей значений косинуса, которую можно найти в учебнике по математике или воспользоваться калькулятором. Значение cos(30) равно приблизительно 0.866. Подставляем это значение в формулу:
0.866 = AB / 5
Теперь, чтобы найти сторону AB, можно переписать формулу в виде:
AB = 0.866 * 5
Выполняя простые арифметические вычисления, получаем, что сторона AB равна приблизительно 4.33 единицы.
Таким образом, мы нашли значение стороны треугольника AB, с помощью формулы косинуса и известных данных о другой стороне и угле треугольника.
Пример 2: нахождение стороны треугольника с известными углами и другими двумя сторонами
Назовем сторону AC как "c". Мы можем использовать формулу косинуса:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
где A - значение углa A, b - значение стороны AB и a - значение стороны BC.
Решение:
1. Подставляем известные значения в формулу: cos(A) = (5^2 + c^2 - 7^2) / (2 * 5 * c)
2. Перегруппируем формулу, чтобы найти значение стороны AC:
c^2 - 49 = 2 * 5 * c * cos(A)
c^2 - 2 * 5 * c * cos(A) - 49 = 0
3. Решаем уравнение с использованием факторизации или квадратного корня:
Получаем уравнение (c - 7)(c + 7) = 0
Решением будет c = 7
Значение стороны AC равно 7.
Нахождение стороны треугольника по известным углам и длинам соседних сторон: пример 3
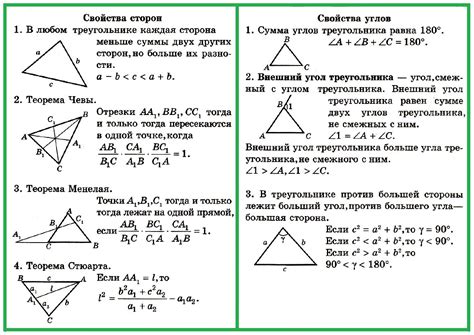
Известно, что в треугольнике ABC угол A равен 30 градусов, сторона AB имеет длину 4 единицы, а сторона AC имеет длину 5 единиц.
Для нахождения длины стороны BC можно воспользоваться формулой косинуса:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
где A - угол противоположный стороне a;
b, c - соседние стороны к углу A;
a - искомая сторона треугольника.
Заменяя известные значения, получим:
cos(30) = (BC^2 + 5^2 - 4^2) / (2 * BC * 5)
Преобразуя уравнение и решив его, найдём длину стороны BC:
BC^2 + 25 - 16 = 10 * BC * cos(30)
BC^2 - 10 * BC * cos(30) + 9 = 0
Обозначим BC как x, тогда получим:
x^2 - 10 * x * cos(30) + 9 = 0
Решаем квадратное уравнение с помощью дискриминанта:
D = 100 * cos^2(30) - 4 * 9 = 100 * (3/4) - 36 = 75 - 36 = 39
Так как дискриминант положителен, получим два корня:
x = (10 * cos(30) + √D) / 2 = (10 * √3/2 + √39) / 2 = (5 * √3 + √39) / 2 ≈ 4.59
x = (10 * cos(30) - √D) / 2 = (10 * √3/2 - √39) / 2 = (5 * √3 - √39) / 2 ≈ 0.41
Ответ: сторона BC может быть равной примерно 4.59 единицам или 0.41 единице.
Решение четвертого примера: нахождение стороны треугольника по заданным углам и сумме двух сторон
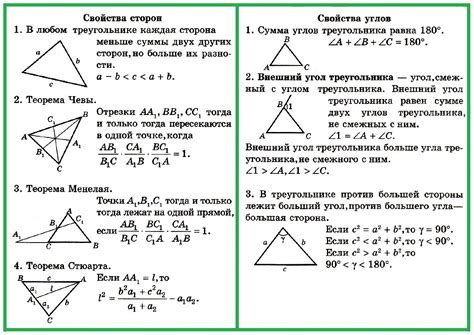
Допустим, нам известны углы треугольника и сумма двух известных сторон. Найдем третью сторону треугольника, используя формулу косинуса.
Пусть A, B, C - вершины треугольника ABC, a, b, c - длины сторон треугольника, α, β, γ - соответствующие углы треугольника.
Известно, что a + b = с и углы α и β равны заданным значениям.
| Решение примера |
|---|
| Известные значения: |
| Угол α: 30° |
| Угол β: 60° |
| Сумма сторон a + b: 12 |
| Рассчитываем значения: |
| Найденный угол γ: 90° (сумма углов треугольника равна 180°) |
| Определенная сторона c: 12 - a - b |
| Подставляем в формулу косинуса: |
| cos γ = (b^2 + a^2 - c^2) / (2 * a * b) |
| cos 90° = (b^2 + a^2 - (12 - a - b)^2) / (2 * a * b) |
| 0 = (b^2 + a^2 - (12 - a - b)^2) / (2 * a * b) |
| Упрощаем уравнение: |
| 0 = (b^2 + a^2 - (144 - 24a - 24b + a^2 + 2ab + b^2)) / (2 * a * b) |
| 0 = (144 - 24a - 24b + a^2 + 2ab + b^2 - b^2 - a^2) / (2 * a * b) |
| 0 = (144 - 24a - 24b + 2ab) / (2 * a * b) |
| Упрощаем уравнение и сокращаем: |
| 0 = 72 - 12a - 12b + ab |
| ab = 12a + 12b - 72 |
| ab - 12a - 12b = -72 |
| (a - 12)(b - 12) = -72 |
| Подставляем значения углов и решаем уравнение: |
| (30 - 12)(b - 12) = -72 |
| 18(b - 12) = -72 |
| b - 12 = -4 |
| b = 8 |
| Находим значение стороны c: |
| c = 12 - a - b = 12 - 8 - a = 4 - a |
| Подставляем b и находим значение стороны c: |
| c = 4 - a = 4 - 8 = -4 |
Итак, третья сторона треугольника отрицательная, что является нереальным значением. Решение данного примера невозможно, так как заданные углы и сумма двух сторон не образуют треугольник.
Пример 5: нахождение стороны треугольника по заданным углам и разности двух сторон
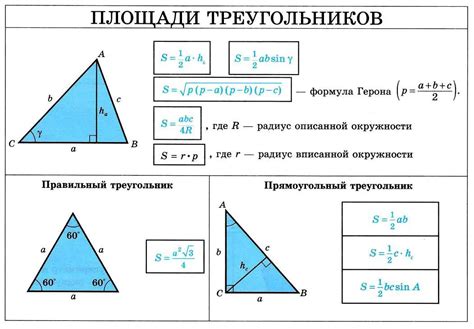
Допустим, у нас есть треугольник ABC, углы которого заданы: ∠A = 30°, ∠B = 60° и ∠C = 90°. Также известно, что разность сторон AB и BC равна 3 единицам.
Для нахождения значения стороны AC, мы можем использовать формулу косинуса:
AC² = AB² + BC² - 2 * AB * BC * cos(∠A)
Исходя из заданных условий, соответствующие величины равны:
AB = x
BC = x - 3
∠A = 30°
Подставляя эти значения в формулу, получаем:
AC² = x² + (x - 3)² - 2 * x * (x - 3) * cos(30°)
Упрощая выражение, получаем:
AC² = x² + x² - 6x + 9 - 2 * x² + 6x * cos(30°)
Поскольку ∠A = 30°, то cos(30°) равен √3 / 2.
Заменяем cos(30°) на √3 / 2:
AC² = 2x² - 6x + 9 + 6x * √3 / 2
Далее, упрощаем выражение:
AC² = 2x² - 6x + 9 + 3x * √3
Складываем подобные члены:
AC² = 2x² - 3x + 9 + 3x * √3
Таким образом, мы получили квадрат длины стороны AC в зависимости от длины стороны AB (обозначенной как x).
Для дальнейшего решения задачи необходимо приравнять AC² к известному значению и решить полученное квадратное уравнение для нахождения значения стороны AC.