Ноль в степени ноль - это одна из самых непонятных и спорных математических формул. Исторически, вопрос об этом выражении вызывал множество разногласий среди ученых. Степень нуля породила множество дискуссий и споров в течение многих веков.
Однако, теперь мы можем сказать с уверенностью, что ноль в степени ноль равно один. Результат данной формулы был рассмотрен и доказан учеными с использованием различных математических методов и теорий. Ответ на этот вопрос основывается на строгих математических принципах и логике.
Здесь следует отметить, что ответ не является интуитивным. Интуитивно может показаться логичным, что ноль возводится в любую степень, должно быть равно нулю. Однако, математические методы позволяют понять, что в реальности результат выражения "ноль в степени ноль" равен единице.
Таким образом, эта формула стала одной из излюбленных головоломок и примеров в математической науке. Мы разобрались в ней и теперь можем быть уверены в правильности ответа. Ноль в степени ноль равно один - и это уже точно установленный факт в современной математике.
Понятие "Ноль в степени ноль"
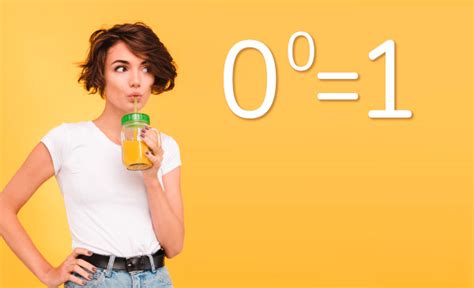
Однако, при возведении нуля в ноль степень, возникают определённые противоречия и неопределённости. Существуют различные точки зрения на то, что должно быть результатом этой операции.
Одни математики утверждают, что ноль в степени ноль должен быть равен единице. Это обусловлено тем, что при делении единицы на себя мы получаем единицу, а при возведении числа в ноль, оно должно равняться единице.
Другие математики считают, что ноль в степени ноль не имеет определённого значения и является неопределённой формой. Они рассматривают этот случай как граничный и оставляют его без присвоения точного значения.
Однако, несмотря на разногласия, большинство математических соглашений и согласования признают ноль в степени ноль равным единице. Это правило используется в различных математических дисциплинах и имеет свое обоснование в теории комбинаторики и анализа функций.
Таким образом, вопрос о значении нуля в степени ноль остаётся актуальным и вызывает дискуссии среди ученых и математиков по всему миру.
История степеней в математике

Одним из первых математиков, который начал работать с понятием степени, был греческий ученый Архимед. В III веке до нашей эры он использовал степени для решения различных математических задач.
В средние века арабские математики, в особенности Мухаммед аль-Хорезми, сделали большой вклад в развитие степеней. Они создали алгебраические методы для работы со степенями, включая вычисление и использование их свойств.
Европейские математики вплоть до XVII века продолжали исследовать степени и разрабатывать новые методы для их работы. Одним из ключевых вкладов в эту область была работа Рене Декарта, который использовал степени для решения уравнений.
В последующие века понятие степеней продолжало развиваться и находить свое применение в различных областях науки и техники. Сейчас степени являются основой многих математических и физических теорий.
Использование степеней в математике позволяет упростить вычисления, работать с большими числами и решать сложные задачи. Правила работы со степенями дают возможность удобно записывать и решать математические уравнения и неравенства.
Интересный факт: ноль в степени ноль равно один - это одно из спорных математических утверждений, которое ведет к дискуссиям и разным интерпретациям.
В итоге, степени играют важную роль в математике и имеют множество приложений в реальном мире. Они позволяют упростить и структурировать сложные математические процессы и помогают понять и описать множество явлений и закономерностей.
Что означает "ноль в степени ноль"
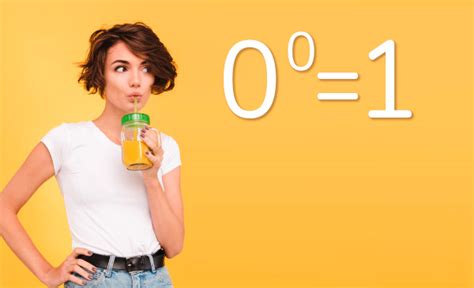
Однако, существует аргументация, поддерживающая различные варианты результата. Некоторые математики и физики считают, что ноль в степени ноль должен равняться единице. Это обусловлено определением любой величины, возведенной в ноль, равной единице.
Другие же утверждают, что ноль в степени ноль должен быть равен нулю. Это объясняется свойствами нуля, который в любой степени дает ноль.
Существуют также математические и физические проблемы, которые вызывают споры относительно значения нуля в степени ноль. Нуль в степени ноль возникает при рассмотрении предела, функций и рядов. В этих случаях его значение определяется контекстом задачи.
Независимо от того, какое значение вы присваиваете нулю в степени ноль, важно помнить, что это не обычное числовое значение, а специальный случай, который интерпретируется по ситуации и имеет свои особенности.
Какие разночтения возникают при вычислении "ноля в степени ноль"

Некоторые математики считают, что ноль в степени ноль равно единице, поскольку существует несколько математических доводов в пользу этой идеи. Например, по определению, любое число в степени ноль равно единице, поэтому ноль в степени ноль должен быть равен единице. Кроме того, ноль в степени ноль может использоваться в различных областях математики, таких как комбинаторика и теория множеств.
Тем не менее, существуют также аргументы против вычисления нуля в степени ноль. Некоторые математики считают, что выражение не имеет определения и является неопределенным. Они указывают на то, что возвести ноль в степень ноль равносильно попытке разделить ноль на ноль, что не имеет смысла и не определено в математике. Также существуют случаи, когда ноль в степени ноль может привести к абсурдным результатам, что говорит в пользу того, что это выражение не имеет определения.
Таким образом, вопрос о вычислении нуля в степени ноль остается открытым и вызывает дискуссии среди математиков. Важно понимать, что разночтения по данному вопросу связаны с особенностями математической логики и контекстом, в котором это выражение используется. Поэтому в каждом конкретном случае необходимо учитывать соответствующие математические правила и определения.
Обсуждение и различные точки зрения на вопрос о результатах

Вопрос о результате возведения нуля в степень ноль долгое время являлся объектом обсуждения среди математиков и философов. Некоторые аргументируют, что в данном случае результат должен равняться единице. Они опираются на логическое рассуждение: любое число, возведенное в ноль, равно единице. Ноль в степени ноль должен быть исключением, но логический принцип остается применимым.
Однако, существует и альтернативная точка зрения. Критики данного результата отмечают, что ноль - это нейтральный элемент для умножения, который не меняет значение других чисел. Если результатом возведения нуля в степень ноль было бы единица, это противоречило бы свойствам нейтрального элемента и дестабилизировало бы математические формулы и операции, в которых нули и степени нуля присутствуют.
| Поддерживающие единицу | Альтернативные точки зрения |
|---|---|
| Логическое рассуждение | Нейтральный элемент нуль |
| Равенство другим возведениям в ноль | Дестабилизация математических операций |
| Универсальность и избегание исключений |
В конечном итоге, споры исчерпывающе не решены, и вопрос о результате возведения нуля в степень ноль остается открытым. Каждый специалист в математике может выбрать свою точку зрения в зависимости от того, какие аргументы ему кажутся убедительными.
Разбор примеров и иллюстрации

Для лучшего понимания формулы, давайте рассмотрим несколько примеров и проиллюстрируем их графически.
Пример 1:
Рассмотрим выражение 00. Если мы возводим число в степень, это означает, что мы умножаем это число само на себя заданное количество раз. Так, 02 будет равно 0*0 = 0, а 03 будет равно 0*0*0 = 0.
Теперь, если мы возведем 0 в степень 0, получим 0*0*0... бесконечное количество раз. Однако, любое число, умноженное на ноль, будет равно нулю. Поэтому, 0 в степени 0 представляет собой бесконечное произведение нулей, что в свою очередь равно 1.
Пример 2:
Рассмотрим выражение 10. Из предыдущего примера мы уже знаем, что любое число, возведенное в степень 0, равно 1. Поэтому, 1 в степени 0 равно 1.
Пример 3:
Рассмотрим выражение 01. Если мы возведем 0 в степень 1, это будет означать, что мы умножаем 0 само на себя 1 раз. В итоге, получаем 0*0 = 0. Таким образом, 0 в степени 1 равно 0.
Иллюстрация ниже показывает значения, к которым мы пришли после разбора примеров:
00 = 1
10 = 1
01 = 0
Теперь, когда мы разобрались в формуле и рассмотрели несколько примеров, мы можем уверенно сказать, что ноль в степени ноль равно одному.