Пересечение прямых – одна из основных задач в геометрии, которую необходимо решать во множестве прикладных областей, начиная от инженерии и заканчивая информационными технологиями. Более того, она остается актуальной и сегодня, при постоянном развитии техники и внедрении новых технологий. Конечно же, всем известен базовый метод решения данной задачи, однако существуют и другие способы, которые оказываются гораздо более эффективными и универсальными, особенно в случаях сложной геометрии.
Одним из таких способов является использование векторного подхода. Этот метод основан на представлении уравнений прямых в виде векторных уравнений, что позволяет абстрагироваться от исходных координат прямых и сосредоточиться на их направлениях. Применение векторов значительно упрощает решение задачи, особенно в случаях с перемещениями и поворотами прямых.
Кроме того, в последние годы стали популярными алгоритмы, основанные на машинном обучении. С их помощью можно разработать модель, которая самостоятельно сможет находить пересечение прямых, используя данные об их координатах и дополнительные параметры. Этот подход активно применяется в областях компьютерного зрения и обработки изображений, где точность и скорость решения играют ключевую роль для установления объектов на изображениях.
Эффективные советы и методы для нахождения пересечения прямых
При работе с геометрическими фигурами, в особенности с прямыми, возникает необходимость нахождения их пересечений. Правильное нахождение точек пересечения имеет большое значение при решении множества задач в различных областях науки и техники. В этом разделе мы рассмотрим несколько эффективных советов и методов, которые помогут вам упростить и ускорить процесс нахождения пересечения прямых.
1. Использование формулы пересечения
Наиболее простым и известным методом нахождения пересечения прямых является использование формулы пересечения. Формула позволяет легко вычислить координаты точки пересечения на основе уравнений прямых. Для этого необходимо подставить значения коэффициентов прямых в формулу и произвести вычисления.
2. Графическое представление
Графическое представление прямых позволяет визуально определить точки их пересечения. Для этого необходимо построить координатную плоскость и на ней отметить точки, соответствующие уравнениям прямых. Затем можно определить точку пересечения с помощью линейки или просто глазом.
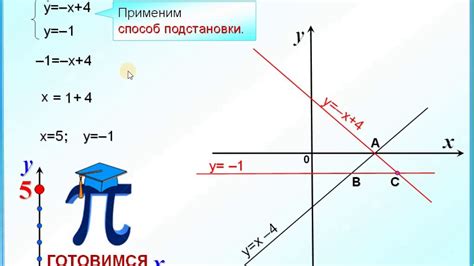
3. Метод подстановки
Ещё один простой и эффективный метод нахождения пересечения прямых - метод подстановки. Он заключается в подстановке значений координат точки пересечения в уравнения прямых. Если подставленные значения удовлетворяют уравнениям, то точка является точкой пересечения.
4. Использование матричных операций
Современные методы нахождения пересечения прямых основаны на использовании матричных операций. Такой подход позволяет решать задачи быстрее и эффективнее. Для этого необходимо представить уравнения прямых в матричной форме и использовать методы решения систем линейных уравнений для нахождения точки пересечения.
Используя эти эффективные советы и методы, вы сможете легко и быстро находить пересечение прямых в различных задачах. Каждый из предложенных методов имеет свои преимущества и может быть применен в зависимости от конкретной ситуации. Не бοйтесь экспериментировать и выбирать подход, наилучшим образом соответствующий вашим требованиям.
Метод Гаусса для нахождения пересечения прямых

Для начала, система уравнений, задающая прямые, записывается в матричной форме, где каждая строка матрицы соответствует уравнению прямой:
| a1 | b1 | c1 |
| a2 | b2 | c2 |
Где a1 и b1 - коэффициенты при x и y первой прямой, a2 и b2 - коэффициенты при x и y второй прямой, c1 и c2 - свободные члены.
Затем, применяя операции элементарного преобразования, систему уравнений можно привести к улучшенному ступенчатому виду, где коэффициенты перед неизвестными убывают слева направо и сверху вниз.
Наконец, решая полученную систему методом обратной подстановки, найденные значения для неизвестных x и y представляют собой координаты точки пересечения прямых.
Метод графического решения для нахождения пересечения прямых

Для начала, необходимо задать уравнения двух прямых, которые нужно пересечь. Обычно уравнения прямых записывают в виде y = kx + b, где k - коэффициент наклона прямой, а b - свободный член. Как только уравнения прямых известны, следует нарисовать их графики на одной координатной плоскости.
Далее необходимо внимательно проанализировать полученные графики. Пересечение прямых будет точкой координат (x, y), в которой они пересекаются. Определить координаты этой точки достаточно просто: нужно обратить внимание на точку, где графики прямых пересекаются на плоскости. Координаты этой точки будут искомыми значениями x и y.
Однако следует отметить, что метод графического решения является приближенным и может быть неточным, особенно в случае, если прямые параллельны или совпадают. В таких случаях пересечение может быть неоднозначным или не существовать вовсе.
Использование уравнений прямых для нахождения их пересечения

У каждой прямой есть уравнение вида y = mx + b, где m – коэффициент наклона, а b – коэффициент смещения. Для того чтобы найти точку пересечения двух прямых, необходимо приравнять их уравнения и решить получившуюся систему уравнений.
Например, пусть у нас есть две прямые с уравнениями:
прямая 1: y = 2x + 3
прямая 2: y = -4x + 5
Чтобы найти точку пересечения, мы должны приравнять уравнения двух прямых:
2x + 3 = -4x + 5
Затем решаем получившуюся уравнение для x:
6x = 2
x = 1/3
Подставляем найденное значение x обратно в одно из уравнений и находим y:
прямая 1: y = 2 * (1/3) + 3 = 2/3 + 9/3 = 11/3
Итак, точка пересечения прямых равна (1/3, 11/3).
Таким образом, использование уравнений прямых позволяет найти точку их пересечения с помощью решения системы уравнений и подстановки значений.
Использование формулы нахождения координат пересечения прямых

Существует несколько способов нахождения координат пересечения прямых:
- Метод подстановки. В этом методе мы подставляем выражение y одного уравнения в другое и находим значение x. Затем подставляем найденное значение x в любое из уравнений и находим значение y.
- Метод комбинирования. В этом методе мы вычитаем одно уравнение из другого, чтобы получить выражение только с переменной x. Затем решаем полученное уравнение для x и подставляем найденное значение в любое из исходных уравнений для нахождения y.
- Метод определителей. В этом методе мы составляем систему уравнений с двумя уравнениями и двумя неизвестными x и y. Затем используем правило Крамера для нахождения значений x и y.
Выбор метода зависит от конкретной задачи и уравнений прямых. Важно помнить, что при расчете координат пересечения прямых необходимо учитывать особенности каждого метода и выполнять все необходимые действия для нахождения точного решения.
Применение метода Крамера для нахождения пересечения прямых

Шаги для применения метода Крамера:
- Запишите уравнения прямых в параметрической форме. Например, прямая А задается как x = x1 + at, y = y1 + bt, а прямая B задается как x = x2 + cu, y = y2 + du; где (x1, y1) и (x2, y2) – координаты точек на каждой прямой, а a, b, c, d – параметры;
- Составьте матрицу системы уравнений, в которой каждая строка соответствует уравнению прямой, а столбцы содержат коэффициенты при переменных x, y, t и u;
- Вычислите определитель основной матрицы системы уравнений. Он равен определителю матрицы, в которой вместо столбца коэффициентов при x, y, t и u используются столбцы свободных членов;
- Вычислите определители матриц, полученных заменой столбцов коэффициентов при x, y, t и u на столбцы свободных членов. Они равны определителю основной матрицы системы, но в них заменены строки, соответствующие каждому уравнению;
- Решите получившуюся систему из четырех уравнений относительно a, b, c и d, используя формулы Крамера. Они выражаются через определители второго шага. Например, a = D1/D, b = D2/D, где D1, D2 и D – определители, вычисленные на третьем шаге;
- Подставьте найденные значения параметров a, b, c и d в одно из уравнений изначальной системы и найдите значения переменных t и u;
- Подставьте найденные значения t и u в параметрические уравнения прямых и вычислите значения x и y точки пересечения прямых.
Использование метода Крамера позволяет эффективно и точно находить пересечение двух прямых. Он широко применяется в различных областях, таких как математика, физика, инженерия и компьютерная графика.
Аналитическое решение для нахождения пересечения прямых

При решении задачи нахождения пересечения прямых аналитическим методом, можно воспользоваться системой уравнений для двух прямых:
| Уравнение прямой 1: | y = k1x + b1 |
| Уравнение прямой 2: | y = k2x + b2 |
Для нахождения точки пересечения (x0, y0) необходимо решить систему уравнений:
| k1x + b1 = k2x + b2 |
| (k1 - k2)x = b2 - b1 |
| x = (b2 - b1) / (k1 - k2) |
Подставив значение x в любое из уравнений прямых, найдем y:
| y = k1(b2 - b1) / (k1 - k2) + b1 |
| y0 = (k1b2 - k2b1) / (k1 - k2) |
Таким образом, мы получаем точку пересечения прямых с координатами (x0, y0). Этот метод является одним из самых точных и эффективных способов нахождения пересечения прямых.