Умножение является одной из основных операций арифметики, и она используется для выполнения различных математических задач. Умножение позволяет нам находить произведение двух или более чисел, что в свою очередь помогает нам решать множество задач различной сложности.
Существует несколько способов решения задач с помощью умножения, каждый из которых может быть применим в определенной ситуации.
Во-первых, умножение может использоваться для нахождения площади прямоугольника или квадрата. Для этого нужно умножить длину на ширину фигуры. Например, если у нас есть прямоугольник с длиной 5 см и шириной 3 см, мы можем найти его площадь, умножив 5 на 3, что даст нам 15 см^2.
Во-вторых, умножение может быть использовано для нахождения общей стоимости при покупке нескольких одинаковых товаров. Для этого нужно умножить цену одной единицы товара на количество единиц. Например, если одно яблоко стоит 2 рубля, и мы хотим купить 6 яблок, мы можем умножить 2 на 6 и получим общую стоимость в 12 рублей.
В-третьих, умножение может быть применено для нахождения периметра прямоугольника или квадрата. Для этого нужно умножить сумму всех сторон на 2. Например, если прямоугольник имеет стороны 4 см и 6 см, мы можем найти его периметр, умножив (4 + 6) на 2, что даст нам 20 см.
Как видно из этих примеров, умножение является весьма полезной операцией, которая позволяет нам решать разнообразные задачи и находить ответы на них. Необходимость умножения становится особенно очевидной в повседневной жизни и при решении математических задач.
Применение умножения в решении задач

1. Расчет площади прямоугольника
Площадь прямоугольника можно вычислить, умножив длину одной стороны на длину другой стороны. Формула для расчета площади прямоугольника выглядит следующим образом: S = a * b, где S - площадь, a - длина одной стороны, b - длина другой стороны. Например, если стороны прямоугольника равны 4 и 6 единиц, то его площадь будет равна 24 единицы.
2. Подсчет общей стоимости товаров
При покупке нескольких товаров с разными ценами умножение может быть использовано для расчета общей стоимости. Для этого необходимо умножить цену каждого товара на его количество и сложить результаты. Например, при покупке 3 товаров по 10, 15 и 20 единиц каждый, общая стоимость будет равна 10*3 + 15*3 + 20*3 = 105 единиц.
3. Вычисление процента от числа
Умножение также может быть использовано для вычисления процента от числа. Для этого необходимо умножить число на процент, поделить результат на 100 и полученное значение будет являться процентом от исходного числа. Например, если нужно найти 20% от числа 150, то необходимо выполнить следующие вычисления: 150 * 20 / 100 = 30.
4. Решение пропорций
Умножение широко используется для решения пропорций. Пропорция - это уравнение, в котором две дроби равны друг другу. Для решения пропорции можно использовать правило трех или простое умножение. Например, если известно, что 2 см соответствуют 5 мм, то для определения длины 7 см нужно умножить 7 на 5 и поделить на 2, что даст результат 7 * 5 / 2 = 17.5 мм.
Умножение является мощным инструментом, который широко применяется для решения различных задач в разных сферах. Знание и понимание применения умножения поможет более эффективно решать задачи и находить точные ответы.
Расчет площади фигур
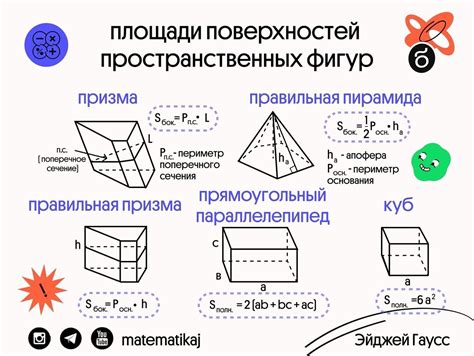
Площадь прямоугольника равна произведению его длины и ширины. Для прямоугольника со сторонами a и b, его площадь можно вычислить по формуле:
Площадь = a * b
Площадь квадрата равна квадрату его стороны. Для квадрата со стороной a, его площадь можно вычислить по формуле:
Площадь = a * a
Площадь треугольника равна половине произведения его основания и высоты. Для треугольника с основанием a и высотой h, его площадь можно вычислить по формуле:
Площадь = 0.5 * a * h
Расчет площади круга производится по формуле:
Площадь = π * r * r
где π (пи) - это математическая константа, приближенное значение которой равно 3.14, а r - радиус окружности.
Эти формулы помогают нам вычислить площадь различных фигур и применить эти знания в решении различных задач, таких как ремонт, строительство, архитектура и многое другое.
Вычисление цены за несколько единиц товара
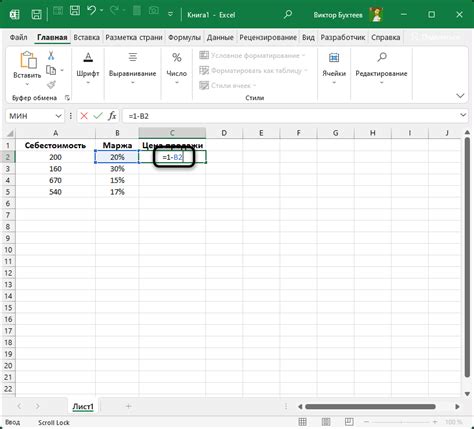
Допустим, у нас есть товар, стоимость которого равна Х рублей за одну единицу. И нам необходимо вычислить общую стоимость за N единиц этого товара. Для этого мы можем воспользоваться операцией умножения.
Для начала, мы можем умножить стоимость одной единицы товара на количество единиц, чтобы получить общую стоимость:
Общая стоимость = Х * N
Например, если одна единица товара стоит 100 рублей, и нам нужно купить 5 единиц, мы можем вычислить общую стоимость следующим образом:
Общая стоимость = 100 * 5 = 500 рублей
Таким образом, чтобы вычислить стоимость за несколько единиц товара, нам необходимо умножить стоимость одной единицы на количество единиц.
Определение времени прохождения расстояния

Для определения времени прохождения расстояния мы можем использовать формулу:
Время = Расстояние / Скорость
Здесь время указывается в единицах времени (например, секундах или часах), расстояние - в единицах длины (например, метрах или километрах), а скорость - в единицах длины на единицу времени (например, метрах в секунду или километрах в час).
Для примера, допустим, что мы знаем, что расстояние, которое нужно пройти, равно 100 метрам, а скорость, с которой движется объект, составляет 10 метров в секунду. Чтобы определить время прохождения расстояния, мы можем подставить эти значения в формулу:
Время = 100 м / 10 м/с = 10 секунд
Таким образом, время прохождения расстояния равно 10 секундам.
Эта формула может быть использована для определения времени прохождения расстояния в различных ситуациях, будь то движение пешехода, автомобиля, поезда или другого объекта.
Оценка количества материала на строительных объектах
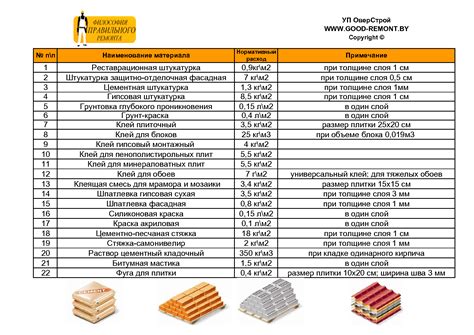
Использование математических формул
Одним из самых распространенных способов оценки количества материала является использование математических формул. Например, для определения площади стен или пола можно использовать формулу площади прямоугольника: S = a * b, где a и b - длины сторон. Для определения объема материала можно использовать формулу объема прямоугольного параллелепипеда: V = a * b * h, где a, b и h - длины сторон.
Использование технической документации
Для более точной оценки количества материала можно использовать техническую документацию, такую как чертежи, проекты и спецификации. На основе этих документов можно определить не только геометрические характеристики объекта, но и требования к материалам, их расход и нормативы.
Использование специальных программ
Современные технологии позволяют использовать специальные программы и онлайн-калькуляторы для оценки количества материала на строительных объектах. Эти программы учитывают не только геометрические характеристики объекта, но и другие факторы, такие как тип материала, его плотность, свойства и т.д. Такой подход позволяет получить наиболее точную оценку расхода материала.
Система единиц измерения
При оценке количества материала важно также учитывать систему единиц измерения. Например, в России часто используется система метрических единиц измерения, таких как квадратные метры и кубические метры. Однако в некоторых случаях могут использоваться другие системы единиц измерения, например, американская система футов и дюймов. При оценке необходимо быть внимательным и использовать соответствующие формулы и коэффициенты перевода.
| Параметр | Значение |
|---|---|
| Высота стены | 3 метра |
| Ширина стены | 5 метров |
| Толщина стены | 0.3 метра |
| Расход кирпича на квадратный метр | 100 штук |
| Общий расход кирпича | 1500 штук |
Прогнозирование роста прибыли
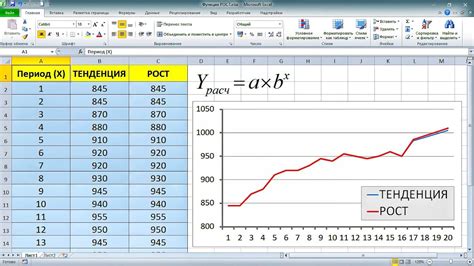
Один из методов прогнозирования роста прибыли - использование умножения. Принцип такого подхода заключается в умножении текущей прибыли на предполагаемый коэффициент роста. Этот коэффициент может быть определен на основе анализа прошлых показателей, рыночных условий и других факторов.
Для примера, предположим, что текущая прибыль компании составляет 100 000 долларов, а прогнозируемый коэффициент роста составляет 1.5. Тогда прогнозируемая прибыль будет равна 150 000 долларов (100 000 * 1.5).
Важно отметить, что использование умножения для прогнозирования роста прибыли имеет свои ограничения. Например, оно не учитывает возможные изменения внешних факторов, таких как экономические или политические условия, которые могут влиять на доходность компании. Поэтому рекомендуется использовать этот метод в комбинации с другими подходами, чтобы получить более точные и надежные прогнозы.
| Текущая прибыль | Прогнозируемый коэффициент роста | Прогнозируемая прибыль |
|---|---|---|
| 100 000 долларов | 1.5 | 150 000 долларов |
Определение количества продуктов для мероприятий
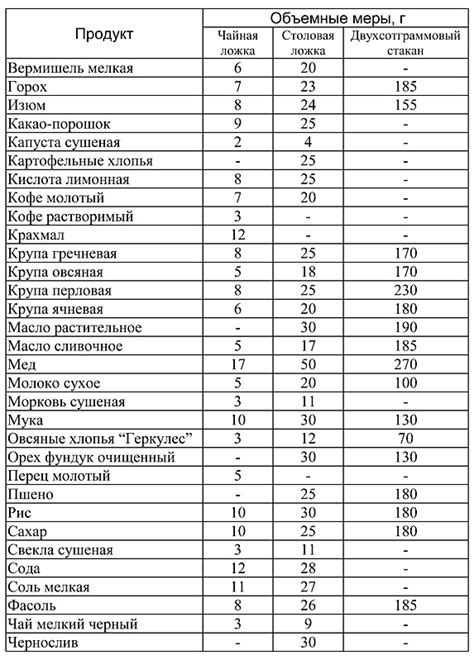
Прежде чем рассмотреть примеры применения умножения, важно установить несколько элементов:
| 1. | Тип мероприятия - определите, о каком мероприятии идет речь, так как разные мероприятия могут иметь различные потребности в продуктах. Например, на свадьбе может быть больше гостей, чем на корпоративной встрече, и потребуется больше еды и напитков. |
| 2. | Количество участников - определите, сколько человек примут участие в мероприятии. Это позволит определить общий объем продуктов, которые могут понадобиться. |
| 3. | Меню - определите, какие продукты будут предложены на мероприятии. Например, учитывайте блюда, напитки, десерты и закуски, указывая не только тип продукта, но и его количество. |
Один из способов определить количество продуктов - это умножить количество участников на количество продуктов, которое требуется для каждого. Например, если на вечеринке ожидается 50 гостей, а каждый гость требует одну бутылку вина, общее количество бутылок вина будет 50 * 1 = 50. Этот метод прост и прямолинеен в использовании.
Однако, чтобы получить более точные результаты, необходимо учитывать особенности каждого мероприятия и предусмотреть возможные дополнительные расходы, такие как дополнительная еда и напитки из-за продолжительности мероприятия или потерь из-за неожиданных ситуаций.
В итоге, умножение является полезным инструментом для определения количества продуктов для мероприятий, но необходимо учитывать различные факторы, чтобы избежать недостатка или избытка продуктов.
Оценка затрат на топливо для автомобиля
Затраты на топливо = Пробег x Расход топлива x Стоимость топлива
Для рассчета затрат на топливо необходимо знать несколько важных факторов. Пробег - это расстояние, которое автомобиль проезжает за определенный период времени, например, за месяц или за год. Расход топлива - это количество топлива, которое автомобиль потребляет на единицу пройденного расстояния, обычно измеряется в литрах на 100 километров или в милях на галлон. Стоимость топлива - это цена за единицу топлива, обычно измеряется в денежных единицах (рублях, долларах и т.д.)
Например, если автомобиль проехал 1000 километров, имеет расход топлива 8 литров на 100 километров и стоимость топлива составляет 50 рублей за литр, то затраты на топливо можно рассчитать следующим образом:
Затраты на топливо = 1000 км x 8 л/100 км x 50 руб/л = 40 000 рублей
Таким образом, оценка затрат на топливо для автомобиля может быть произведена с помощью простой математической операции умножения.
Подсчет времени работы робота
Допустим, роботу требуется 5 минут на выполнение одного действия, а он должен выполнять это действие 10 раз. Чтобы определить общее время работы робота, необходимо умножить время одного действия на количество действий:
Время работы робота = время одного действия × количество действий
В данном случае:
Время работы робота = 5 минут × 10 действий = 50 минут
Таким образом, общее время работы робота составит 50 минут.
Умножение позволяет легко и быстро подсчитывать время работы робота, если известно время выполнения одного действия и количество действий. Этот метод особенно полезен при решении задач, связанных с автоматизацией процессов и оптимизацией времени работы.



