Равносторонний треугольник – это особый вид треугольника, у которого все стороны равны друг другу. В геометрии он также известен, как треугольник с равными углами. Этот тип треугольника привлекает внимание своей симметричной и сбалансированной формой, вызывая интерес и удивление у людей.
Доказательства равносторонних треугольников являются важной и интересной частью изучения геометрии. Задача заключается в том, чтобы убедиться, что все три стороны треугольника равны между собой. Для этого необходимо применять различные геометрические методы и принципы.
В данной статье мы рассмотрим основные принципы доказательства равносторонних треугольников, такие как равенство углов, свойства равных сторон и связь с равнобедренными треугольниками. Также мы представим несколько примеров и задач, чтобы продемонстрировать применение этих принципов на практике.
Доказательство равносторонности треугольника

Доказательство через длины сторон
Один из самых простых способов доказательства равносторонности треугольника - это показать, что все его стороны имеют одинаковую длину. Для этого можно использовать измерительный инструмент, например, линейку, или применить методы измерения длины сторон, такие как теорема Пифагора.
Для доказательства можно замерить все три стороны треугольника и убедиться, что они равны между собой. Если все три стороны имеют одинаковую длину, то треугольник является равносторонним.
Доказательство через углы
Другой способ доказательства равносторонности треугольника - это показать, что все его углы равны между собой. Для этого можно использовать такие геометрические свойства, как сумма углов треугольника или свойства равных уголов.
Если все углы треугольника равны между собой и равны 60 градусов, то треугольник является равносторонним.
Доказательство через свойства равносторонних треугольников
Также можно использовать свойства уже известных равносторонних треугольников для доказательства равносторонности другого треугольника. Например, если известно, что две стороны одного треугольника равны двум сторонам другого треугольника, а угол между этими сторонами также равен, то эти треугольники будут равносторонними.
Важно помнить, что доказательство равносторонности треугольника должно быть основано на проверяемых фактах и логических рассуждениях. Кроме того, можно использовать геометрические инструменты, такие как геометрические построения или теоремы, чтобы упростить и объяснить доказательство.
Принципы равностороннего треугольника
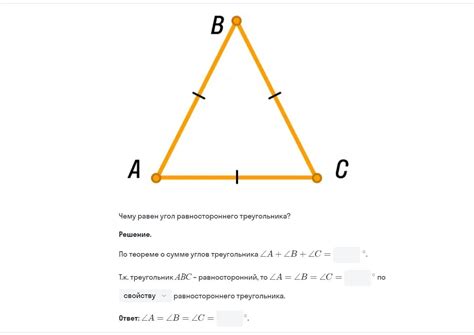
Одним из следствий принципа равенства сторон в равностороннем треугольнике является равенство всех трех углов треугольника. В равностороннем треугольнике все углы равны между собой и составляют 60 градусов каждый. Это свойство позволяет делать доказательства и решать геометрические задачи, основываясь на равности углов треугольника.
Для равностороннего треугольника также характерно равенство высот, биссектрис и медиан. Все высоты равностороннего треугольника равны между собой, все биссектрисы равны, а все медианы также равны. Это свойство позволяет производить расчеты и пользоваться геометрическими формулами, которые основаны на равенстве данных линий.
Использование принципов равностороннего треугольника является важным инструментом в геометрическом анализе. Они позволяют решать задачи, доказывать теоремы и производить расчеты, сокращая время и трудозатраты. Понимание принципов равностороннего треугольника помогает лучше разобраться в самой структуре треугольников и использовать эту информацию для решения геометрических задач.
Равные стороны и углы равностороннего треугольника
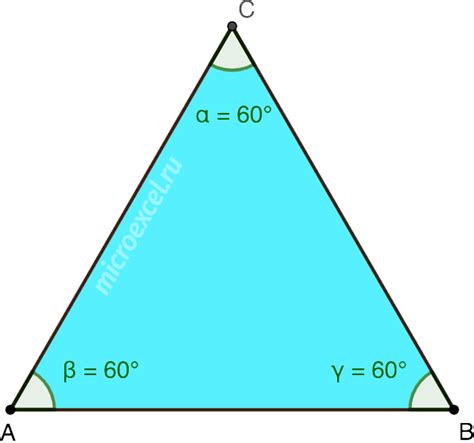
Ключевое свойство равностороннего треугольника - равность всех его сторон. Это свойство позволяет нам легко вычислять длину стороны треугольника, если известна длина одной из его сторон. Для этого можно использовать формулу:
длина второй стороны = длина первой стороны
длина третьей стороны = длина первой стороны
Равенство углов в равностороннем треугольнике также позволяет нам легко вычислять их величину. Так, если один из углов равен 60 градусов, то все остальные углы также будут равны 60 градусам.
Помимо этого, равные стороны и углы равностороннего треугольника играют важную роль в его свойствах и доказательствах. Например, равные стороны позволяют нам легко найти высоту и медианы треугольника, а также применять различные теоремы и формулы, основанные на равных сторонах и углах.
Таким образом, знание равных сторон и углов равностороннего треугольника позволяет нам более глубоко понять его свойства и использовать их при решении различных задач и задач.
Основные свойства равностороннего треугольника
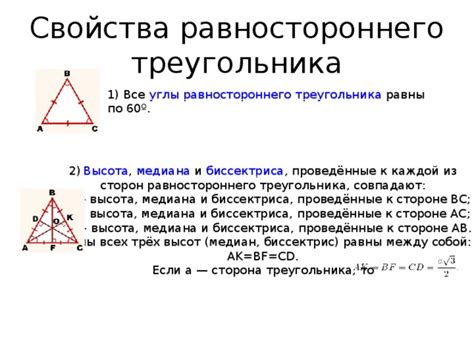
| 1. | Все углы равны 60 градусов |
| 2. | Высота, проведенная из вершины треугольника, является биссектрисой и медианой одновременно |
| 3. | Центр окружности, описанной около треугольника, совпадает с центром равностороннего треугольника |
| 4. | Площадь равностороннего треугольника можно вычислить по формуле: S = (√3 / 4) * a², где a - длина стороны треугольника |
Зная эти основные свойства, можно применять их для доказательства различных утверждений и теорем о равносторонних треугольниках. Например, по свойству 3 можно сказать, что радиус окружности, описанной вокруг равностороннего треугольника, равен половине длины любой стороны треугольника.
Доказательство равенства сторон равностороннего треугольника
| Утверждение | Объяснение |
|---|---|
| Строим равносторонний треугольник | Проводим построение, где все три стороны равны |
| Обозначение сторон | Обозначаем стороны треугольника как AB, BC и CA |
| Рассмотрение сторон | Рассматриваем стороны одну за другой: |
| AB = BC | В равностороннем треугольнике все стороны равны, поэтому AB равно BC |
| BC = CA | Аналогично, сторона BC равна стороне CA |
| CA = AB | А также сторона CA равна стороне AB |
| Заключение | Из вышеперечисленного следует, что все три стороны равностороннего треугольника AB, BC и CA равны между собой |
Таким образом, доказано равенство сторон в равностороннем треугольнике. Это свойство является одним из основных принципов и определений равностороннего треугольника.
Примеры равносторонних треугольников в природе
Равносторонний треугольник, у которого все три стороны равны между собой, можно встретить не только в математике, но и в различных объектах природы. Эти треугольники обладают особыми свойствами и часто находятся в симметричных формах.
Примером равностороннего треугольника в природе является снежинка. У снежинки есть шестиугольная симметрия, благодаря которой ее внешний вид напоминает равносторонний треугольник. Кристаллы снега, как правило, имеют шестиугольную симметрию благодаря особым условиям формирования во время замерзания влаги.
Еще одним примером равностороннего треугольника в природе является химическое соединение борнаит. Борнаит - это редкий минерал, образованный из бората натрия. Кристаллическая структура борнаита обладает равносторонней симметрией, что делает его прекрасным примером равностороннего треугольника в природе.
Также можно упомянуть равносторонние треугольники, которые образуются в колониях одного из видов муравьев - рабочих муравьев листорезов. Они строят свои гнезда в форме равностороннего треугольника, что позволяет им оптимально использовать пространство и эффективно охранять свое жилище от внешних угроз.
Это только некоторые примеры равносторонних треугольников в природе. Равносторонние треугольники являются одной из самых гармоничных и симметричных форм в природе, и мы можем встретить их повсюду, от малейших кристаллов до больших масштабов в природных явлениях.
Равносторонние треугольники в архитектуре и искусстве
В архитектуре равносторонние треугольники могут использоваться в качестве базовых элементов в строительстве. Они помогают создавать крепкие и устойчивые конструкции, благодаря равным углам и сторонам. Некоторые исторические памятники, такие как пирамиды и обелиски, имеют форму равностороннего треугольника и являются впечатляющими примерами использования этой геометрической формы.
В искусстве равносторонние треугольники могут служить креативным решением для создания гармоничной композиции. Они часто используются в оптических иллюзиях и живописи для создания впечатления глубины и перспективы. Равносторонний треугольник может быть символом баланса и гармонии, и его использование в произведениях искусства может придавать им особый смысл и эстетическое значение.
Интересно отметить, что равносторонние треугольники также имеют свои мистические и символические значения в различных культурах. В направлении зодиака равносторонний треугольник может олицетворять силу, гармонию и совершенство. Разные религии и древние цивилизации использовали равносторонний треугольник в своих символах и обрядах, привлекая энергию и баланс.
Таким образом, равносторонние треугольники играют важную роль и в архитектуре, и в искусстве. Их использование помогает создавать красивые и гармоничные формы, а также придавать произведениям особый смысл и эстетическое значение.
Использование равносторонних треугольников в геометрических задачах
Во-первых, равносторонний треугольник обладает свойством всех его углов быть равными 60 градусов. Это позволяет использовать его для нахождения углов в других треугольниках. Если мы знаем, что второй треугольник имеет одну сторону, равную стороне равностороннего треугольника, то мы можем найти значения углов второго треугольника, используя свойство того, что сумма углов в треугольнике равна 180 градусов.
Во-вторых, равносторонний треугольник может быть использован для нахождения высоты или медианы другого треугольника. Если мы проведем медиану или высоту треугольника, проходящую через вершину равностороннего треугольника, то она будет равна одной из его сторон. Это свойство позволяет нам использовать равносторонний треугольник для нахождения некоторых длин в других треугольниках.
Также равносторонние треугольники могут быть использованы для нахождения площади других треугольников. Если мы знаем, что одна из сторон треугольника равна стороне равностороннего треугольника, то мы можем использовать формулу площади треугольника (полупериметр умноженный на радиус вписанной окружности), где радиус вписанной окружности к равностороннему треугольнику будет равен половине его стороны.
Использование равносторонних треугольников в геометрических задачах позволяет упростить вычисления, сократить количество шагов и получить более точные результаты. Это мощный инструмент, который помогает нам лучше понять и решать различные геометрические задачи.