Определитель матрицы – это число, которое вычисляется для квадратной матрицы и содержит информацию о линейной зависимости или независимости ее строк (или столбцов). Изменение строк в определителе является одной из стратегий, которые могут быть применены для упрощения вычислений и обнаружения особых свойств матрицы.
Оправданность изменения строк в определителе – это вопрос, который вызывает жаркие дискуссии среди математиков. Некоторые специалисты утверждают, что подобные изменения могут привести к неверным результатам и искажению информации о матрице. В то же время, другие аргументируют, что подходящие изменения строк могут помочь сделать вычисления более простыми или выявить закономерности, скрытые в исходной матрице.
Основная проблема состоит в том, что изменение строк в определителе может привести к изменению значения определителя самой матрицы. Поэтому необходимо быть крайне осторожным и оценивать влияние такого действия на результаты вычислений. В некоторых случаях, изменения могут быть допустимыми и даже полезными, особенно если они приводят к упрощению вычислений или экономии времени. Однако в других случаях, изменение строк может привести к серьезным ошибкам и некорректным результатам.
Изменение строк в определителе: принимаемое решение или лишнее действие?

Принятие решения об изменении строк в определителе – это сложный и неоднозначный выбор, который требует от нас внимательного и взвешенного подхода. Во-первых, мы должны понять, какое влияние это изменение окажет на определитель и его свойства. Если изменение внесет существенные коррективы и приведет к новым значениям определителя, то, безусловно, такое решение будет принято с особой осторожностью.
С другой стороны, есть ситуации, когда изменение строк в определителе может быть безопасным и даже необходимым действием. Например, при вычислении определителя большой матрицы часто применяют метод Гаусса для приведения его к треугольному виду. В этом случае изменение строк матрицы в процессе решения задачи является неотъемлемой частью алгоритма решения и не влияет на корректность полученного ответа.
Также следует заметить, что иногда изменение строк в определителе может привести к противоречивым или несостоятельным результатам. Например, при случайном перемещении строк местами мы можем получить некорректное значение определителя, что повлечет за собой ошибочное решение задачи или неверный результат.
Итак, ответ на вопрос о том, является ли изменение строк в определителе принимаемым решением или лишним действием, зависит от конкретной ситуации и целей, которые мы преследуем. Важно помнить, что внесение изменений в определитель может существенно повлиять на его свойства и значения, поэтому такое решение необходимо принимать с осторожностью и основываясь на анализе задачи и математических методов, применяемых для ее решения.
Определитель и его значимость

Значимость определителя состоит в том, что он позволяет нам решать системы линейных уравнений, вычислять обратные матрицы, находить собственные значения и векторы матрицы, а также выполнять многие другие математические операции.
Кроме того, определитель используется для определения площади и объёма параллелепипеда, определения ориентации поверхности и много других геометрических задач.
Таким образом, можно с уверенностью сказать, что определитель является неотъемлемой частью математики, которая находит применение во многих областях науки и техники. Его значимость и практическая применимость делает его важным инструментом для различных исследований и решения сложных математических задач.
Оправданность изменения строк в определителе

Часто при работе с матрицами возникает необходимость изменить порядок строк или столбцов исходной матрицы, а затем вычислить определитель полученной матрицы. Оправданность таких изменений в определителе определяется правилами линейной алгебры и зависит от конкретного контекста и задачи.
При изменении порядка строк в матрице, определитель меняет свой знак. Если в исходной матрице строки i и j меняются местами, то определитель полученной матрицы будет равен минус определителю исходной матрицы.
Иногда изменение порядка строк в определителе может иметь существенное значение для решения задачи. Например, при решении системы линейных уравнений методом Крамера, необходимо вычислить определитель матрицы системы. Если явные зависимости между строками матрицы видны, можно менять порядок строк, чтобы получить более удобный вариант определителя и ускорить вычисления.
Однако в некоторых случаях изменение порядка строк может привести к ошибкам и некорректному результату. В основе правила изменения порядка строк лежит идея о связи между перестановками строк и перестановками компонентов определителя. При изменении порядка строк нужно быть внимательным и следить, чтобы перестановки не противоречили правилам формирования определителя.
Вычисление определителя с измененными строками
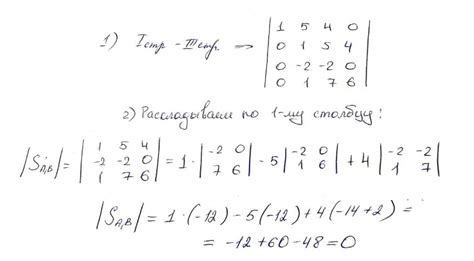
Перестановка строк в матрице может быть оправданной, если она позволяет легче вычислить определитель. Изменение строк может помочь упростить матрицу, вывести нули на побочную диагональ или сделать определитель треугольным.
Основное правило для изменения строк заключается в том, что меняется знак определителя при перестановке строк с четным числом инверсий, и остается без изменений при перестановке строк с нечетным числом инверсий.
Вычисление определителя с измененными строками может быть полезным инструментом для упрощения матрицы и улучшения понимания ее структуры. Однако, перед изменением строк необходимо тщательно анализировать матрицу и оценивать возможные последствия такого изменения.
Возможные ошибки при изменении строк
1. Ошибки в арифметике:
Использование неправильных знаков при вычислении нового значения определителя по измененным строкам может привести к неверным результатам. Например, неправильно примененный знак минус может изменить знак всего определителя.
2. Недостаточность информации:
Изменение строк в определителе может потребовать дополнительной информации о системе, например, о количестве строк или столбцов. Неправильно указанная информация может привести к неправильному искажению определителя.
3. Ошибки при изменении порядка строк:
Изменение порядка строк может привести к смещению значений в определителе, особенно если эти строки содержат нули или другие специфические значения. Неправильный порядок строк может внести путаницу и усложнить понимание определителя.
4. Неправильное применение операций:
Операции, примененные к измененным строкам в определителе, могут быть неправильно выбраны или неправильно применены. Например, неправильное применение операции сложения или вычитания может привести к неверным результатам и ошибочным действиям.
Для избежания указанных ошибок, необходимо внимательно анализировать и планировать каждое изменение строк в определителе, учитывая математические свойства и особенности задачи. Необходимо также аккуратно выполнять вычисления и проверять результаты, чтобы предотвратить возможные ошибки.
В процессе работы с определителем матрицы возникает вопрос о необходимости его изменения. Ответ на этот вопрос зависит от цели исследования или задачи, которую необходимо решить.
Если изменение определителя позволяет упростить вычисления или улучшить понимание сути математической модели, то принимать решение о его изменении оказывается обоснованным. Например, замена одной строки определителя на сумму двух строк может значительно упростить вычисления в случае, когда в двух строках находятся подобные слагаемые.
Однако не всегда изменение определителя является рациональным решением. Иногда, даже незначительное изменение может привести к искажению результата или потере важной информации. В таких случаях рекомендуется оставить определитель без изменений.
Таким образом, принимать решение о изменении определителя следует на основании анализа конкретной ситуации и учета целей исследования. В каждом отдельном случае необходимо взвешивать все возможные плюсы и минусы изменения определителя, и уже после этого принимать окончательное решение.
| За изменение определителя | Против изменения определителя |
|---|---|
| Упрощение вычислений | Риск искажения результата |
| Улучшение понимания модели | Потеря важной информации |