Координатная плоскость - это одно из основных понятий, используемых в математике. Она представляет собой двумерное пространство, на котором можно определить положение точек с помощью двух чисел, называемых координатами - абсциссы и ординаты.
Абсцисса точки на координатной плоскости - это первая координата, отвечающая за ее положение по горизонтальной оси. Определение абсциссы точки - это процесс нахождения значения этой координаты для заданной точки.
Одним из основных принципов определения абсциссы является использование системы координат. Для этого на координатной плоскости выбираются начало координат (обычно обозначается буквой O) и две перпендикулярные друг другу оси - горизонтальная (обозначается буквой х) и вертикальная (обозначается буквой у).
Методы определения абсциссы точки зависят от задачи и предоставленной информации. Основным методом является использование геометрических свойств фигур и координат точек, а также вычислений на основе математических формул. При решении задачи на определение абсциссы точки важно учитывать принципы арифметики и алгебры, чтобы получить корректный ответ.
Что такое абсцисса точки?

Абсцисса точки обозначается буквой x и может принимать положительные и отрицательные значения в зависимости от положения точки относительно начальной точки оси X. Таким образом, абсцисса точки определяет ее положение на плоскости относительно оси X.
| Точка | Абсцисса (x) | Ордината (y) |
|---|---|---|
| A | -2 | 3 |
| B | 0 | -1 |
| C | 4 | 0 |
Описание и примеры использования

Для определения абсциссы точки можем использовать следующие методы:
- Использование графического изображения на координатной плоскости, где необходимо найти положение точки на оси x;
- Применение формулы, которая связывает абсциссу точки с другими параметрами, такими как угол наклона прямой или расстояние между точками;
- Использование математических операций и свойств, таких как симметрия или пропорциональность, для определения абсциссы точки.
Примеры использования включают следующие ситуации:
- Найти абсциссу точки A на координатной плоскости с заданными координатами (3, 4);
- Определить абсциссу точки B, лежащей на прямой с углом наклона 45 градусов и проходящей через точку C(-2, 5);
- Рассчитать абсциссу точки D, которая симметрична точке E(2, -6) относительно оси x.
Определение абсциссы точки является важным элементом в математике и на практике используется для решения различных задач, таких как построение графиков функций, анализ движения тел в пространстве и определение геометрических свойств фигур.
Координатная плоскость: основные принципы
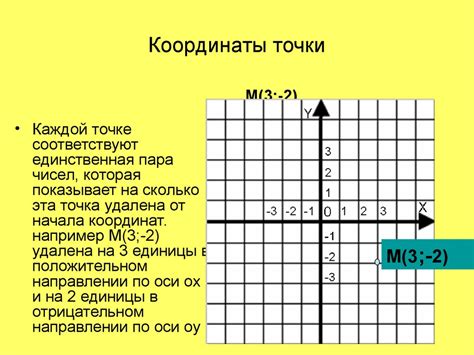
Основными принципами работы с координатной плоскостью являются:
| Принцип | Описание |
| Положительные и отрицательные числа | Отметки на оси абсцисс и ординат могут быть как положительными, так и отрицательными, в зависимости от положения точки относительно начала координат. |
| Прямые координатные оси | Оси абсцисс и ординат являются прямыми линиями, которые проходят через начало координат и простираются в обоих направлениях. |
| Система координат | Все точки на плоскости могут быть однозначно определены с помощью пары чисел (абсцисса, ордината). Это позволяет представить сложные геометрические фигуры в виде набора точек. |
Координатная плоскость является важным инструментом для решения задач из различных областей науки и инженерии, а также в геометрии и анализе данных. Понимание основных принципов работы с ней позволяет легче воспринимать и анализировать информацию, представленную на графиках и диаграммах.
Система координат и оси
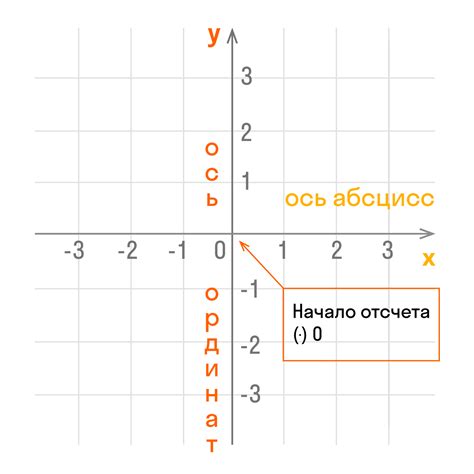
Горизонтальная ось разбивается на положительные и отрицательные числа, расположенные справа и слева от начала координат соответственно. Положительные числа на горизонтальной оси направлены вправо, а отрицательные числа - влево. Каждое число на горизонтальной оси соответствует некоторой абсциссе точки на плоскости.
Вертикальная ось также разбивается на положительные и отрицательные числа, расположенные над и под началом координат соответственно. Положительные числа на вертикальной оси направлены вверх, а отрицательные числа - вниз. Каждое число на вертикальной оси соответствует некоторой ординате точки на плоскости.
Таким образом, система координат позволяет однозначно задать положение точки на плоскости с помощью пары чисел (абсцисса, ордината). Абсцисса определяет положение точки относительно горизонтальной оси, а ордината - относительно вертикальной оси.
Правила определения абсциссы

Абсцисса точки на координатной плоскости представляет собой первую координату этой точки и обозначается буквой "х". Определение абсциссы выполняется в соответствии с определенными правилами.
1. Определение абсциссы точки на оси OX:
Для определения абсциссы точки, расположенной на оси OX, нужно обратить внимание на расстояние от этой точки до начала координатной плоскости. Абсцисса такой точки равна этому расстоянию со знаком:
Если точка находится правее начала координат, то ее абсцисса будет положительной.
Если точка находится левее начала координат, то ее абсцисса будет отрицательной.
Если точка совпадает с началом координат, то ее абсцисса будет равна нулю.
2. Определение абсциссы точки внутри или вне оси OX:
Для определения абсциссы точки, которая находится внутри или вне оси OX, нужно провести перпендикуляр из этой точки на ось OX и обратить внимание на точку пересечения перпендикуляра с осью OX. Абсцисса такой точки равна координате пересечения.
Если точка находится ниже оси OX, ее абсцисса будет положительной.
Если точка находится выше оси OX, ее абсцисса будет отрицательной.
3. Определение абсциссы точки по ее координатам:
Абсцисса точки также может быть определена по ее координатам. Для этого нужно обратить внимание на значение первой координаты точки. Это и будет абсцисса этой точки.
Например, если точка имеет координаты (5, 3), то ее абсцисса будет равна 5.
Правильное определение абсциссы точки позволяет точно определить ее положение на координатной плоскости и упростить работу с графиками и функциями.
Методы определения абсциссы точки

1. Графический метод. Для определения абсциссы точки с помощью графического метода необходимо построить координатную плоскость и отложить значение абсциссы точки по горизонтальной оси. Затем, используя подходящий инструмент (линейку, компас и т.д.), измерить расстояние от начала координат до точки на оси абсцисс. Это и будет значением абсциссы.
2. Аналитический метод. Для определения абсциссы точки с помощью аналитического метода необходимо знать координаты точки и применить соответствующую формулу. Например, для точки (х, у) абсцисса определяется просто как значение х.
3. Вычислительный метод. Для определения абсциссы точки с помощью вычислительного метода необходимо использовать вычислительный алгоритм. Этот метод обычно применяется в программировании и математических моделях, где точка представляется в виде объекта с координатами, и абсцисса вызывается по необходимости.
Использование разных методов определения абсциссы точки позволяет решать различные задачи и находить абсциссу точки в разных условиях и при различных ограничениях.
Графический метод

Для определения абсциссы точки с помощью графического метода необходимо построить перпендикуляр к оси абсцисс, проходящий через точку. Затем, с помощью линейки или циркуля построить отрезок от начала координат до перпендикуляра и измерить его длину. Полученное значение является абсциссой точки.
Графический метод удобен в использовании при решении задач геометрии, например, при нахождении расстояния между двумя точками на плоскости или при определении положения точки относительно осей координат.
Однако, для точного определения абсциссы точки с помощью графического метода необходимы навыки работы с геометрическими построениями и измерениями. Поэтому, при решении сложных задач рекомендуется использовать другие методы, такие как аналитический или численный методы определения абсциссы точки.
Аналитический метод

Аналитический метод определения абсциссы точки на координатной плоскости основан на использовании алгебраических уравнений. Для определения абсциссы точки можно воспользоваться двумя основными приемами: применение формулы нахождения абсциссы точки на прямой и решение систем уравнений.
Применение формулы нахождения абсциссы точки на прямой позволяет определить координату точки, зная уравнение прямой и ординату этой точки. Для этого необходимо подставить значение ординаты исследуемой точки в уравнение прямой и решить полученное уравнение относительно абсциссы.
Решение систем уравнений также может применяться для нахождения абсциссы точки. Для этого систему уравнений составляют из известных уравнений прямых и либо уравнения прямой, содержащей исследуемую точку, либо уравнения окружности, в которой лежит точка. Затем систему решают методом подстановки или методом Крамера, получая значения абсцисс и ординат точек пересечения.
| Плюсы | Минусы |
| Точность результатов | Не всегда возможно найти точное значение |
| Возможность использования в различных задачах | Требует знания алгебры и математического аппарата |
Аналитический метод позволяет более точно определить абсциссу точки на координатной плоскости, однако требует знания алгебраических уравнений и методов их решения.