Анализ данных - это один из ключевых инструментов для принятия взвешенных решений в современном мире. При проведении анализа данных одной из основных задач является определение частоты. Частота представляет собой количество раз, которое определенное событие или значение встречается в наборе данных.

Существует несколько методов, позволяющих определить частоту в данных. Один из самых распространенных методов включает использование гистограммы. Гистограмма - это графическое представление данных, где по оси абсцисс отображаются различные значения, а по оси ординат - их частоты. Частоты могут быть представлены в виде абсолютных значений или относительных частот, выраженных в процентах.

Другой способ определения частоты - использование таблицы сопряженности. Таблица сопряженности представляет собой кросс-таблицу, в которой значения данных пересекаются с категориями или условиями. Подсчет частоты производится путем подсчета количества значений, удовлетворяющих определенным условиям.

Методы определения частоты и анализа данных

Один из основных методов определения частоты является метод гистограмм. Гистограмма представляет собой графическое представление распределения данных по различным интервалам. Она помогает визуализировать и анализировать частоту и плотность данных.

Другой метод определения частоты - это метод группировки. Этот метод позволяет объединить данные в группы или интервалы, чтобы определить частоту по каждой группе. Такой подход облегчает анализ больших объемов данных и выявление основных трендов и закономерностей.

Помимо определения частоты, анализ данных также включает в себя различные методы статистического анализа. Одним из таких методов является расчет среднего значения. Среднее значение позволяет оценить среднюю величину данных и выявить нетипичные или выбросы.

Другой метод статистического анализа - это определение стандартного отклонения. Стандартное отклонение показывает, насколько сильно данные отклоняются от среднего значения. Оно позволяет оценивать разброс данных и выявлять аномалии.

Кроме того, для проведения анализа данных можно использовать корреляционный анализ. Он позволяет определить, есть ли связь между двумя или более переменными. Корреляционный анализ помогает выявить зависимости и установить степень влияния одной переменной на другую.

Использование статистических методов

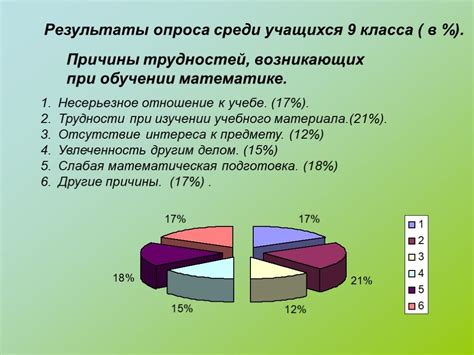
Одним из наиболее распространенных статистических методов является расчет частоты. Этот метод позволяет определить, как часто встречается определенное явление или событие в наборе данных. Для расчета частоты можно использовать различные статистические показатели, такие как абсолютная частота, относительная частота и др.

Кроме определения частоты, статистические методы позволяют провести анализ данных. С помощью статистического анализа можно выявить связи, зависимости и возможные тенденции в данных. Например, можно провести корреляционный анализ, который позволяет определить, есть ли статистическая связь между двумя переменными. Также можно провести регрессионный анализ для прогнозирования будущих значений на основе имеющихся данных.

Для использования статистических методов необходимо иметь соответствующие знания и навыки. Использование специализированного программного обеспечения, такого как статистические пакеты, может значительно облегчить проведение анализа данных. Но при этом следует помнить о необходимости правильной интерпретации полученных результатов и учета особенностей и ограничений используемых методов.

Применение методов машинного обучения

Одним из основных преимуществ применения методов машинного обучения является возможность автоматической обработки больших массивов данных. Процесс обучения модели машинного обучения начинается с предоставления ей размеченных данных, на основе которых модель "обучается" находить закономерности и прогнозировать значения в новых данных.

В случае определения частоты и проведения анализа данных, методы машинного обучения позволяют автоматически определить наиболее часто встречающиеся значения и их частоту. Для этого используются различные алгоритмы, такие как алгоритмы кластеризации, классификации или регрессии.

К примеру, для определения наиболее часто встречающегося слова в текстовом документе можно использовать алгоритм обработки естественного языка. Модель машинного обучения на основе обучающих данных будет искать закономерности и определять частоту каждого слова в документе.

Однако, для применения методов машинного обучения необходимо иметь размеченные данные, то есть данные, для которых известны правильные ответы или значения. Правильно подобранные данные итогового анализа помогут создать точную модель, способную определить частоту и провести анализ данных с высокой точностью.

Вычисление корреляции и регрессии

Для вычисления корреляции существуют различные методы, но наиболее распространенным является коэффициент корреляции Пирсона. Он измеряет степень линейной зависимости между двумя переменными и принимает значения от -1 до 1. Значение близкое к 1 означает положительную линейную зависимость, когда значения одной переменной возрастают, значения другой переменной также увеличиваются. Значение близкое к -1 означает отрицательную линейную зависимость, когда значения одной переменной возрастают, значения другой переменной уменьшаются. Значение близкое к 0 означает отсутствие линейной зависимости.

Регрессия представляет собой математическую модель, которая объясняет связь между зависимой переменной и одной или несколькими независимыми переменными. Наиболее распространенная форма регрессии - линейная регрессия, которая использует линейную функцию для предсказания значений зависимой переменной. Он может быть выражен уравнением y = mx + b, где y - зависимая переменная, x - независимая переменная, m - угловой коэффициент, b - свободный член.

Вычисление корреляции и регрессии полезно для многих задач анализа данных, таких как прогнозирование временных рядов, анализ финансовых данных, маркетинговые исследования и т.д. Они позволяют выявить зависимости между переменными и предсказывать значения на основе существующих данных.

Анализ временных рядов

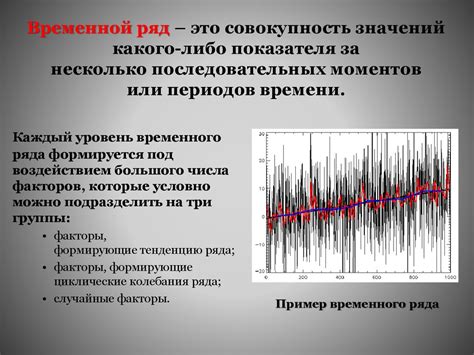
Основной шаг в анализе временных рядов - это определение частоты, с которой данные измеряются. Частота может быть ежечасной, ежедневной, еженедельной, ежемесячной и так далее. Она определяет, как часто данные собираются и записываются.

После определения частоты, можно провести анализ данных. Временные ряды могут быть визуализированы с помощью графиков, что позволяет увидеть общие тренды и сезонные колебания. Для поиска аномалий могут использоваться статистические методы или машинное обучение.

Важной частью анализа временных рядов является прогнозирование будущих значений. Для этого применяются различные модели, такие как авторегрессионные модели (AR), скользящие средние модели (MA), а также комбинации этих моделей (ARMA и ARIMA). Также можно использовать машинное обучение, например, нейронные сети или методы ансамблей.

Анализ временных рядов имеет много применений в различных областях, таких как финансовые рынки, метеорология, медицина, транспорт и многие другие. Надлежащий анализ временных рядов может помочь выявить закономерности, спрогнозировать будущие события и принять обоснованные решения.

Интерпретация результатов и принятие решений

Оценка результатов должна быть основана на всестороннем рассмотрении данных, их контексте и статистических методах, применяемых в анализе. Важно учесть различные факторы, которые могут повлиять на полученные результаты.

При интерпретации результатов, необходимо учитывать следующие аспекты:

1. Репрезентативность выборки: Если выборка, на основе которой был проведен анализ, не является достаточно представительной для целевой группы, то результаты могут быть неправильно интерпретированы. Необходимо учесть возможные искажения в выборке.
2. Статистическая значимость: Если полученные различия или связи не являются статистически значимыми, то результаты можно считать случайными. Уровень статистической значимости должен быть установлен заранее и принят во внимание при интерпретации результатов.
3. Практическая значимость: Помимо статистической значимости, важно также оценить практическую значимость полученных результатов. Необходимо задать себе вопрос, какая польза или важность может быть извлечена из данных и как они могут использоваться для принятия решений.

Интерпретация результатов и принятие решений в анализе данных является сложной задачей, требующей глубокого понимания статистических методов и контекста исследования. Важно быть внимательным и критическим к полученным результатам, а также учитывать их практическую значимость при принятии решений.