При проведении исследований, разработке программного обеспечения и создании новых технологий, большое значение имеет оценка точности результатов. Погрешность, как неизбежное явление в любых измерениях и рассчетах, влияет на достоверность и надежность полученных данных. Определение цены погрешности является неотъемлемой частью научного и инженерного процесса.

Для того, чтобы эффективно оценить цену погрешности, необходимо применять определенные стратегии и методы. Первым шагом является выбор соответствующей метрики, которая будет использоваться для оценки точности. Это может быть абсолютная или относительная погрешность, среднеквадратичное отклонение или другие метрики, в зависимости от конкретной задачи.

Важным аспектом является также выбор соответствующего метода оценки погрешности. Среди самых распространенных методов можно выделить методы перекрестной проверки, бутстрэпа, анализа истинной погрешности и другие. Каждый из них имеет свои преимущества и ограничения, и выбор определенного метода зависит от поставленных задач и требований к точности исследования.

Что такое погрешность и как ее измерить

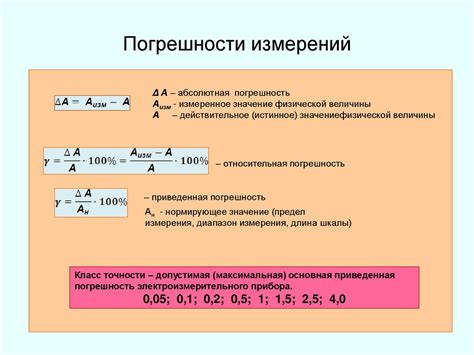
Измерение погрешности играет важную роль во многих областях, таких как физика, математика, инженерия, финансы и другие. Определение погрешности и ее измерение помогают оценить точность и достоверность полученных результатов и улучшить качество выполняемых расчётов и измерений.

Измерение погрешности может производиться с помощью различных методов и стратегий, в зависимости от прикладной области и характера измеряемых данных. Некоторые распространенные методы измерения погрешности включают использование статистических инструментов, математических моделей, компьютерных алгоритмов и симуляций.

Для измерения погрешности часто используются такие показатели, как средняя абсолютная погрешность (Mean Absolute Error), среднеквадратичная погрешность (Root Mean Square Error), относительная погрешность (Relative Error) и другие. Эти показатели позволяют оценить различные аспекты погрешности, такие как абсолютная величина ошибки, ее относительное значение или сравнение с другими измерениями или расчетами.

Важно отметить, что измерение погрешности не всегда является точным и окончательным. Иногда величина погрешности может быть определена только приближенно или статистически. Кроме того, необходимо учитывать и другие факторы, такие как систематическая ошибки или случайная природа измерений.

В итоге, измерение и оценка погрешности играют важную роль в научных и технических исследованиях, позволяя улучшить точность и достоверность результатов. Применение эффективных стратегий и методов измерения погрешности становится ключевым при решении различных задач и оптимизации процессов в различных областях деятельности.

Эффективные стратегии и методы определения цены погрешности

Существует несколько эффективных стратегий и методов, которые позволяют оценить цену погрешности с различными уровнями точности и достоверности.

Первая стратегия – аналитическое определение. Для простых расчетов существуют математические методы, позволяющие точно определить цену погрешности. Например, для линейных систем, можно использовать аналитические формулы, основанные на теории ошибок.

Однако, в большинстве случаев требуется применение численных методов для определения погрешности. Вторая стратегия – метод Монте-Карло. Этот метод основан на статистической обработке случайных чисел и репрезентативной выборке. Он применяется, когда аналитическое решение проблематично или невозможно. Метод Монте-Карло позволяет оценить цену погрешности с заданной точностью и уровнем доверия, проводя множество вычислений на случайно генерируемых данных.

Третья стратегия – методы с использованием аналитического решения и численных методов. В таких случаях, для оценки цены погрешности используют более эффективные и точные численные методы, основанные на приближенных аналитических решениях. Это позволяет сократить время вычислений, сохраняя достаточный уровень точности.

Каждая из этих стратегий имеет свои преимущества и ограничения, и выбор конкретного метода зависит от природы задачи, доступных ресурсов и требуемого уровня точности. Однако, независимо от выбранной стратегии, важно всегда учитывать все возможные исходные данные, риски и сделать достаточное количество повторных вычислений для получения устойчивых и надежных результатов.