Коэффициент детерминации является одним из наиболее распространенных и важных показателей в статистике. Он позволяет определить, насколько хорошо линейное уравнение регрессии описывает данные. В Excel существует специальная функция, которая позволяет вычислить этот показатель.
Для начала необходимо убедиться, что у вас есть два набора данных: независимые переменные (X) и зависимые переменные (Y). Убедитесь, что эти данные расположены в соответствующих столбцах или строках в таблице Excel.
Чтобы вычислить коэффициент детерминации, воспользуйтесь функцией R2. Введите следующую формулу в свободную ячейку: =R2 (диапазон_y, диапазон_x). Замените "диапазон_y" на диапазон зависимых переменных и "диапазон_x" на диапазон независимых переменных.
Excel автоматически вычислит и покажет коэффициент детерминации, который будет отображаться в общем формате числа с двумя десятичными знаками. Например, если коэффициент детерминации равен 0,75, это означает, что 75% вариации зависимых переменных может быть объяснено моделью регрессии.
Определение коэффициента детерминации в Excel
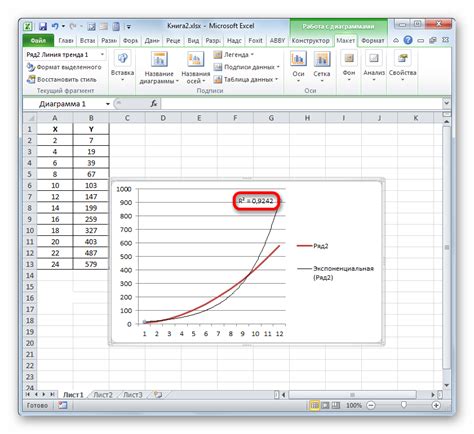
Для начала необходимо иметь две колонки данных: независимую переменную (X) и зависимую переменную (Y). Загрузите эти данные в два столбца листа Excel.
Затем выделите ячейку, в которую вы хотите поместить результат расчета коэффициента детерминации. Введите формулу R2, используя следующий синтаксис: =R2(диапазон_независимой_переменной, диапазон_зависимой_переменной).
Например, если данные находятся в столбцах A и B, формула будет выглядеть так: =R2(A1:A10, B1:B10).
После ввода формулы нажмите Enter, и Excel вычислит коэффициент детерминации для ваших данных.
Значение коэффициента детерминации будет варьироваться от 0 до 1. Чем ближе значение к 1, тем лучше модель объясняет вариацию в данных. Если значение коэффициента детерминации близко к 0, значит, модель плохо объясняет данные.
Теперь вы знаете, как определить коэффициент детерминации в Excel. Этот показатель поможет вам оценить качество модели и принять информированное решение на основе ваших данных.
Что такое коэффициент детерминации?

Коэффициент детерминации обозначается символом R² и может принимать значения от 0 до 1. Значение 0 означает, что ни одна из независимых переменных не объясняет вариацию зависимой переменной, а значение 1 указывает на то, что все вариации в зависимой переменной могут быть объяснены независимыми переменными.
Когда мы рассчитываем коэффициент детерминации в Excel, мы получаем численное значение, отражающее процент объясненной вариации. Это означает, что чем ближе значение R² к 1, тем лучше модель адекватно объясняет данные.
Однако следует отметить, что коэффициент детерминации не является единственной метрикой, по которой следует оценивать модель регрессии. Важно учитывать другие факторы, такие как стандартные ошибки регрессии, значимость коэффициентов и другие статистические тесты, чтобы получить полное представление о качестве модели.
Как рассчитать коэффициент детерминации в Excel?

Для начала, необходимо иметь два набора данных: массив значений независимой переменной (X) и массив соответствующих значений зависимой переменной (Y). В Excel эти данные могут быть расположены в двух столбцах.
Чтобы рассчитать коэффициент детерминации, выполните следующие шаги:
- Выберите ячейку, в которой будет отображаться результат.
- Введите формулу:
=RSQ(зависимая_переменная; независимая_переменная) - Нажмите "Enter".
Excel рассчитает коэффициент детерминации и отобразит его в выбранной ячейке. Значение коэффициента детерминации будет находиться в диапазоне от 0 до 1, где 0 означает, что модель не объясняет данные, а 1 - что модель идеально объясняет данные.
Коэффициент детерминации позволяет определить, какую долю вариации зависимой переменной объясняет модель. Более близкое к 1 значение указывает на более точную аппроксимацию данных.
Толкование значения коэффициента детерминации
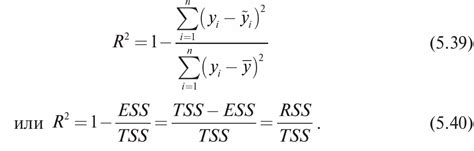
Значение коэффициента детерминации может варьироваться от 0 до 1. Значение 0 означает, что независимые переменные не объясняют зависимую переменную, а значение 1 означает, что все изменения в зависимой переменной полностью объясняются независимыми переменными.
Важно отметить, что значение коэффициента детерминации может быть даже отрицательным. Это может произойти, когда модель предсказывает значения зависимой переменной, которые отличаются от реальных значений в большую сторону.
Коэффициент детерминации также можно интерпретировать в процентном соотношении. Например, коэффициент детерминации 0,75 означает, что 75% изменчивости зависимой переменной объясняется независимыми переменными.
Важно помнить, что коэффициент детерминации не является конечной оценкой точности модели. Он лишь показывает, насколько хорошо модель согласуется с данными, но не дает информации о том, насколько точно модель сможет предсказывать новые данные.
| Значение коэффициента детерминации | Толкование |
|---|---|
| 0 | Независимые переменные не объясняют зависимую переменную |
| 0-0,5 | Независимые переменные слабо объясняют зависимую переменную |
| 0,5-0,75 | Независимые переменные умеренно объясняют зависимую переменную |
| 0,75-0,9 | Независимые переменные сильно объясняют зависимую переменную |
| 0,9-1 | Независимые переменные очень сильно объясняют зависимую переменную |
Применение коэффициента детерминации в анализе данных

Применение коэффициента детерминации в анализе данных является важным шагом для понимания взаимосвязей между переменными и предсказания будущих значений. Он позволяет определить, какая часть изменчивости в объясняемой переменной может быть объяснена независимыми переменными, а какая часть остается невыясненной.
Коэффициент детерминации обозначается R² и может принимать значения от 0 до 1. Значение 0 означает отсутствие связи между переменными, а значение 1 указывает на 100% объяснение изменчивости в объясняемой переменной. Чем ближе значение R² к 1, тем лучше модель соответствует данным и предсказывает значения объясняемой переменной.
Применение коэффициента детерминации в анализе данных позволяет не только оценить степень влияния независимых переменных на объясняемую переменную, но и сравнить различные модели между собой. Более высокое значение R² указывает на более точную и предсказуемую модель.
Использование коэффициента детерминации помогает исследователям и аналитикам принимать обоснованные решения на основе анализа данных. Он дает возможность понять, насколько успешно модель объясняет изменчивость в данных и может быть использован для прогнозирования будущих значений.