Компонента связности графа - это группа вершин, где каждая из них можно достичь из любой другой вершины, используя ребра графа. Определение количества компонент связности графа - важная задача в анализе сетей и социальных графов. Python предоставляет удобные инструменты для решения этой задачи.
Для определения количества компонент связности графа в Python можно использовать алгоритм обхода в глубину (Depth-First Search, DFS). Этот алгоритм позволяет посетить все вершины, достижимые из заданной вершины. После обхода графа DFS можно посчитать количество компонент связности, считая количество вызовов алгоритма.
Python предоставляет также библиотеку NetworkX, которая содержит множество функций для работы с графами. Используя NetworkX, можно очень легко определить количество компонент связности графа. Библиотека также предоставляет возможность визуализации графов и проведения сложных анализов.
Итак, в этой статье мы рассмотрим два метода определения количества компонент связности графа в Python: с помощью алгоритма обхода в глубину и с использованием библиотеки NetworkX. Оба метода довольно просты и пригодны для использования в большинстве задач анализа графов.
Что такое граф в программировании?

В графе каждая вершина представляет собой отдельный объект или элемент данных, а ребра представляют собой отношения или связи между этими объектами. Ребра могут быть направленными или нет, что определяет, можно ли переходить от одной вершины к другой только в одном направлении или в обоих направлениях.
| Термин | Описание |
|---|---|
| Вершина | Элемент данных или объект, представленный в графе |
| Ребро | Связь между двумя вершинами в графе |
| Направленный граф | Граф, в котором ребра имеют определенное направление |
| Ненаправленный граф | Граф, в котором ребра не имеют определенного направления |
| Смежные вершины | Вершины, которые имеют общее ребро |
| Компонент связности | Максимальная связная подграф, в котором есть связь между любой парой вершин |
Графы широко используются в программировании для решения различных задач и алгоритмов, связанных с поиском путей, оптимизацией сетей, анализом социальных связей и многими другими областями. Для работы с графами в программировании существуют различные алгоритмы и структуры данных, которые позволяют эффективно оперировать графами и решать задачи, связанные с ними.
Определение графа
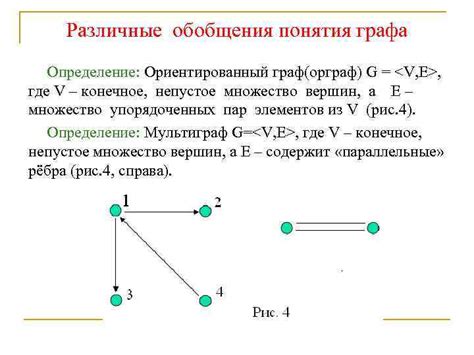
Вершины - это отдельные элементы графа, которые могут быть представлены как точки или узлы. Каждая вершина может иметь свое название или метку.
Ребра - это связи между вершинами. Ребра могут быть направленными или ненаправленными. Если ребро имеет направление от одной вершины к другой, то говорят о направленном графе. Если ребра не имеют направления, то говорят о ненаправленном графе.
Графы широко используются в различных областях, таких как информатика, математика, транспортная логистика, социальные сети и т.д. Их структура и связи между элементами дают возможность анализировать и решать различные задачи.
Компоненты связности графа: понятие и примеры
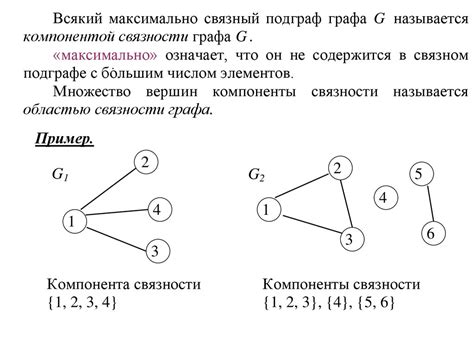
Компонента связности состоит из максимального множества вершин графа, в котором каждая вершина связана с каждой другой вершиной путем некоторого пути. Между вершинами одной компоненты связности можно проложить путь, а между вершинами разных компонент пути нет.
Примером компонент связности может служить социальная сеть. Представим себе граф, в котором вершины – это пользователи, а ребра – дружественные связи между ними. Каждая компонента связности представляет отдельное сообщество: группу друзей, имеющих между собой связи. Внутри каждой компоненты связности существуют пути, по которым можно перейти от одного пользователя к другому, но между компонентами связности пути отсутствуют.
Как определить количество компонент связности в графе?

Алгоритм обхода в глубину состоит из следующих шагов:
- Выбрать стартовую вершину и пометить ее как посещенную.
- Получить список смежных вершин и рекурсивно вызвать алгоритм для каждой непосещенной смежной вершины.
- Повторять шаг 2 для каждой непосещенной вершины до тех пор, пока все вершины не будут посещены.
- Количество вызовов алгоритма будет равно количеству компонент связности в графе.
Алгоритм обхода в ширину работает похожим образом, но использует очередь вместо стека для определения порядка обхода вершин.
Эти алгоритмы могут быть реализованы с использованием языка программирования Python. Для этого можно воспользоваться готовыми библиотеками, такими как NetworkX, которая предоставляет инструменты для работы с графами.
Программирование графов в Python: библиотеки и алгоритмы

Одной из наиболее популярных библиотек для работы с графами является NetworkX. Она предоставляет широкий набор функций и алгоритмов для создания, модификации и анализа графов. С помощью NetworkX можно строить графы, добавлять и удалять вершины и ребра, а также выполнять различные операции с графами, такие как поиск кратчайших путей, определение количества компонент связности и многое другое.
Еще одной из популярных библиотек для работы с графами в Python является igraph. Она предоставляет эффективные структуры данных и алгоритмы для работы с графами больших размеров. igraph позволяет создавать, модифицировать и анализировать графы, а также выполнять различные операции над ними, такие как нахождение центральности вершин, определение сообществ в сети и многое другое.
В Python также представлены и другие библиотеки для работы с графами, такие как graph-tool, SNAP и др. Они предоставляют различные функциональные возможности и алгоритмы для работы с графами, в зависимости от потребностей пользователя.
Помимо библиотек, в Python существуют различные алгоритмы для работы с графами. Некоторые из них включены в состав библиотек, например, алгоритм Косарайю для определения компонент связности. Другие алгоритмы можно реализовать самостоятельно, используя базовые структуры данных и операции. Например, алгоритмы поиска в глубину и ширину позволяют определить компоненты связности, находить кратчайшие пути и выполнять другие операции над графами.
Таким образом, программирование графов в Python предоставляет широкий набор инструментов для работы с графами различной сложности. Библиотеки и алгоритмы позволяют создавать, модифицировать и анализировать графы, а также выполнять различные операции над ними. Это делает Python удобным и мощным инструментом для работы с графами в анализе данных и других областях.