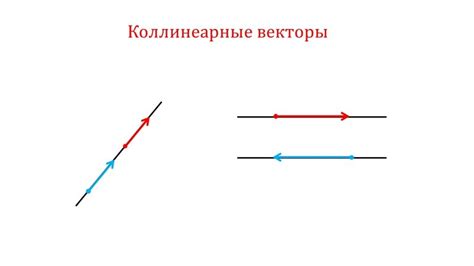
Коллинеарность - это свойство, определяющее, являются ли два вектора параллельными и находятся ли они на одной прямой. Когда векторы коллинеарны, они имеют одинаковое направление и могут отличаться только по длине.
Для определения коллинеарности векторов, мы можем использовать их координаты. Координаты вектора - это числа, которые определяют положение вектора в пространстве. Координаты записываются в виде упорядоченной последовательности чисел, где каждое число соответствует компоненте вектора по определенной оси.
Если у двух векторов все соответствующие координаты пропорциональны друг другу, то эти векторы коллинеарны. Другими словами, если для векторов A и B выполняется условие:
A = k * B,
где k - постоянное значение, то векторы A и B коллинеарны. Таким образом, мы можем определить коллинеарность векторов, сравнивая их координаты и ища соотношение пропорциональности.
Что такое коллинеарность векторов?
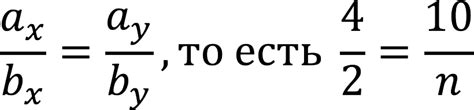
Коллинеарность векторов играет важную роль во многих областях математики и физики. Она может быть использована для определения параллельности линий, решения систем линейных уравнений и нахождения базиса линейного пространства. Коллинеарность векторов также часто используется для решения геометрических задач, таких как нахождение середины отрезка или определение пересечения прямых.
Если векторы a и b коллинеарны, их можно записать в виде a = k * b, где k - произвольное число. Также векторы a и b коллинеарны, если и только если их координаты удовлетворяют однородному системе уравнений.
Таким образом, знание о коллинеарности векторов позволяет нам лучше понимать и анализировать связи между векторами и использовать их в различных математических и физических приложениях.
Определение коллинеарности векторов в геометрии
Для определения коллинеарности векторов используются различные методы, основанные на свойствах векторов. Один из таких методов - сравнение координат векторов.
Координаты вектора могут быть представлены числами или переменными, соответствующими составляющим вектора по каждой из осей координат. Для двух векторов A и B коллинеарность можно определить, сравнивая их координаты.
Если все координаты вектора B пропорциональны координатам вектора A с соответствующим коэффициентом пропорциональности k, то векторы A и B коллинеарны. Математически это можно записать следующим образом:
B = kA, где k - коэффициент пропорциональности.
Таким образом, коллинеарность векторов возможно определить путем проверки соотношения между их координатами. Если это соотношение существует, то векторы коллинеарны, то есть лежат на одной прямой или параллельны друг другу.
Различные методы определения коллинеарности векторов позволяют решать разнообразные геометрические задачи, связанные с построением и анализом фигур.
Физическое определение коллинеарности векторов

Физическое определение коллинеарности векторов можно проиллюстрировать на примере движения автомобиля. Если два автомобиля движутся по одной прямой дороге в одном направлении с одинаковой скоростью, их векторы скорости будут коллинеарными. В этом случае, можно сказать, что эти автомобили движутся параллельно друг другу, так как их векторы скорости направлены вдоль одной и той же линии.
Еще одним примером является движение двух объектов на плоскости. Если два объекта движутся по прямым линиям, их векторы перемещения будут коллинеарными. Таким образом, можно сказать, что эти объекты движутся вдоль одной и той же линии, в одном направлении или в противоположных направлениях.
Физическое определение коллинеарности векторов отражает их взаимное расположение в физическом пространстве и помогает нам понять, как они взаимодействуют друг с другом в конкретных ситуациях.
Математическое понятие коллинеарности векторов

Для определения коллинеарности векторов используются геометрические и алгебраические методы. Геометрический метод основывается на сравнении направлений и длин векторов. Если векторы имеют одно направление и могут быть записаны как кратные друг другу, то они являются коллинеарными.
Алгебраический метод основывается на анализе линейной комбинации векторов. Два или более векторов считаются коллинеарными, если они могут быть выражены через общий множитель. Например, если векторы A и B являются коллинеарными, то они могут быть выражены как A = k * B, где k – общий множитель.
Для более точного определения коллинеарности векторов можно использовать таблицу, в которой векторы представлены в виде их компонентов или координат. Если координаты векторов могут быть выражены как пропорции или общие кратные, то векторы считаются коллинеарными.
| Вектор | Координаты |
|---|---|
| A | (x1, y1, z1) |
| B | (x2, y2, z2) |
| C | (x3, y3, z3) |
Если векторы A, B и C коллинеарны, то можно заметить, что отношения между координатами равны. Например, отношение x1 / x2 = y1 / y2 = z1 / z2, x1 / x3 = y1 / y3 = z1 / z3 и т.д.
В практических применениях коллинеарность векторов имеет множество применений, например, в физике, геометрии, компьютерной графике и других областях. Понимание коллинеарности позволяет анализировать направления и связи между векторами в пространстве.
Как распознать коллинеарность векторов?
Существуют различные способы определения коллинеарности векторов:
| 1. Графический метод: | Построение векторов на плоскости и проверка, лежат ли они на одной прямой или параллельны друг другу. |
| 2. Алгебраический метод: | Вычисление векторного произведения векторов. Если векторное произведение равно нулю, то векторы коллинеарны. |
| 3. Координатный метод: | Проверка соотношений между координатами векторов. Если координаты векторов пропорциональны, то они коллинеарны. |
Важно отметить, что нулевой вектор всегда коллинеарен с любым другим вектором, так как он имеет нулевую длину и не имеет определенного направления.
Распознавание коллинеарности векторов является важным понятием в линейной алгебре и находит применение во многих областях, таких как физика, геометрия и компьютерная графика.
Значение коллинеарности векторов в приложениях
Одним из наиболее распространенных применений коллинеарности векторов является расчет угла между ними. Если два вектора коллинеарны (то есть лежат на одной прямой), то угол между ними равен 0 градусов. Если же векторы не коллинеарны, то угол может быть разным и используется формула для его вычисления.
Коллинеарность векторов также применяется в компьютерной графике для определения направления освещения объектов. Например, если основной источник света находится в точке А, а вектор нормали к поверхности объекта указывает в направлении от точки В к точке С, то можно определить интенсивность освещения в данной точке, с учетом угла между вектором нормали и вектором от точки В к точке А.
Определение коллинеарности векторов имеет также важное значение в геометрии. Например, при решении задач на принадлежность точки отрезку, необходимо определить, лежит ли вектор, отображающий отрезок, на одной прямой с векторами, отображающими начальную и конечную точки отрезка. Если векторы коллинеарны, то можно утверждать, что точка принадлежит отрезку.
Таким образом, коллинеарность векторов имеет широкое применение в различных областях науки и техники, где важно определить взаимные отношения и расположение объектов, а также углы между ними.
Геометрическое свойство коллинеарности векторов
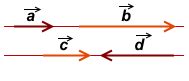
Определение коллинеарности векторов проводится путем сравнения направлений векторов. Если два вектора имеют одинаковые или противоположные направления, то они считаются коллинеарными. Направление вектора определяется углом, который он образует с положительным направлением оси координат.
Если векторы коллинеарны, то между ними существует линейная зависимость. Это означает, что один вектор может выразиться через другой с помощью умножения на константу. Например, для векторов a и b их коллинеарность можно выразить уравнением a = kb, где k - константа.
Коллинеарность векторов имеет важное значение в геометрии и физике. Например, векторы, описывающие силы в механике, обладают коллинеарностью при параллельном направлении или противоположной ориентации.
Коллинеарность векторов часто используется для решения геометрических задач. Например, для определения равенства длин векторов можно проверить их коллинеарность и равенство направлений.
Физические примеры коллинеарности векторов

Один из примеров коллинеарности векторов в физике - это движение тела по прямой линии под действием постоянной силы. В этом случае сила и ускорение, которое она создает, направлены вдоль одной прямой, их векторы коллинеарны.
Еще один пример - это электромагнитное поле, создаваемое прямолинейным проводником с постоянным током. Магнитное поле и направление тока также коллинеарны.
Другой физический пример - это световые волны. Векторы электрического и магнитного полей света коллинеарны и перпендикулярны направлению распространения волны.
В механике коллинеарность часто возникает при рассмотрении движения по прямой и кратчайших путей. Например, при решении задач о движении тела по наклонной плоскости коллинеарность векторов силы гравитации и нормальной реакции должна быть учтена.
Коллинеарность векторов имеет большое значение в физических и инженерных расчетах. Она позволяет упростить анализ системы и делает математические модели более понятными и удобными для работы.
| Пример | Векторы |
|---|---|
| Движение тела по прямой | Сила, ускорение |
| Провод с постоянным током | Магнитное поле, направление тока |
| Световые волны | Электрическое поле, магнитное поле |
| Движение по наклонной плоскости | Сила гравитации, нормальная реакция |
Математические примеры коллинеарности векторов

Рассмотрим несколько примеров, чтобы лучше понять этот концепт:
Пример 1:
Пусть у нас есть два вектора:
- Вектор A = (2, 4)
- Вектор B = (4, 8)
Для того чтобы проверить, являются ли эти векторы коллинеарными, нужно сравнить их координаты.
В данном случае можно заметить, что вектор B получается умножением вектора A на 2:
Вектор B = 2 * Вектор A
Таким образом, векторы A и B являются коллинеарными.
Пример 2:
Рассмотрим следующие векторы:
- Вектор C = (3, 6)
- Вектор D = (-1, -2)
Если умножить вектор C на -2, получим вектор D:
Вектор D = -2 * Вектор C
Также можем заметить, что если умножить вектор D на -1/2, получим вектор C:
Вектор C = -1/2 * Вектор D
Значит, векторы C и D являются коллинеарными.
Таким образом, векторы являются коллинеарными, если один получается путем умножения другого на константу.
Преимущества и недостатки коллинеарности векторов

Преимущества коллинеарности векторов:
- Простота анализа. Коллинеарные векторы легко анализировать, так как они имеют одинаковое направление или противоположное направление. Это позволяет свести сложные геометрические задачи к более простым.
- Упрощение вычислений. Когда векторы коллинеарны, операции с ними упрощаются. Например, сложение или вычитание коллинеарных векторов сводится к сложению или вычитанию их модулей.
- Удобство визуализации. Когда векторы коллинеарны, их можно представить на графике как отрезки на одной прямой, что упрощает их визуализацию и понимание связей между ними.
Недостатки коллинеарности векторов:
- Ограниченная информация. Коллинеарные векторы не дают полной информации о форме объекта или системы. Они могут быть полезны только для описания линейных связей и направлений.
- Сокращение размерности. Когда векторы коллинеарны, размерность системы может быть сокращена. Это может быть нежелательным, если необходимо учитывать все аспекты системы.
- Чувствительность к погрешностям. В случае небольших отклонений от коллинеарности, результаты расчетов и анализа могут сильно отличаться, что делает эту характеристику нестабильной.
Как использовать коллинеарность векторов в своих расчетах?

Использование коллинеарности векторов позволяет упростить множество математических расчетов и облегчить понимание геометрических свойств объектов. Вот некоторые способы применения коллинеарности векторов в своих расчетах:
| 1. Поиск кратчайшего пути |
|---|
| В некоторых задачах, например, при нахождении кратчайшего пути между двумя точками на плоскости, можно использовать коллинеарность векторов для оптимизации алгоритма. Если известно, что векторы, соединяющие точки, коллинеарны, то можно сократить количество вычислений и ускорить процесс нахождения кратчайшего пути. |
| 2. Проверка линейной зависимости |
| Коллинеарность векторов также помогает определить линейную зависимость между векторами. Если два или более вектора коллинеарны, то они линейно зависимы. Это может быть полезно при решении систем линейных уравнений или анализе множества векторов. |
| 3. Геометрические преобразования |
| Коллинеарность векторов применяется при выполнении геометрических преобразований, таких как поворот, масштабирование и отражение объектов. Зная, что векторы коллинеарны, можно легко изменить размер или направление объекта без необходимости выполнять сложные вычисления. |