Определение наибольшего общего делителя и наименьшего общего кратного чисел в Python — примеры и объяснения

В программировании часто возникают задачи, связанные с нахождением наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух или большего количества чисел. НОД - это наибольшее число, которое делит все заданные числа без остатка, а НОК - это наименьшее число, которое делится на все заданные числа без остатка.

В Python существует несколько способов решения этих задач. Один из самых простых способов - использование встроенной функции gcd() из модуля math для нахождения НОД.

Для нахождения НОК можно воспользоваться формулой: НОК(a, b) = (a * b) / НОД(a, b). Также можно использовать цикл while для поиска НОК двух чисел.

В данной статье мы рассмотрим несколько примеров кода для нахождения НОД и НОК чисел в Python, а также объясним, как они работают.

Определение наибольшего общего делителя

Для определения НОД существуют несколько методов, один из которых основан на поиске общих делителей чисел. Один из эффективных методов - это алгоритм Евклида.

Алгоритм Евклида заключается в последовательном делении двух чисел и нахождении остатка от деления. Итеративно повторяя эту операцию, можно найти НОД чисел. Когда остаток от деления становится равным нулю, предыдущее число делит нацело следующее число, а следующее число становится НОД.

Например, для чисел 54 и 24:

• 54 / 24 = 2 (остаток 6)
• 24 / 6 = 4 (остаток 0)

Таким образом, НОД чисел 54 и 24 равен 6.

Алгоритм Евклида является легким и эффективным способом нахождения НОД чисел в Python. Он может быть реализован как в виде итерационной функции с помощью цикла, так и в виде рекурсивной функции.

Наименьшее общее кратное чисел

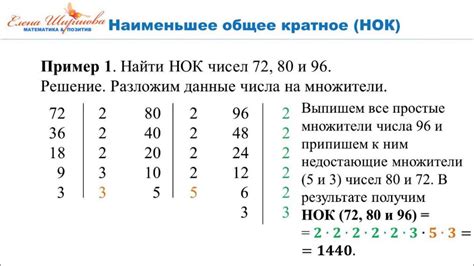
Для нахождения НОК двух чисел можно использовать формулу:

1. Найдите наибольший общий делитель (НОД) чисел, используя алгоритм Евклида или другой подход.
2. Умножьте числа, разделив их на НОД, и поделите полученное произведение на НОД. Это и будет НОК этих чисел.

Например, найдем НОК чисел 12 и 18:

1. Найдем НОД чисел 12 и 18, используя алгоритм Евклида:

• 18 % 12 = 6
• 12 % 6 = 0

• (12 * 18) / 6 = 36

Таким образом, НОК чисел 12 и 18 равен 36.

Алгоритм можно распространить на нахождение НОК более чем двух чисел. Для этого необходимо последовательно находить НОК пар чисел с помощью указанной выше формулы и затем использовать полученные значения для нахождения НОК следующих пар чисел.

Примеры нахождения наибольшего общего делителя и наименьшего общего кратного в Python

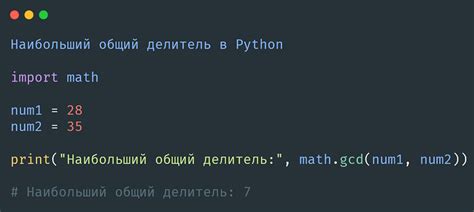
Метод 1: Использование встроенной функции math.gcd()

import math
a = 12
b = 18
gcd = math.gcd(a, b)
lcm = abs(a*b) // gcd
print(f"НОД чисел {a} и {b}: {gcd}")
print(f"НОК чисел {a} и {b}: {lcm}")

В этом примере мы используем встроенную функцию math.gcd() из модуля math для нахождения НОД чисел. Затем мы находим НОК, используя формулу НОК = |a * b| / НОД.

Метод 2: Использование алгоритма Евклида

def gcd_euclidean(a, b):
while b != 0:
a, b = b, a % b
return a
def lcm(a, b):
return abs(a*b) // gcd_euclidean(a, b)
a = 12
b = 18
gcd = gcd_euclidean(a, b)
lcm = lcm(a, b)
print(f"НОД чисел {a} и {b}: {gcd}")
print(f"НОК чисел {a} и {b}: {lcm}")

В этом примере мы определяем две функции: gcd_euclidean() для вычисления НОД с помощью алгоритма Евклида и lcm() для нахождения НОК с использованием формулы НОК = |a * b| / НОД. Затем мы вызываем эти функции и печатаем результаты.

Обратите внимание, что в обоих примерах мы используем функцию abs() для обработки отрицательных чисел и // для выполнения целочисленного деления.

Объяснения алгоритмов нахождения наибольшего общего делителя и наименьшего общего кратного

Существуют различные алгоритмы для нахождения НОД и НОК чисел, но два из них являются основными и широко используются.

Алгоритм Евклида для нахождения НОД:

1. Для начала выбираются два числа, для которых нужно найти НОД.
2. Производится деление большего числа на меньшее.
3. Полученный остаток становится новым меньшим числом, а предыдущее меньшее число - новым большим числом.
4. Шаги 2-3 повторяются до тех пор, пока полученный остаток не станет равным нулю.
5. Когда остаток становится равным нулю, последнее меньшее число (не равное нулю) является НОД исходных чисел.

Алгоритм нахождения НОК с использованием НОД:

1. Для начала выбираются два числа, для которых нужно найти НОК.
2. Находится НОД этих двух чисел с использованием алгоритма Евклида.
3. НОК вычисляется по формуле: НОК = (произведение исходных чисел) / НОД.

Эти алгоритмы являются эффективными и широко используются как в математике, так и в программировании. Они позволяют находить НОД и НОК чисел быстро и надежно.