Определение области функции является важным этапом при изучении математики и анализа. Область функции - это множество всех возможных значений, которые может принимать функция. Понимание области функции позволяет определить, в каких пределах можно использовать функцию и какие значения она может принимать.
Существует несколько способов определения области функции. Первый и наиболее простой способ - это анализ выражения функции. Заключается он в исследовании различных ограничений, которые могут присутствовать в выражении функции. Например, если функция содержит знаменатель, то необходимо исключить значения, при которых знаменатель обращается в ноль.
Другой способ определения области функции - это графический анализ. График функции позволяет визуально оценить, какие значения принимает функция на всем допустимом интервале. Если график функции ограничен в определенном диапазоне, то и область функции будет ограничена в этом же диапазоне.
Понимание области функции является важным навыком при решении математических задач и построении моделей. Оно позволяет определить, какие значения можно использовать при работе с функцией и прогнозировать ее поведение в определенных условиях. Практика решения задач, анализ графиков и использование математических инструментов помогут развить этот навык и сделать определение области функции более точным и эффективным.
Что такое область функции?

Для того чтобы определить область функции, необходимо учитывать такие факторы, как:
- Значения, которые можно подставить в функцию без нарушения ее определения. Например, функция sqrt(x) определена только для неотрицательных значений, поэтому ее областью будет множество неотрицательных чисел.
- Значения, которые в результате выполнения функции могут привести к неопределенности или недопустимым математическим операциям. Например, функция 1/(x-2) не определена при x=2, поэтому в область функции не входит значение 2.
- Условия, накладываемые на аргументы функции. Например, функция log(x) определена только для положительных значений аргумента x, поэтому ее областью будет интервал (0, +∞).
Знание области функции важно при решении уравнений, определении максимума или минимума функции, анализе ее поведения, а также во многих других математических задачах. Поэтому при изучении функций важно уметь определять и анализировать их область.
Определение и примеры

Чтобы определить область функции, необходимо рассмотреть все ограничения и ограничения функции. Это включает в себя:
- Деление на ноль: Функция может быть не определена при делении на ноль. Например, функция f(x) = 1/x не определена при x = 0. Следовательно, область этой функции - все значения x, кроме 0.
- Квадратный корень: Функция с квадратным корнем не определена, если подкоренное выражение отрицательное. Например, функция g(x) = √(x - 4) не определена, если x - 4 < 0. Следовательно, область этой функции - все значения x, которые больше или равны 4.
- Логарифм: Функция логарифма не определена для отрицательных или нулевых аргументов. Например, функция h(x) = ln(x) не определена для x ≤ 0. Следовательно, область этой функции - все значения x, которые больше 0.
Вот несколько примеров, чтобы прояснить понятие области функции:
- Пример 1: Рассмотрим функцию f(x) = 3x + 2. В этом случае область функции - все значения x, которые являются действительными числами.
- Пример 2: Рассмотрим функцию g(x) = √(x - 4). В этом случае область функции - все значения x, которые больше или равны 4.
- Пример 3: Рассмотрим функцию h(x) = 1/(x - 2). В этом случае область функции - все значения x, кроме 2.
Таким образом, определение области функции и рассмотрение всех ограничений помогают точно определить, для каких значений функция определена и имеет смысл.
Графическое представление области функции
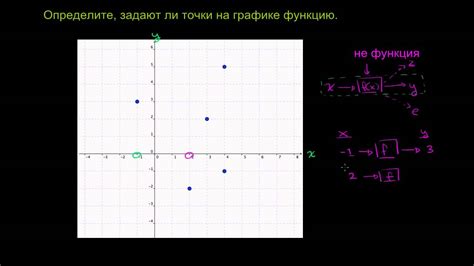
Пусть дана функция f(x) = √(4 - x^2). Чтобы определить её область определения, можно построить её график. Для этого необходимо нарисовать оси координат и отметить точки, которые принадлежат графику функции. Затем найти все значения x, при которых функция имеет смысл. В данном случае, функция определена только при x ∈ [-2, 2], так как при значениях x < -2, x > 2 функция не имеет смысла из-за отрицательного значения под корнем.
Другой пример: функция g(x) = 1/(x - 2). Чтобы определить её область определения, нужно найти все значения x, при которых функция определена. В данном случае, функция будет неопределена при x = 2, так как при таком значении в знаменателе будет ноль. Таким образом, область определения функции g(x) - все значения x, кроме x = 2.
Графическое представление области функции помогает наглядно определить, при каких значениях переменной функция имеет смысл. Это очень полезный инструмент при работе с функциями, особенно сложными и составными.
Как определить область функции?

Шаги для определения области функции:
- Изучите выражение функции и определите все ограничения, наложенные на входные значения посредством арифметических операций, корней, логарифмов, деления на ноль и т.д. Возможные ограничения включают отрицательные значеня под корнем, деление на ноль и домены логарифмов.
- Проанализируйте ограничения и определите, какие значения могут быть входными значениями функции, чтобы она оставалась определенной и имела смысл. Не забудьте учитывать как числовые ограничения, так и домены функций, таких как квадратные корни и логарифмы, которые могут иметь только определенные входные значения.
- Запишите область функции в математической нотации, используя неравенства, интервалы или комбинации обоих. Например, если функция имеет ограничение на входные значения x > 0 и x < 10, то область функции можно записать как (0, 10).
Пример:
Рассмотрим функцию f(x) = 1 / x, где x - входное значение функции.
Ограничения: x не может быть равно нулю.
Значит, область функции будет записана как x ≠ 0 (x не равно нулю).
Таким образом, область функции f(x) = 1 / x - все значения x, кроме нуля.
Применение области функции в реальной жизни

- Бизнес и экономика: Предпринимателям важно определить область функции, чтобы понять, в каком диапазоне значений их бизнес будет успешным. Например, при анализе продаж товаров нужно знать, при каких ценах и объемах продаж предприятие будет получать прибыль.
- Физика: В физике область функции может использоваться для определения различных физических величин. Например, при изучении движения тела, функция может показывать зависимость пути от времени, и область функции определит допустимые значения времени и пути.
- Информационные технологии: При разработке программ и алгоритмов, определение области функции помогает избежать ошибок и некорректного использования входных данных. Функция может иметь ограничения на тип данных или на диапазон значений.
- Медицина: В медицине область функции может использоваться для анализа и классификации здоровья пациентов. Например, при оценке показателей кровяного давления, область функции может показывать нормальные значения и предупреждать о возможных проблемах.
- Строительство: При проектировании зданий и сооружений, область функции используется для определения допустимых нагрузок на конструкции. Функция может определять, какая нагрузка будет безопасной и не приведет к поломке или разрушению.
Это всего лишь несколько примеров из множества сфер, где понимание области функции является важным и полезным. Знание области функции помогает принимать верные решения, избегать ошибок и получать нужные результаты в различных областях жизни.