Определение области определения функции является одной из важных задач математики. Для функций, содержащих логарифмы и корни, эта задача может быть особенно запутанной и требовать тщательного анализа.
Логарифм и корень - это математические операции, которые используются для решения различных задач и вычислений. Однако, не все значения аргумента могут быть подставлены в функцию с логарифмом или корнем, так как в таких случаях может произойти деление на ноль или возникнуть отрицательное значение под корнем.
Для определения области определения функции с логарифмом необходимо рассмотреть два случая. В первом случае, если логарифм имеет основание больше единицы, то аргумент функции должен быть строго положительным числом. Во втором случае, в функции с логарифмом с основанием меньше единицы, аргумент должен быть строго отрицательным числом.
Для функций с корнем определение области определения может быть более сложным. Корень любой четной степени из отрицательного числа будет иметь комплексные корни, поэтому аргумент функции должен быть неотрицательным числом. Однако, корень нечетной степени может быть извлечен из отрицательных чисел, поэтому в этом случае аргумент функции может быть любым действительным числом.
Определение области определения функции
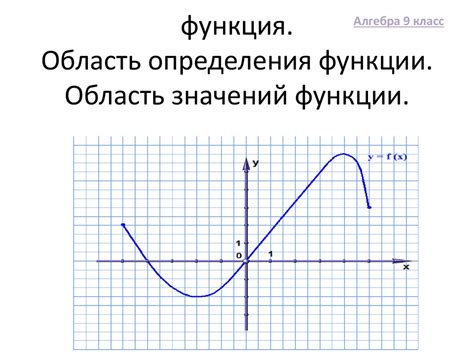
Для функций с логарифмом область определения определяется ограничениями, накладываемыми на аргументы. Логарифм с основанием a от x определен только для положительных значений x, поэтому его область определения будет множество всех значений x, больших нуля.
Аргументы функций с корнем должны быть неотрицательными числами, поэтому область определения таких функций будет множество всех значений x, больших или равных нулю.
Для функций, содержащих и логарифм, и корень, необходимо учитывать оба ограничения на аргументы. Таким образом, область определения таких функций будет множество всех положительных значений x, больших нуля.
Правильное определение области определения функции важно, так как оно позволяет избежать ошибок при вычислении функции и использовании ее значений в дальнейших вычислениях.
Определение логарифма

Логарифм обозначается как logab, и представляет собой показатель степени, в которую нужно возвести основание a, чтобы получить число b. Иными словами, logab = x, если a^x = b.
Основание логарифма может быть любым положительным числом, кроме 1. Наиболее часто используемыми основаниями являются 10 (десятичный логарифм) и e (натуральный логарифм).
Логарифмы широко применяются в различных областях науки, техники и экономики. Они позволяют преобразовывать сложные арифметические операции в простые логарифмические операции, упрощая расчеты и уменьшая сложность вычислений.
Свойства логарифма

| Свойство | Формула | Описание |
|---|---|---|
| Логарифм от произведения | \(\log(ab) = \log(a) + \log(b)\) | Логарифм произведения двух чисел равен сумме логарифмов этих чисел. |
| Логарифм от частного | \(\log\left(\frac{a}{b} ight) = \log(a) - \log(b)\) | Логарифм частного двух чисел равен разности логарифмов этих чисел. |
| Логарифм от степени | \(\log(a^n) = n\log(a)\) | Логарифм числа, возведенного в степень, равен произведению этой степени на логарифм числа. |
| Логарифм от единицы | \(\log(1) = 0\) | Логарифм единицы равен нулю. |
Эти свойства позволяют упростить вычисления с логарифмами и преобразовывать сложные выражения.
Определение корня
Определение корня функции является важным шагом в анализе функций и их графиков. Если мы знаем корни функции, то мы можем определить, где график функции пересекает ось x.
Если функция имеет несколько корней, они могут быть двойными или более. Количественно корни можно определить с помощью аналитических методов или методов численного решения уравнения f(x) = 0.
Не все функции имеют корни. Например, функция f(x) = x2 + 1 не обращается в ноль ни при каком значении x. В этом случае можно сказать, что функция не имеет корней.
Определение корня функции позволяет нам найти точки, в которых функция меняет знак. Это важно для определения интервалов, где функция возрастает и убывает, что дает нам полезную информацию о поведении функции.
Свойства корня

Свойства корня позволяют упростить вычисления и решать сложные задачи. Вот основные свойства корней:
- Существование и единственность корня. Для положительного радиканда всегда существует единственное положительное число, которое возводится в данную степень и равняется радиканду. Если радиканд равен нулю, то корнем будет ноль. Если радиканд отрицательный, то корня не существует в множестве действительных чисел.
- Свойство дистрибутивности. Когда корень умножается на число или складывается с другим корнем, можно вынести корень за скобки или объединить корни в один.
- Свойство степени. Корень можно возводить в степень, а также возводить число в степень корня.
- Свойство отвержения. Если радиканд отрицательный, то корень не существует в множестве действительных чисел.
- Свойство эквивалентности. Если корни равны, то и радиканды этих корней также равны.
Знание и понимание этих свойств позволяет упростить вычисления с корнями и применять их в различных задачах, связанных с математикой, физикой, экономикой и другими областями науки и техники.
Область определения функции с логарифмом

Для определения области определения функции с логарифмом необходимо учесть два условия:
1. Аргумент логарифма должен быть строго положительным числом, то есть:
x > 0
2. Выражение под знаком логарифма должно быть отлично от нуля, а именно:
y ≠ 0
Таким образом, область определения функции с логарифмом будет задаваться следующим неравенством:
x > 0 и y ≠ 0
В этой области значения функции с логарифмом определены и могут быть вычислены. За пределами этой области функция не определена.
Область определения функции с корнем
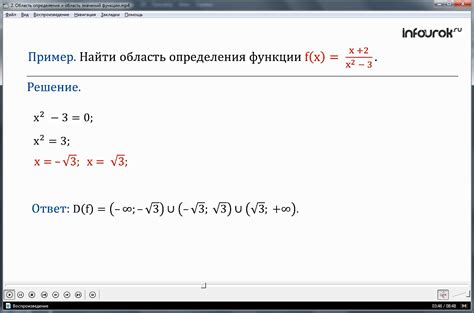
Для определения области определения функции с корнем необходимо обратить внимание на знак выражения под корнем. В силу свойства корня из отрицательного числа неизвестная функция определена только при выполнении особых условий.
Рассмотрим функцию вида:
f(x) = √(g(x)),
где g(x) - выражение под корнем.
Для определения области определения функции с корнем, нужно найти условия, при которых подкоренное выражение g(x) положительное или нулевое, так как корень из отрицательных чисел является мнимым числом и не имеет смысла в рамках вещественной арифметики.
Область определения функции можно представить в виде таблицы:
| Область определения f(x) = √(g(x)) |
|---|
| Если g(x) ≥ 0 |
| Если g(x) ≠ 0 |
То есть, для области определения функции с корнем, значение функции определено только при условии, что выражение под корнем неотрицательное и не равно нулю. В остальных случаях функция не определена.
Примеры:
1) Рассмотрим функцию f(x) = √(x). В данном случае выражение под корнем должно быть неотрицательным, то есть x ≥ 0.
Таким образом, область определения функции f(x) = √(x) - это все неотрицательные числа или интервал [0, +∞).
2) Рассмотрим функцию f(x) = √(x - 2). Здесь выражение под корнем должно быть неотрицательным, то есть x - 2 ≥ 0. Решаем неравенство:
x - 2 ≥ 0
x ≥ 2
Таким образом, область определения функции f(x) = √(x - 2) - это все числа, которые больше или равны 2, или интервал [2, +∞).