Область значений математической функции - это множество всех возможных значений, которые функция может принимать. Понимание области значений является важной частью изучения функций и позволяет нам понять, какие значения функции являются допустимыми и в каких промежутках они находятся.
Чтобы определить область значений функции, мы анализируем ее выражение и ограничения, которые могут быть наложены на переменные. В некоторых случаях область значений может быть очевидна, например, для линейной функции область значений будет всей числовой прямой. Однако, в более сложных случаях, требуется более тщательный анализ.
Одной из наиболее полезных техник для определения области значений является анализ поведения функции при приближении аргументов к бесконечности. Если функция имеет верхние или нижние границы при приближении аргументов к бесконечности, то эти границы могут ограничивать область значений функции.
Например, рассмотрим квадратную функцию f(x) = x^2. При приближении аргумента x к бесконечности, значения функции f(x) будут стремиться к положительной бесконечности. Таким образом, область значений этой функции - все неотрицательные числа.
Важно помнить, что в некоторых случаях функция может иметь ограничения, связанные с отрицательными или нулевыми значениями аргументов. В таких случаях нужно учитывать эти ограничения при определении области значений функции.
Что такое область значений математических функций?

Для понимания области значений функции необходимо знать ее определение области значений функции. Определение области значений определяет ограничения, которые накладываются на значения функции в зависимости от ее аргументов.
Область значений может быть ограничена или неограничена. Если функция не имеет ограничений на значения, которые она может принимать, то ее область значений считается неограниченной.
Например, для функции y = x^2 область значений будет все положительные числа и ноль, так как квадрат любого числа будет положительным или нулем.
Знание области значений функции позволяет определить, какие значения функции могут быть получены при ее использовании в конкретной ситуации. Это полезно, например, при решении уравнений или задач, требующих поиска максимального или минимального значения функции.
Понятие области значений

Для некоторых функций область значений может быть ограничена определенным интервалом, например, если функция ограничена сверху и снизу. Например, область значений для функции f(x) = x^2 ограничена положительными числами и нулем.
В то же время, область значений для некоторых функций может быть неограничена. Например, функция f(x) = x^2 может принимать любые положительные значения и ноль.
Для некоторых функций область значений может быть дискретной, состоящей из отдельных значений. Например, область значений для функции f(x) = sin(x) – это все значения от -1 до 1, включая эти граничные значения.
Область значений функции тесно связана с ее областью определения, которая определяет, для каких значений аргументов функция имеет смысл. Знание области значений позволяет более полно описать поведение функции и использовать ее в различных математических моделях и задачах.
| Функция | Область значений |
|---|---|
| f(x) = x^2 | Все неотрицательные числа, включая ноль |
| f(x) = sin(x) | Все значения от -1 до 1, включая граничные значения |
| f(x) = 1/x | Все ненулевые действительные числа |
Значение функции
Для некоторых функций значение может быть числовым, например, в случае функции f(x) = x^2, значение для аргумента x=3 будет равно 9. Другие функции могут иметь значение из других типов данных, например, функция f(x) = "Привет, " + x будет иметь значение "Привет, мир!" для аргумента x="мир".
Определение области значений функции позволяет найти все возможные значения функции при изменении аргументов в определенном диапазоне. Для этого необходимо учитывать возможные ограничения и ограничители функции.
Значение функции имеет важное значение в математике, физике, экономике и других науках. Оно позволяет найти точки экстремума функции, решить уравнения и неравенства, а также проводить анализ и исследование функций в различных областях.
</p>
Примеры определения области значений

Определение области значений математических функций часто требует использования различных методов и концепций. Вот несколько примеров, чтобы помочь вам лучше понять эту тему:
Пример 1: Рассмотрим функцию f(x) = x^2. Чтобы определить область значений этой функции, мы замечаем, что квадрат любого числа всегда положителен или ноль. Следовательно, область значений функции f(x) = x^2 - все положительные числа и ноль.
Пример 2: Рассмотрим функцию g(x) = sin(x). Функция синуса может принимать значения от -1 до 1. Таким образом, область значений функции g(x) - все числа от -1 до 1.
Пример 3: Рассмотрим функцию h(x) = 1 / (x - 3). Здесь необходимо исключить значение x = 3, так как это приведет к делению на ноль. Поэтому область значений функции h(x) - все числа, кроме 3.
Пример 4: Рассмотрим функцию k(x) = sqrt(x). Функция квадратного корня может принимать только положительные значения, поэтому область значений функции k(x) - все положительные числа и ноль.
Это лишь некоторые примеры, которые помогут вам начать определение области значений математических функций. Удачи в вашем математическом путешествии!
Определение области значений сложных функций

При определении области значений сложных функций необходимо учитывать особенности каждой составляющей функции. В общем случае, область значений сложной функции будет зависеть от областей значений входных функций и операций, применяемых к ним.
Если функция является композицией двух функций, необходимо учитывать, какие значения может принимать внутренняя функция на своей области определения, и какие значения может принимать внешняя функция на области значений внутренней функции.
Для функций, содержащих операции сложения, вычитания, умножения и деления, область значений будет зависеть от областей значений входных функций и условий, наложенных на эти операции. Например, если входная функция имеет область значений вещественных чисел, а операция умножения применяется к вещественным числам, то область значений сложной функции будет также вещественными числами.
Однако, следует помнить, что определение области значений сложных функций может быть сложным и требовать дополнительных рассуждений и анализа. Например, функция может содержать условия, которые ограничивают область значений, или функция может быть определена только на определенных подмножествах области определения входных функций.
Чтобы визуализировать и описать область значений сложных функций, можно использовать таблицу. В таблице можно указать область определения входных функций, применяемые операции и их области действия, а также полученную область значений сложной функции.
| Входные функции | Операции | Область значений |
|---|---|---|
| функция A | операция 1 | область значений 1 |
| функция B | операция 2 | область значений 2 |
| ... | ... | ... |
| функция N | операция N-1 | область значений N-1 |
| сложная функция | операция N | область значений сложной функции |
Таким образом, определение области значений сложных функций требует внимательного анализа и учета всех составляющих функций и операций, чтобы выявить, какие значения может принимать итоговая функция.
Влияние параметров на область значений
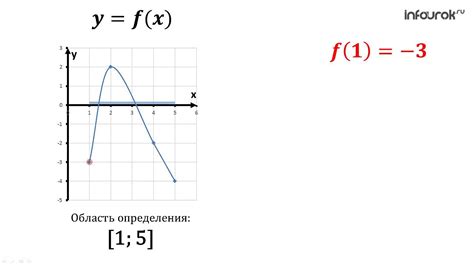
Область значений (или промежуток значений) математической функции определяет множество значений, которые может принять эта функция. Она позволяет нам понять, какие значения можно получить при заданных параметрах.
Параметры функции могут влиять на ее область значений. Изменение параметров может сужать или расширять область возможных значений функции.
Например, рассмотрим функцию f(x) = ax^2 + bx + c, где a, b и c - параметры функции.
Если a > 0, то функция будет иметь "улыбчатый" параболический график с ветвями, направленными вверх. В этом случае область значений функции будет положительными значениями и ноль.
Если a < 0, то функция будет иметь "грустный" параболический график с ветвями, направленными вниз. В этом случае область значений функции будет отрицательными значениями и ноль.
Значения параметров b и c также могут влиять на область значений. Например, при b = 0 и c = 0 функция становится квадратической функцией только с одной осью симметрии, а область значений функции будет положительными значениями и ноль.
Таким образом, изменение параметров функции может привести к различным областям значений. Понимание этих зависимостей помогает нам анализировать и понимать поведение математических функций.
Практическое применение определения области значений

Определение области значений математических функций играет важную роль в практическом применении математики. Зная область значений функции, мы можем более точно понять, как функция влияет на входные данные и какие значения она может принимать.
Практическое применение определения области значений особенно полезно в таких областях, как физика, экономика, финансы и компьютерные науки. В физике, например, область значений функции может помочь нам определить различные физические параметры, такие как диапазон движения, максимальное и минимальное значение и т. д. В экономике и финансах, область значений функции может помочь нам анализировать прибыль, потери, рост и т. д. В компьютерных науках, область значений функции может помочь нам определить диапазон работы программы, обработку входных данных и многое другое.
Определение области значений также может помочь увидеть, как разные значения входных данных влияют на выходные данные функции. Например, если функция имеет ограниченную область значений, это может означать, что определенные значения входных данных будут приводить к повторяющимся выходным данным. С другой стороны, если функция имеет бесконечную область значений, это может означать, что каждое значение входных данных будет соответствовать уникальному выходному значению.
Все это делает практическое применение определения области значений весьма полезным инструментом для анализа математических функций и их влияния на реальный мир.