Определение основания прямоугольного треугольника — способы и примеры

Прямоугольный треугольник - это треугольник, у которого один из углов равен 90 градусам. Данная геометрическая фигура находит широкое применение в различных областях науки и техники, и поэтому важно уметь определить основание этого треугольника. Основание прямоугольного треугольника - это сторона, которая лежит против прямого угла. Зная значение основания, можно легко решить задачи, связанные с прямоугольными треугольниками.

Определить основание прямоугольного треугольника можно различными методами. Один из них - использование теоремы Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Одним из катетов является основание треугольника, а другим - сторона, лежащая против прямого угла. Подставив известные значения в формулу и решив ее, можно найти длину основания.

Еще один способ определить основание прямоугольного треугольника - использование тригонометрических функций, таких как синус, косинус и тангенс. Если известны длины сторон треугольника и значение угла, противоположного основанию, можно воспользоваться соответствующими тригонометрическими формулами, чтобы найти длину основания.

Определение основания прямоугольного треугольника

Прямоугольный треугольник имеет один прямой угол, равный 90 градусов. Основание этого треугольника - это сторона, противолежащая прямому углу.

Для определения основания прямоугольного треугольника можно использовать теорему Пифагора. В этой теореме гипотенуза квадрату равна сумме квадратов катетов. Катеты - это две другие стороны треугольника, не являющиеся гипотенузой.

Если известны значения двух сторон прямоугольного треугольника, то с помощью теоремы Пифагора можно найти значение третьей стороны, которая является основанием.

Например, если длина одного катета равна 3 единицам, а длина гипотенузы равна 5 единицам, то с помощью теоремы Пифагора можно найти значение другого катета (основания):

3² + b² = 5²

9 + b² = 25

b² = 16

b = 4

Таким образом, основание прямоугольного треугольника в данном случае равно 4 единицам.

Зная основание и высоту, можно вычислить площадь прямоугольного треугольника по формуле S = (основание * высота) / 2.

Теперь вы знаете, как определить основание прямоугольного треугольника и применить этот навык для решения задач связанных с треугольниками и их площадями.

Основные методы для нахождения основания прямоугольного треугольника

Существуют несколько методов для определения основания прямоугольного треугольника:

1. Знание двух сторон треугольника и угла между ними. Если известны длины двух сторон треугольника и значение угла между ними, можно использовать тригонометрические функции (такие как синус, косинус и тангенс) для нахождения длины основания. Например, если известны сторона A, сторона B и угол между ними C, то основание (сторона, противоположная углу C) можно найти с помощью формулы: основание = A * sin(C) / sin(90° - C).
2. Использование теоремы Пифагора. Если известны длины двух сторон треугольника, которые образуют прямой угол, можно использовать теорему Пифагора для нахождения длины основания. Теорема Пифагора гласит, что квадрат длины гипотенузы (стороны, противоположной прямому углу) равен сумме квадратов длин других двух сторон. Таким образом, чтобы найти длину основания, можно воспользоваться формулой: основание = sqrt(A^2 - B^2), где A - гипотенуза, B - другая сторона.
3. Использование свойств прямоугольного треугольника. Прямоугольные треугольники имеют свойства, которые могут помочь в нахождении основания. Например, если известны длины катетов (других двух сторон, образующих прямой угол), то длину основания можно найти с помощью формулы: основание = sqrt(A^2 + B^2), где A и B - катеты.

Это лишь некоторые из основных методов, которые можно использовать для нахождения основания прямоугольного треугольника. В каждом конкретном случае выбор метода зависит от известных параметров и поставленной задачи.

Геометрическое определение основания прямоугольного треугольника

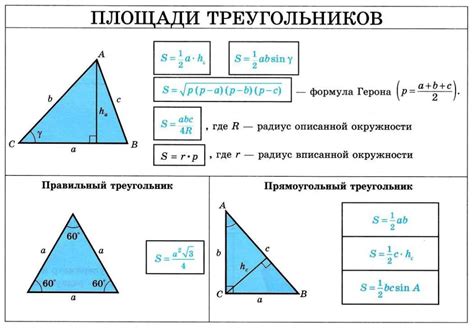
Геометрически, основание прямоугольного треугольника является основной горизонтальной стороной, расположенной ниже вершины прямого угла.

Важно отметить, что в прямоугольном треугольнике основание перпендикулярно гипотенузе и является его проекцией на горизонтальную ось.

Основание прямоугольного треугольника является важным параметром при решении задач, связанных с этой геометрической фигурой. Длина основания используется для вычисления различных параметров, таких как площадь, периметр и длина других сторон треугольника.

Понятие основания прямоугольного треугольника в геометрии

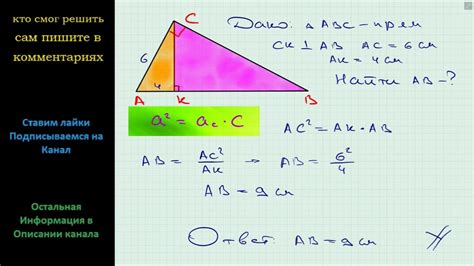
Основание прямоугольного треугольника является гипотенузой, то есть длинной стороной, противоположной прямому углу. Она соединяет вершину прямого угла с противоположным катетом и является самой длинной из всех сторон треугольника.

Понятие основания прямоугольного треугольника является важным для вычисления его площади. Формула для вычисления площади треугольника состоит из умножения половины основы на высоту, которая опускается на это основание и проходит через вершину прямого угла.

Также, основание прямоугольного треугольника играет роль в определении других характеристик треугольника, таких как периметр, углы и теоремы, связанные с его сторонами и углами.

Обратите внимание, что в прямоугольном треугольнике нет одного универсального основания, так как оно может быть любой из двух катетов (коротких сторон), в зависимости от контекста задачи или вычислений.

Тригонометрическое определение основания прямоугольного треугольника

Для определения основания прямоугольного треугольника можно использовать функции тригонометрии, такие как синус (sin), косинус (cos) и тангенс (tg). В данном случае основная формула выглядит следующим образом:

основание = прилежащая сторона * тангенс (угол)

Например, рассмотрим прямоугольный треугольник ABC, где угол А равен 30 градусам, а гипотенуза BC равна 10 см. Для определения основания треугольника необходимо использовать тангенс угла А. Подставим значения в формулу:

основание = BC * tg(A) = 10 * tg(30°)

основание = 10 * 0,577 = 5,77 см

Таким образом, основание прямоугольного треугольника ABC равно 5,77 см.

Тригонометрическое определение основания прямоугольного треугольника позволяет нам не только определить длину основания, но и решать различные задачи связанные с этим геометрическим объектом.

Методы нахождения основания с использованием тригонометрических функций

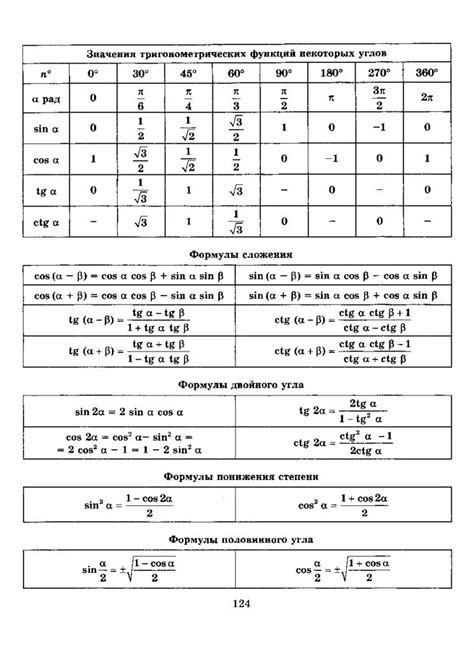
Для нахождения основания прямоугольного треугольника существует несколько методов, основанных на использовании тригонометрических функций. Эти методы позволяют найти длину основания при известной длине одного из катетов или при известных значениях угла и длины другого катета.

Первый метод основан на использовании тангенса угла треугольника. Если известна длина одного из катетов и значение тангенса угла между гипотенузой и этим катетом, то длину основания можно найти умножением значения тангенса на длину катета. Формула для этого выглядит следующим образом:

основание = катет * тангенс(угол)

Второй метод основан на использовании синуса угла треугольника. Если известна длина гипотенузы и значение синуса угла между гипотенузой и основанием, то длину основания можно найти делением значения синуса на длину гипотенузы. Формула для этого выглядит следующим образом:

основание = гипотенуза * синус(угол)

Третий метод основан на использовании косинуса угла треугольника. Если известна длина гипотенузы и значение косинуса угла между гипотенузой и основанием, то длину основания можно найти делением значения косинуса на длину гипотенузы. Формула для этого выглядит следующим образом:

основание = гипотенуза * косинус(угол)

Например, если известны длина гипотенузы AB и значение синуса угла ACB, то длину основания CB можно найти по формуле CB = AB * синус(ACB).

Примеры нахождения основания прямоугольного треугольника

Пример 1: Даны длины двух сторон прямоугольного треугольника a=5 и b=12. Необходимо найти длину основания треугольника c.

Решение: Воспользуемся теоремой Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. То есть c^2 = a^2 + b^2. Подставим известные значения: c^2 = 5^2 + 12^2 = 25 + 144 = 169. Извлекая квадратный корень из обоих частей уравнения, получаем, что c = 13.

Пример 2: Дан прямоугольный треугольник, у которого гипотенуза c=10, а один из катетов a=6. Необходимо найти длину основания треугольника b.

Решение: Снова применим теорему Пифагора: c^2 = a^2 + b^2. Подставим известные значения: 10^2 = 6^2 + b^2. Раскрыв скобки, найдем, что 100 = 36 + b^2. Вычтем 36 из обеих частей уравнения: 64 = b^2. Извлекая квадратный корень, получаем, что b = 8.

Это лишь два примера нахождения основания прямоугольного треугольника. Существуют и другие методы и формулы, включая тригонометрию, для решения подобных задач. Однако, основным инструментом является теорема Пифагора, которая обеспечивает простой и эффективный способ нахождения основания треугольника.