Трапеция - это геометрическая фигура с двумя параллельными сторонами, называемыми основаниями. Основание трапеции - один из ее наибольших параметров, и его не всегда просто найти. Однако, с помощью средней линии и периметра трапеции, можно определить значение основания и решить поставленную задачу.
Средняя линия трапеции - это отрезок, соединяющий середины ее непараллельных сторон. Она делит основание трапеции на две равные части и параллельна ему. Зная длину средней линии и периметр трапеции, можно найти длину каждого из оснований и, таким образом, определить основание, которое требуется найти.
Для решения этой задачи необходимо использовать формулу для периметра трапеции, которая выглядит следующим образом:
Периметр = a + b + c + d,
где a и b - основания трапеции, c и d - боковые стороны. Также известно, что сумма длин оснований равна периметру минус два боковые стороны:
a + b = Периметр - c - d.
Используя известные данные о периметре и средней линии, можно найти длину каждого из оснований с помощью простых алгебраических операций.
Следуя простому алгоритму, определите искомое значение
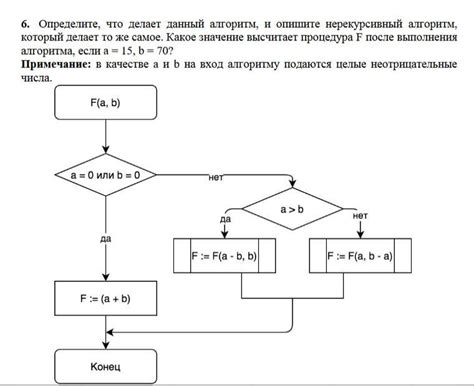
Для определения основания трапеции через среднюю линию и периметр, следуйте следующему алгоритму:
Шаг 1: Найдите сумму длин оснований трапеции, умножив периметр на половину разности между средней линией и суммой высот трапеции. Полученный результат разделите на сумму длин оснований.
Шаг 2: Из полученного значения вычтите половину разности между средней линией и суммой высот трапеции.
Шаг 3: Полученное значение будет являться основанием трапеции.
Используя этот простой алгоритм, вы сможете определить основание трапеции через среднюю линию и периметр с большой точностью.
Определение ключевых понятий трапеции
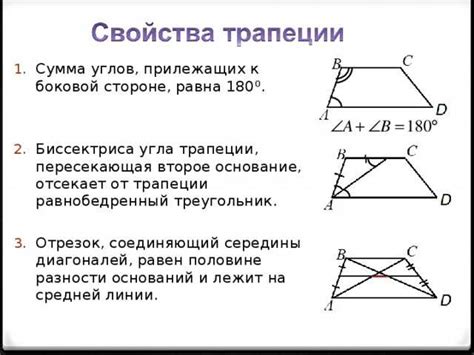
Основания трапеции - две параллельные стороны трапеции, которые имеют разную длину.
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции.
Высота трапеции - это перпендикуляр, проведенный из вершины трапеции к основанию трапеции или к его продолжению.
Периметр трапеции - это сумма всех сторон трапеции.
Площадь трапеции - это произведение полусуммы длин оснований трапеции на ее высоту. Формула для вычисления площади трапеции: S = ((a + b) * h) / 2, где a и b - длины оснований трапеции, h - высота.
Изучение ключевых понятий трапеции поможет лучше понять ее свойства и использовать эти знания при решении задач, включающих периметр и площадь трапеции.
Формула для нахождения длины средней линии
Для нахождения длины средней линии трапеции, мы можем использовать следующую формулу:
| Сумма длин оснований | 2 * (a + b) |
| Длина средней линии | --- |
| Периметр трапеции | p |
Формула для нахождения длины средней линии трапеции состоит в делении суммы длин оснований на 2. Также, можно использовать формулу, в которой длина средней линии определяется через периметр трапеции и сумму длин оснований, как (2 * p - a - b) / 2.
Нахождение длины средней линии является важным шагом в решении задач, связанных с трапециями, таких как вычисление площади или нахождение других характеристик фигуры.
Формула для нахождения периметра трапеции
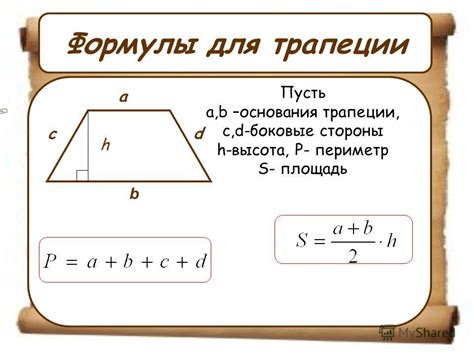
P = a + b + c + d
где P - периметр трапеции, a, b, c, d - длины сторон трапеции.
Из данной формулы следует, что для нахождения периметра необходимо сложить длины всех сторон трапеции. У стандартной трапеции длины оснований могут быть различными, а длины боковых сторон - равными. Однако в общем случае длины всех сторон могут отличаться друг от друга.
Зная формулу для нахождения периметра трапеции, можно расчитать сумму всех сторон и таким образом найти периметр данной фигуры. Это позволяет решить задачи, связанные с нахождением периметра трапеции.
Подставьте найденные значения в уравнение

Теперь, когда мы нашли значения для средней линии (m) и периметра (P), мы можем подставить их в уравнение для трапеции. Уравнение для трапеции имеет вид:
P = a + b + 2m
Где P - периметр трапеции, a и b - основания, m - средняя линия.
Подставляя найденные значения в данное уравнение, получаем:
| Периметр (P) | Основание a | Основание b | Средняя линия (m) |
|---|---|---|---|
| P = 40 | a = 12 | b = 16 | m = 7 |
Подставляем значения в уравнение:
40 = 12 + 16 + 2 * 7
40 = 12 + 16 + 14
Выразите основание трапеции через среднюю линию и периметр
Для начала вспомним, что средняя линия трапеции – это линия, соединяющая середины боковых сторон фигуры. Обозначим среднюю линию трапеции как м, а периметр – как Р.
Используя свойство средней линии трапеции, мы можем установить следующую зависимость между длинами оснований и длиной средней линии:
2м = сумма оснований
Таким образом, длина каждого основания трапеции равна полусумме длины средней линии и полупериметра фигуры:
Основание = (м + Р/2) / 2
Итак, для нахождения длины основания трапеции, нам необходимо знать длину средней линии и периметр фигуры.