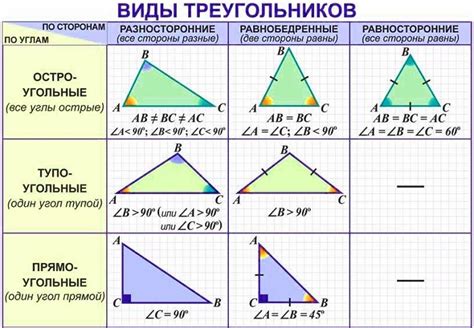
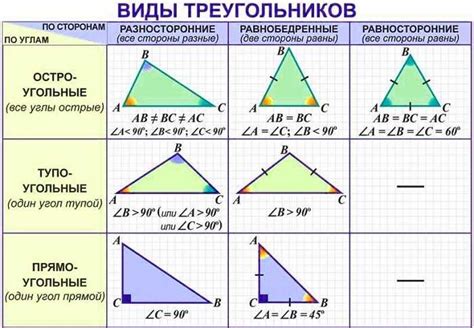
Треугольник – это геометрическая фигура, обладающая тремя сторонами и тремя углами. Такие треугольники могут быть различных типов, в зависимости от величины их углов. Одним из наиболее интересных типов является остроугольный треугольник, в котором все три угла меньше 90 градусов. Интересно, как можно определить, является ли треугольник остроугольным по заданным сторонам?
Вам понадобятся основные знания геометрии и тригонометрии, чтобы разобраться в этом вопросе. Но не беспокойтесь, все необходимое будет представлено в доступной форме. Ключевым моментом в определении остроугольности треугольника является нахождение его углов.
Если вам известны длины всех трех сторон треугольника, вы можете использовать закон косинусов для вычисления углов. Нужно применить формулу, которая позволяет выразить косинус угла через длины сторон треугольника. Затем, используя тригонометрическую функцию арккосинус, вычислить значения углов. Если все три угла треугольника окажутся меньше 90 градусов, то он будет остроугольным.
Остроугольный треугольник: определение и свойства
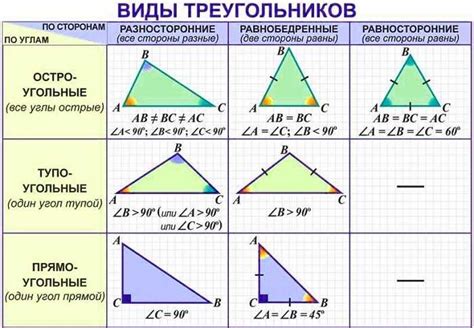
Остроугольным треугольником называется треугольник, у которого все его углы острые. Если в треугольнике все его углы острые, то такой треугольник считается остроугольным.
Свойства остроугольного треугольника:
- В остроугольном треугольнике все его углы меньше 90 градусов. Это означает, что ни один из углов треугольника не является прямым или тупым.
- Сумма всех углов остроугольного треугольника равна 180 градусов.
- В остроугольном треугольнике все его стороны положительные и взаимно отличаются по длине.
- Основание высоты остроугольного треугольника всегда лежит внутри самого треугольника.
- Остроугольный треугольник всегда является выпуклым, то есть все его углы направлены в одну сторону (внутрь треугольника).
- Остроугольный треугольник может быть разносторонним, равнобедренным или разносторонним.
Остроугольные треугольники являются наиболее распространенными и необычайно интересными фигурами в геометрии. Их свойства и особенности широко используются в различных областях математики, физики, и других наук.
Что такое остроугольный треугольник?
В остроугольном треугольнике каждая из трех сторон имеет длину. Математическим обозначением для сторон остроугольного треугольника являются a, b и c. Сумма длин двух сторон треугольника должна быть больше длины третьей стороны по неравенству треугольника. Это требование гарантирует, что треугольник является замкнутой фигурой.
Остроугольные треугольники являются наиболее распространенными типами треугольников и обладают множеством интересных свойств. Они используются в различных областях науки и техники, таких как геометрия, физика, строительство и дизайн.
Очень важно уметь определить, является ли треугольник остроугольным по заданным сторонам. Это можно сделать, используя теорему косинусов. Согласно этой теореме, если квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними, то треугольник остроугольный.
Пружина или спрашивала? Как определить остроугольный треугольник?
Правило треугольника гласит, что сумма длин двух сторон треугольника всегда должна быть больше длины третьей стороны. Если это условие выполняется для всех трех комбинаций сторон, то треугольник является остроугольным.
Для лучшего понимания этого правила, можно визуализировать его с помощью таблицы:
| Сторона A | Сторона B | Сторона C | Остроугольный треугольник? |
|---|---|---|---|
| Да | Да | Да | Да |
| Да | Да | Нет | Нет |
| Да | Нет | Да | Нет |
| Да | Нет | Нет | Нет |
| Нет | Да | Да | Нет |
| Нет | Да | Нет | Нет |
| Нет | Нет | Да | Нет |
| Нет | Нет | Нет | Нет |
Если вы заполнили таблицу и в последнем столбце получили "Да" для всех комбинаций сторон, то треугольник является остроугольным.
Теперь, когда вы знаете, как определить остроугольный треугольник по сторонам, необходимо проверить соответствующий треугольник. Используйте это правило для расчета и проверки всех трех пар сторон. Если все стороны соответствуют правилам, треугольник будет остроугольным.
Какие свойства имеет остроугольный треугольник?
- У каждого из трех углов остроугольного треугольника мера меньше 90 градусов.
- Сумма всех углов остроугольного треугольника равна 180 градусов.
- Остроугольный треугольник имеет три острых угла, которые все смежные друг с другом. Ни один угол не может быть прямым или тупым.
- Стороны остроугольного треугольника можно классифицировать как короткие, так как они являются противолежащими острых углов.
- Остроугольный треугольник может быть правильным или неправильным в зависимости от того, равны ли все его стороны и углы.
Зная эти свойства, можно легко определить остроугольный треугольник, основываясь на измерениях его углов и сторон.
Остроугольный треугольник и его углы
Для определения остроугольного треугольника по сторонам необходимо знать значения длин всех трех сторон. Для этого можно использовать теорему косинусов.
Теорема косинусов гласит, что в любом треугольнике квадрат одной из сторон равен сумме квадратов двух остальных сторон, умноженных на два произведения этих сторон и косинуса между ними.
Таким образом, чтобы определить, является ли треугольник остроугольным, нам нужно проверить, выполняется ли следующее условие:
- Подставить значения длин сторон треугольника в теорему косинусов.
- Вычислить значение косинуса каждого угла, используя найденные значения длин сторон.
- Проверить, является ли каждый угол острым. Если для всех углов выполнено условие: косинус угла больше нуля, то треугольник является остроугольным.
Если треугольник является остроугольным, то его углы будут острыми, а сумма всех трех углов будет равна 180 градусов.
Теперь вы знаете, как определить остроугольный треугольник и вычислить его углы.
Остроугольный треугольник и его стороны
Каждая сторона треугольника имеет свою длину. Обозначим стороны треугольника как a, b и c. Чтобы треугольник был остроугольным, его стороны должны удовлетворять следующему условию:
| Сторона | Условие |
|---|---|
| a | a^2 < b^2 + c^2 |
| b | b^2 < a^2 + c^2 |
| c | c^2 < a^2 + b^2 |
Если все стороны треугольника удовлетворяют этому условию, то треугольник является остроугольным. Если хотя бы одно из условий не выполняется, то треугольник будет прямоугольным или тупоугольным.
Зная длины сторон треугольника, можно использовать эти условия для определения его типа. Это может быть полезно при решении геометрических задач или при работе с треугольниками в программировании.
Остроугольный треугольник и его высоты
Высота – это отрезок, проведенный из вершины треугольника к противоположной стороне и перпендикулярный ей. Остроугольный треугольник имеет три высоты – каждая из вершин треугольника может быть основанием для высоты.
Высоты остроугольного треугольника пересекаются в одной точке, называемой ортоцентром. Ортоцентр может находиться как внутри треугольника, так и на его сторонах или даже вне треугольника в случае, когда угол треугольника больше 90 градусов.
Высоты остроугольного треугольника играют важную роль при решении различных геометрических задач. Они позволяют найти площадь треугольника, а также решить задачу о построении треугольника по заданным конструкциям.
Уравнения для высот остроугольного треугольника можно записать следующим образом:
- Высота, проведенная из вершины A, обладает следующим уравнением: hA = b × sin(A),
- Высота, проведенная из вершины B, обладает следующим уравнением: hB = a × sin(B),
- Высота, проведенная из вершины C, обладает следующим уравнением: hC = c × sin(C),
где hA, hB и hC – высоты треугольника, a, b и c – стороны треугольника, A, B и C – соответствующие углы.
Зная стороны остроугольного треугольника и углы, можно вычислить все его высоты и определить их длины с помощью указанных уравнений. Это позволит провести детальный анализ треугольника и использовать его свойства для решения задач.
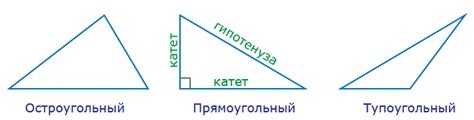
Остроугольный треугольник в тригонометрии
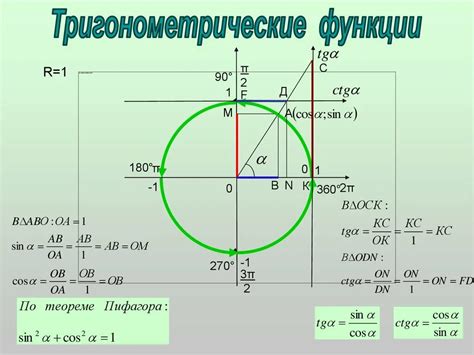
В тригонометрии, остроугольный треугольник имеет несколько уникальных свойств. Одно из главных свойств остроугольных треугольников - это то, что соотношение сторон в таком треугольнике связано с его углами при помощи тригонометрических функций.
В тригонометрии используются три основные тригонометрические функции: синус (sin), косинус (cos) и тангенс (tg). Они определены как отношения длин сторон треугольника.
Например, синус угла A в остроугольном треугольнике можно найти, разделив длину противолежащего стороне A катета на гипотенузу треугольника.
Также известно, что сумма всех трех углов в остроугольном треугольнике равна 180 градусов, что позволяет использовать теорему синусов и теорему косинусов для нахождения неизвестных сторон и углов.
Таким образом, в тригонометрии остроугольный треугольник играет важную роль, позволяя нам вычислять неизвестные значения сторон и углов треугольника, используя соотношения между ними и тригонометрическими функциями.
Примечание: Важно отметить, что остроугольный треугольник не является единственным типом треугольника, и есть и другие типы треугольников, например, прямоугольный и тупоугольный треугольники.
Примеры задач на определение остроугольного треугольника
Пример 1:
Дан треугольник со сторонами a = 4, b = 5 и c = 6. Проверить, является ли он остроугольным.
Решение:
Сначала проверим, существует ли треугольник с такими сторонами, используя неравенство треугольника: a + b > c, b + c > a, a + c > b. В данном случае: 4 + 5 > 6, 5 + 6 > 4 и 4 + 6 > 5, поэтому треугольник существует.
Теперь используем теорему косинусов: c^2 = a^2 + b^2 - 2ab*cos(C), где C - угол против стороны c.
Вычисляем значения: c^2 = 4^2 + 5^2 - 2*4*5*cos(C) = 16 + 25 - 40*cos(C) = 41 - 40*cos(C).
Так как a^2 + b^2 > c^2, то треугольник остроугольный. В данном случае, 4^2 + 5^2 > 6^2, поэтому треугольник остроугольный.
Пример 2:
Дан треугольник со сторонами a = 7, b = 8 и c = 5. Проверить, является ли он остроугольным.
Решение:
Сначала проверим, существует ли треугольник с такими сторонами, используя неравенство треугольника: a + b > c, b + c > a, a + c > b. В данном случае: 7 + 8 > 5, 8 + 5 > 7 и 7 + 5 > 8, поэтому треугольник существует.
Теперь используем теорему косинусов: c^2 = a^2 + b^2 - 2ab*cos(C), где C - угол против стороны c.
Вычисляем значения: c^2 = 7^2 + 8^2 - 2*7*8*cos(C) = 49 + 64 - 112*cos(C) = 113 - 112*cos(C).
Так как a^2 + b^2 < c^2, то треугольник тупоугольный. В данном случае, 7^2 + 8^2 < 5^2, поэтому треугольник не является остроугольным.
Таким образом, для определения остроугольного треугольника по его сторонам необходимо проверить неравенство треугольника и применить теорему косинусов.