Периодическая десятичная запись дроби - это такая десятичная запись, в которой определенная группа цифр постоянно повторяется. Для определения периода десятичной записи дроби существует специальный алгоритм.

Алгоритм определения периода десятичной записи дроби основан на делении числителя на знаменатель в столбик. Результат деления задается в виде целой части и десятичной дроби. Если дробная часть начинает повторяться, то это и есть период.

Например, рассмотрим дробь 1/3. При делении 1 на 3 получаем десятичную запись 0,3333... В данном случае число 3 бесконечно повторяется, что означает периодичность дроби 1/3.

Определение периода десятичной записи дроби может иметь свои особенности, как в случае с иррациональными дробями или числами, содержащими разный период в целой и дробной частях. Важно уметь правильно применять алгоритм и анализировать результаты, чтобы получить корректную периодическую десятичную запись дроби.

Определение периода десятичной записи дроби

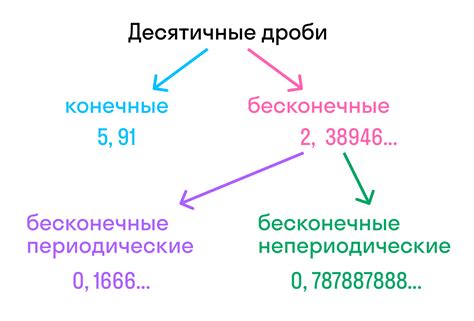
Периодом десятичной записи дроби называется последовательность цифр, которая повторяется бесконечно после десятичной точки. Для определения периода необходимо проанализировать десятичную запись дроби и найти повторяющуюся последовательность цифр.

Существуют различные алгоритмы для определения периода десятичной записи дроби. Один из них основан на делении числителя на знаменатель и анализе полученных остатков. Для примера рассмотрим дробь 1/3:

1 / 3 = 0.333333...

Здесь периодом является последовательность цифр 3, которая повторяется бесконечно. Для определения периода можно произвести деление числителя на знаменатель и записывать получаемые остатки, пока не встретится повторение:

Шаг 1: 1 / 3 = 0.3

Шаг 2: Переносим остаток 1 и записываем следующую цифру после десятичной точки: 1 → 10

Шаг 3: Делим полученное число 10 на 3: 10 / 3 = 3 (остаток 1)

Шаг 4: Переносим остаток 1 и записываем следующую цифру после десятичной точки: 1 → 10

Шаг 5: Делим полученное число 10 на 3: 10 / 3 = 3 (остаток 1)

Шаг 6: Повторяем шаги 4 и 5 до тех пор, пока не встретится повторение

В данном примере мы получили повторение последовательности остатков 1 → 10 → 1 → 10, что означает, что период десятичной записи дроби 1/3 равен 3.

Таким образом, для определения периода десятичной записи дроби необходимо произвести деление числителя на знаменатель и анализировать повторяющиеся остатки. Этот алгоритм может быть применен для любой десятичной дроби.

Алгоритм определения периода

Алгоритм определения периода дроби следующий:

1. Преобразуем дробь в десятичную запись.
2. Находим первую цифру после запятой и обозначаем ее как a.
3. Далее, вместо письменного деления, умножаем a на 10 и делим на исходную дробь.
4. Находим следующую цифру после запятой и обозначаем ее как b.
5. Повторяем шаг 3 и 4 до тех пор, пока не получим повторение цифр после запятой.

Например, рассмотрим запись дроби 1/3:

• 1/3 = 0.(3)
• Шаг 2: a = 3
• Шаг 3: 3 * 10 / 3 = 10; b = 1
• Шаг 4: 1 * 10 / 3 = 3; b = 3
• Получили повторение 3.

Таким образом, периодическая десятичная запись дроби 1/3 равна 0.(3).

Алгоритм определения периода десятичной записи дроби позволяет точно избавиться от неопределенного количества незначащих нулей и определить периодическую последовательность цифр в записи дроби.

Примеры периода десятичной записи дробей

• Дробь 1/3 имеет период 3: 0.3333...
• Дробь 1/7 имеет период 142857: 0.142857142857...
• Дробь 2/11 имеет период 18: 0.181818181818...
• Дробь 5/8 имеет период 625: 0.625625625...
• Дробь 1/6 имеет период 6: 0.166666...

Это лишь некоторые примеры, и в действительности периоды могут быть более длинными. Отличительной чертой дробей с периодом является повторение определенной последовательности цифр в их десятичной записи.