Определение положения точки на прямой является одним из основных понятий в математике. Эта концепция позволяет нам понять, находится ли точка слева или справа от другой точки на прямой. Это важное умение, которое применяется в различных областях, таких как геометрия, геодезия, физика и многое другое.
Для определения положения точки на прямой необходимо использовать понятие направления. Направление - это вектор, который указывает на то, находится ли точка слева или справа от другой точки. Вектор направления состоит из координатной оси и значения, которое определяет, в каком направлении находится точка.
Например, представим себе прямую и две точки на ней - A и B. Для определения положения точки C относительно точек A и B, необходимо вычислить значения векторов направления AC и BC. Если значение вектора направления AC положительное, значит точка C находится слева от точки A. Если значение отрицательное, то точка C находится справа от точки A. Аналогичным образом, вычисляем значение вектора направления BC. Если оно положительное, то точка C находится слева от точки B, если отрицательное - справа от точки B.
В этой статье мы рассмотрим несколько примеров, чтобы более полно понять процесс определения положения точки на прямой. Мы также рассмотрим основные правила и формулы, которые помогут вам легко определить положение точки на прямой в различных ситуациях.
Что такое положение точки на прямой
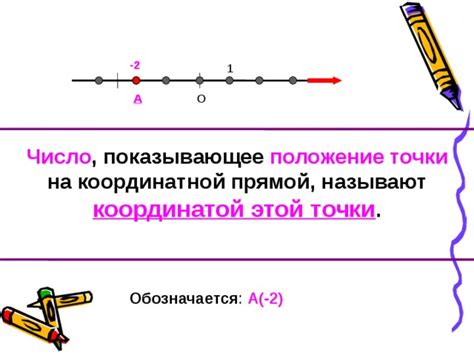
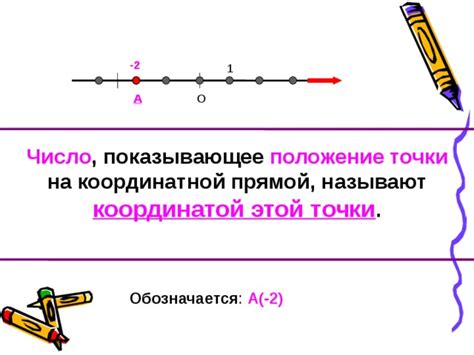
Чтобы определить положение точки на прямой, необходимо знать координату этой точки. Координата точки - это числовое значение, которое показывает расстояние от точки отсчета до точки. Обычно точкой отсчета является ноль, и положительные значения находятся справа от нуля, а отрицательные значения - слева от нуля.
Если координата точки больше нуля, то точка находится справа от точки отсчета. Если координата точки равна нулю, то точка находится на точке отсчета. Если координата точки меньше нуля, то точка находится слева от точки отсчета.
Пример:
| Точка | Координата | Положение на прямой |
|---|---|---|
| Точка A | 3 | Справа от точки отсчета |
| Точка B | 0 | На точке отсчета |
| Точка C | -2 | Слева от точки отсчета |
Положение точки на прямой имеет большое значение в геометрии и математике, и оно используется для решения различных задач и проблем, связанных с прямыми и их отношениями.
Зачем нужно определять положение точки на прямой
Знание положения точки на прямой позволяет определить, находится ли она слева или справа от другой точки или отрезка. Это может быть полезно при решении задач, связанных с расстоянием между точками или нахождением точки пересечения прямых.
Определение положения точки на прямой также используется для решения задач в физике, экономике и других науках. Например, при моделировании движения тела в пространстве или при исследовании графиков функций.
Для определения положения точки на прямой можно использовать различные методы, включая геометрические и алгебраические подходы. Знание этих методов и умение применять их позволяют решать задачи, требующие определения положения точки на прямой, с высокой точностью.
Таким образом, определение положения точки на прямой играет важную роль не только в геометрии и математике, но и находит применение в различных научных и практических областях. Умение определять положение точки на прямой помогает анализировать и решать задачи, связанные с пространством, движением и функциями.
Определение положения точки на прямой
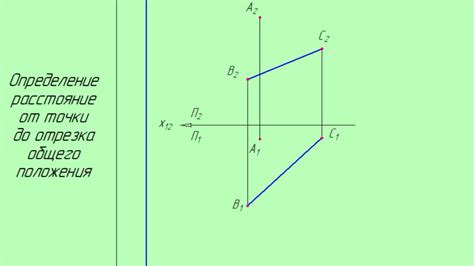
Для определения положения точки на прямой можно использовать несколько методов. Один из таких методов – использование координатных осей и алгебраических выражений.
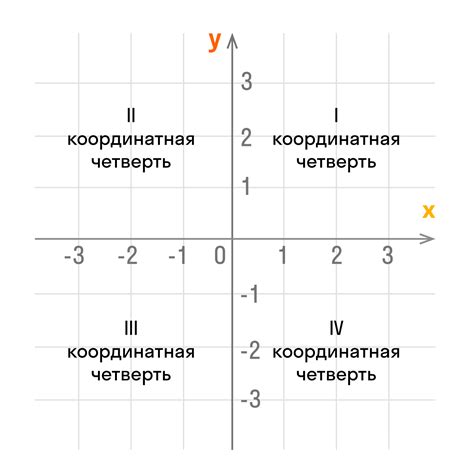
Представим прямую на координатной плоскости с осью абсцисс (ось X) и осью ординат (ось Y). У каждой точки на плоскости есть свои координаты – абсцисса (X) и ордината (Y).
Чтобы определить положение точки на прямой, нужно сравнить значение абсциссы точки с координатами прямой. Если абсцисса точки больше или равна левой границе прямой и меньше или равна правой границе прямой, то точка находится на прямой.
Если абсцисса точки меньше левой границы прямой, то точка лежит левее прямой. Если абсцисса точки больше правой границы прямой, то точка лежит правее прямой.
Определение положения точки на прямой может быть полезно для решения различных задач. Например, в геометрии, если нужно проверить, принадлежит ли точка отрезку, или в программировании, когда нужно определить, находится ли точка в заданном диапазоне значений.
Важно учитывать, что определение положения точки на прямой может варьироваться в зависимости от конкретной задачи и способа представления прямой на плоскости.
Использование методов определения положения точки на прямой позволяет производить точные вычисления и принимать решения на основе данной информации.
Пример: точка находится слева от прямой
Представим себе прямую линию на плоскости. На этой линии выберем две точки, которые будут служить нам ориентирами: точку A и точку B. Допустим, точка A находится слева от точки B.
Теперь давайте рассмотрим третью точку C, которая может находиться где угодно на плоскости. Наша задача - определить, находится ли точка C слева от прямой, проходящей через точки A и B, или нет.
Чтобы это сделать, мы можем посмотреть на положение точки C относительно вектора, направленного из точки A в точку B. Если точка C находится слева от этого вектора, то она также находится слева от прямой.
Чтобы определить положение точки C относительно вектора AB, мы можем воспользоваться формулой для вычисления векторного произведения двух векторов:
AB × AC = (xB - xA)(yC - yA) - (yB - yA)(xC - xA)
Если результат этого вычисления положительный, то точка C находится слева от прямой. Если результат отрицательный, то точка C находится справа от прямой.
Пример: точка находится справа от прямой
Предположим, что у нас есть прямая и точка, и нам нужно определить, находится ли эта точка справа от прямой. Для этого мы можем использовать следующий алгоритм:
- Найти уравнение прямой вида y = mx + b, где m - коэффициент наклона прямой, b - свободный член.
- Подставить координаты точки в уравнение прямой и получить значение y.
- Если полученное значение y больше или равно 0, то точка находится справа от прямой. Если значение y меньше 0, то точка находится слева от прямой.
Давайте рассмотрим пример:
У нас есть прямая с уравнением y = 2x + 3 и точка с координатами (2, 5). Чтобы определить, находится ли эта точка справа от прямой, подставим ее координаты в уравнение:
y = 2 * 2 + 3 = 7
Полученное значение y равно 7, что больше 0. Значит, точка (2, 5) находится справа от прямой y = 2x + 3.
Таким образом, можно определить положение точки относительно прямой, используя уравнение прямой и подстановку координат точки.
Пример: точка находится на прямой
Рассмотрим пример, чтобы увидеть, как определить положение точки на прямой. Пусть имеется прямая АВ и точка С.
Для определения положения точки на прямой, мы можем использовать операцию сравнения. Рассмотрим в данном примере расположение точки С относительно прямой АВ:
1) Если точка С находится на прямой АВ, то мы можем записать это так: С АВ.
2) Если точка С расположена слева от прямой АВ, то мы можем записать это так: С АВ.
3) Если точка С расположена справа от прямой АВ, то мы можем записать это так: С АВ.
Таким образом, у нас есть различные варианты, в которых мы можем записать положение точки С относительно прямой АВ. Используя эти операции сравнения, мы можем определить, находится ли точка на прямой или в каком направлении она находится от нее.
Пример: точка находится выше прямой
Предположим, что у нас есть прямая, заданная уравнением y = 2x + 3. Также дана точка А с координатами (2, 5). Чтобы определить положение точки А относительно прямой, можно подставить ее координаты в уравнение прямой и сравнить полученное значение с координатой y точки.
Для этого запишем уравнение прямой в виде y = f(x) = 2x + 3. Подставим x = 2:
y = 2 * 2 + 3 = 4 + 3 = 7.
Полученное значение y = 7 больше координаты y точки А (5), что означает, что точка находится выше прямой.
Пример: точка находится ниже прямой
Рассмотрим пример. Пусть задана прямая с уравнением y = 2x + 1, а также дана точка A с координатами (3, 4).
Для определения положения точки относительно прямой можно построить параллельную прямую, проходящую через точку A. Зная, что параллельные прямые имеют одинаковый угловой коэффициент, получаем уравнение новой прямой: y = 2x + b. Для нахождения коэффициента b подставим координаты точки A в уравнение: 4 = 2 * 3 + b, откуда b = -2.
Таким образом, уравнение новой прямой, проходящей через точку A, будет иметь вид y = 2x - 2.
Пример: точка находится в области между двумя прямыми
Для определения положения точки на прямой между двумя другими точками или прямыми, необходимо использовать понятие отрезка.
Допустим, у нас есть две прямые, заданные уравнениями y = 2x + 1 и y = -2x - 1. Мы хотим проверить, находится ли точка (3, 5) между этими прямыми.
Чтобы это сделать, мы можем подставить координаты точки в уравнения прямых и сравнить полученные значения. Если значение y находится между значениями для первой и второй прямых, значит, точка находится в области между ними.
Для первой прямой:
y = 2x + 1
y = 2(3) + 1 = 7
Для второй прямой:
y = -2x - 1
y = -2(3) - 1 = -7
Значение y для точки (3, 5) равно 5, что находится между 7 и -7. Следовательно, точка (3, 5) находится в области между первой и второй прямыми.
Таким образом, с использованием уравнений прямых и понятия отрезка, мы можем определить положение точки на прямой и в данном случае установить, что точка (3, 5) находится в области между двумя заданными прямыми.