Определение принадлежности точки треугольнику является одной из важных задач в геометрии. Это задача, которая может быть применена в различных областях, таких как компьютерная графика, компьютерное зрение, а также в разработке алгоритмов для решения сложных геометрических задач. Понимание, как определить, находится ли точка внутри треугольника или на его границе, важно для решения многих практических задач.
Существует несколько эффективных методов и алгоритмов для определения принадлежности точки треугольнику. Один из таких методов основан на использовании алгоритма пересечения луча с границей треугольника. Суть метода заключается в том, чтобы провести луч извне треугольника через данную точку и посчитать количество пересечений этого луча с границей треугольника. Если количество пересечений равно 1, то точка находится внутри треугольника, если 0 - точка вне треугольника, если 2 - точка на границе треугольника.
Другой метод основан на использовании координатной плоскости и алгоритме, который позволяет обойти все вершины треугольника и проверить, находится ли точка справа от каждого из ребер треугольника или слева. Если точка находится справа от каждого из ребер, то она находится внутри треугольника. Если точка находится слева от хотя бы одного из ребер, то она находится вне треугольника.
В данной статье будут подробно рассмотрены эти методы и алгоритмы, а также их применение в различных сферах. Будут приведены примеры кода на различных языках программирования, чтобы помочь читателям разобраться и применить эти методы и алгоритмы в своих проектах. Использование этих эффективных методов и алгоритмов позволит выяснить принадлежность точки треугольнику с высокой точностью и скоростью, что является важным в различных областях науки и инженерии.
Методы определения принадлежности точки треугольнику
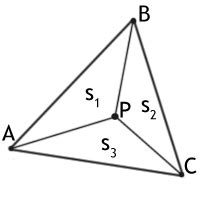
Существует несколько эффективных методов определения, лежит ли точка внутри треугольника или на его границе.
Один из таких методов - метод вычисления ориентации точек. Он основан на том, что треугольник разделяет плоскость на две полуплоскости - положительную и отрицательную. Если точка лежит внутри треугольника, то ориентации всех трех пар точек (A, B, P), (B, C, P) и (C, A, P) будут одинаковыми, где A, B и C - вершины треугольника, а P - проверяемая точка. Этот метод можно эффективно реализовать с использованием векторных операций и скалярного произведения.
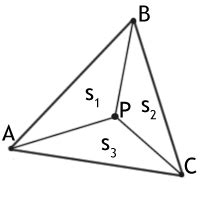
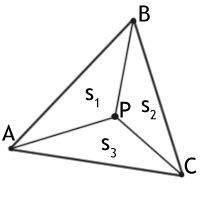
Другим методом является использование барицентрических координат. Барицентрические координаты точки P - это координаты (u, v, w), которые удовлетворяют следующим условиям: u + v + w = 1, и каждая координата является относительной площадью треугольников, образованных вершинами A, B, C и P. Если все координаты положительны, то точка P лежит внутри треугольника. Этот метод также позволяет находить положение точки относительно сторон и углов треугольника.
Еще один метод - это использование минимум-максимум теста. Он основан на том, что для каждой стороны треугольника существует линейное уравнение, которое определяет положение точки относительно этой стороны. Если точка P удовлетворяет условию всех трех уравнений, то она лежит внутри треугольника.
В таблице ниже приведено сравнение эффективности и точности этих методов:
| Метод | Эффективность | Точность |
|---|---|---|
| Метод ориентации точек | Высокая | Высокая |
| Барицентрические координаты | Средняя | Высокая |
| Минимум-максимум тест | Низкая | Средняя |
Выбор метода определения принадлежности точки треугольнику зависит от требований к эффективности и точности алгоритма, а также от сложности треугольника и количества проверяемых точек.
Алгоритмы для определения принадлежности точки треугольнику
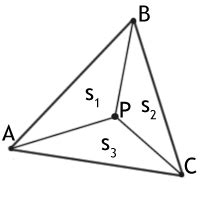
Один из простых алгоритмов для определения принадлежности точки треугольнику основан на использовании барицентрических координат. Для этого треугольник разбивается на три подтреугольника, образованных точкой, одним из вершин и противоположной стороной. Затем для каждого подтреугольника вычисляются его барицентрические координаты, которые определяются как отношения площадей подтреугольников к площади исходного треугольника. Если все барицентрические координаты лежат в интервале [0,1], то точка находится внутри треугольника.
Другой эффективный алгоритм для определения принадлежности точки треугольнику основан на использовании ориентированных площадей треугольников. Для этого вычисляются ориентированные площади треугольников, образованных точкой и двумя его вершинами. Затем суммируются ориентированные площади и сравниваются с площадью исходного треугольника. Если сумма равна площади треугольника, то точка находится внутри треугольника.
Также существуют алгоритмы, основанные на использовании векторного произведения. Для этого треугольник разбивается на три подтреугольника, образованных точкой и двумя его вершинами. Затем вычисляются векторные произведения этих трех подтреугольников. Если все векторные произведения имеют одинаковый знак, то точка находится внутри треугольника.
Кроме того, существуют и другие алгоритмы, основанные на комбинации различных методов, таких как алгоритм Мёллера-Трумбора или алгоритм Плиско. Эти алгоритмы обладают высокой точностью и производительностью, что позволяет эффективно определить принадлежность точки треугольнику даже в больших моделях.
Геометрический подход к определению принадлежности точки треугольнику
Один из наиболее эффективных геометрических подходов к решению этой задачи основан на использовании барицентрических координат. Барицентрические координаты точки в треугольнике позволяют выразить ее положение относительно вершин треугольника.
Пусть у нас есть треугольник ABC и точка P с координатами (x, y). Чтобы определить, находится ли точка P внутри треугольника, необходимо проверить, лежит ли она строго внутри каждой из сторон треугольника.
Для этого можно воспользоваться следующим алгоритмом:
- Вычислить площадь треугольника ABC.
- Вычислить площади треугольников PAB, PBC и PAC.
- Если сумма площадей треугольников PAB, PBC и PAC равна площади треугольника ABC, то точка P находится внутри треугольника. Иначе, точка P не принадлежит треугольнику.
Данный метод определения принадлежности точки треугольнику позволяет эффективно решить задачу без необходимости работы с уравнениями прямых и окружностей. Использование барицентрических координат позволяет упростить вычисления и повысить скорость алгоритма.
Аналитический подход к определению принадлежности точки треугольнику
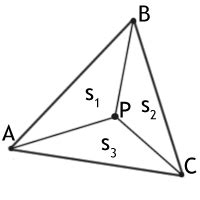
Аналитический подход основан на использовании уравнений прямых, на которых лежат стороны треугольника, и проверке условий, которым должна удовлетворять точка, чтобы принадлежать этому треугольнику.
Предположим, у нас есть треугольник ABC и точка P. Для определения принадлежности точки P треугольнику ABC, мы можем использовать следующий алгоритм:
- Найдем уравнения прямых, на которых лежат стороны треугольника ABC. Это можно сделать, используя формулу наклона прямой: y = mx + b, где m - наклон, а b - смещение.
- Проверим, лежит ли точка P левее или правее каждой из сторон треугольника ABC. Это можно сделать, подставляя координаты точки P в уравнения прямых и сравнивая результат с координатами точек A, B и C.
- Если точка P лежит слева от всех сторон или справа от всех сторон треугольника ABC, то точка P не принадлежит треугольнику.
- Если точка P лежит справа от одной стороны и слева от двух других сторон, или наоборот, то точка P принадлежит треугольнику.
Аналитический подход к определению принадлежности точки треугольнику позволяет эффективно определить, находится ли точка внутри треугольника или за его пределами. Этот метод имеет сложность O(1), то есть не зависит от размеров треугольника и точности вычислений.
Практическое применение методов и алгоритмов определения принадлежности точки треугольнику
В компьютерной графике, например, применение таких методов позволяет определить, находится ли точка внутри треугольника, что может быть полезно при отрисовке трехмерных моделей, создании анимаций или 3D игр. Это также может быть полезно при обрабатывании пользовательского ввода, например, для определения, на которую плоскость или объект кликнул пользователь.
В геометрии и картографии алгоритмы определения принадлежности точки треугольнику помогают в определении, находится ли произвольная точка внутри границ территории или находится ли объект на трассе маршрута. Это может быть полезно при построении карт, навигационных приложений или в геодезии.
В робототехнике применение данных методов помогает роботу определить свое местоположение относительно опорных точек или преград, что позволяет автономным роботам избегать столкновений или следовать заданным маршрутам. Это может быть полезно при проектировании и программировании роботов-пылесосов, беспилотных автомобилей или помощников на производстве.
Разработка и применение эффективных методов и алгоритмов определения принадлежности точки треугольнику является важным направлением исследований в различных областях. Улучшение точности и скорости таких алгоритмов позволяет решать сложные задачи более эффективно, повышая производительность и качество различных приложений и систем.
Преимущества и недостатки различных методов определения принадлежности точки треугольнику
- Метод пересечения ребер: этот метод основан на проверке пересечения точки с каждым из ребер треугольника. Преимуществом данного метода является его простота и относительно невысокая вычислительная сложность. Однако, недостатком является необходимость проверки пересечения с каждым ребром, что может занимать значительное количество времени при большом количестве треугольников.
- Метод барицентрических координат: данный метод основан на представлении точки как линейной комбинации барицентрических координат вершин треугольника. Этот метод обладает высокой точностью и сравнительно небольшой вычислительной сложностью. Однако, недостатком данного метода является большая вероятность ошибки, если точка находится на границе треугольника или на его вершинах.
- Метод использования ориентации треугольника: этот метод основан на определении ориентации треугольника при заданной точке. Если точка находится с одной стороны от каждого из ребер треугольника, то она принадлежит ему. Преимуществом данного метода является его высокая точность и низкая вычислительная сложность. Однако, недостатком является необходимость вычисления ориентации для каждого треугольника, что может занимать некоторое время при большом количестве треугольников.
Таким образом, каждый из представленных методов имеет свои преимущества и недостатки, и выбор конкретного метода определения принадлежности точки треугольнику зависит от требований к точности, вычислительной сложности и ожидаемому количеству операций.