Программирование является мощным инструментом, который позволяет нам решать различные математические задачи. Одной из таких задач является определение произведения вектора на число. Вектор - это математический объект, который имеет как направление, так и длину. Оно широко используется в физике, математике и других науках для описания различных физических явлений и процессов.
Векторное умножение на число - это операция, при которой каждая компонента вектора умножается на заданное число. В результате получается новый вектор, который имеет ту же направленность, но имеет измененную длину. Это может быть полезно, например, при изменении масштаба изображения или при применении физических законов, которые требуют изменения значения вектора.
В языке программирования Python определение произведения вектора на число достаточно простое. Мы можем использовать цикл или списковое выражение, чтобы умножить каждую компоненту вектора на число и сохранить результаты в новый вектор. Кроме того, Python предлагает библиотеки для работы с векторами, такие как NumPy, которые предоставляют готовые функции для выполнения этой операции.
Зачем нужно определение произведения вектора на число в Python?

Произведение вектора на число позволяет масштабировать или изменять длину и направление вектора. Эта операция особенно полезна при работе с графиками и визуализациями, где необходимо визуально изменять масштаб объектов, чтобы лучше их понять и проанализировать.
Кроме того, определение произведения вектора на число позволяет выполнять различные линейные преобразования, такие как сжатие, растяжение, поворот и смещение, которые могут быть полезными при решении задач оптимизации, моделировании физических процессов или создании анимаций.
Python предоставляет удобные инструменты для работы с векторами и числами, что делает определение произведения вектора на число простым и эффективным. Библиотеки, такие как NumPy и SciPy, предлагают множество функций и методов для работы с векторами и матрицами, включая операции скалярного умножения, сложения и вычитания.
В целом, определение произведения вектора на число является важным инструментом в программировании и анализе данных, который позволяет выполнять различные операции с векторами и получать нужные результаты. Понимание и использование этой операции поможет улучшить эффективность и точность ваших программ и аналитических решений.
Произведение вектора на число в Python: определение и применение

Определение: произведение вектора на число представляет собой умножение каждого элемента вектора на заданное число.
Для выполнения данной операции в Python можно использовать цикл или генератор списка.
Пример кода:
def scalar_multiply(vector, scalar):
return [scalar * element for element in vector]В данном примере функция scalar_multiply принимает два аргумента: vector - вектор, представленный списком, и scalar - число для умножения. Функция возвращает новый вектор, полученный путем умножения каждого элемента исходного вектора на заданное число.
Пример использования:
vector = [1, 2, 3, 4, 5]
scalar = 2
result = scalar_multiply(vector, scalar)
print(result)В результате выполнения данного кода будет выведен новый вектор, полученный путем умножения каждого элемента исходного вектора на число 2: [2, 4, 6, 8, 10].
Произведение вектора на число широко применяется в различных областях, таких как машинное обучение, статистика, физика и другие. Например, в машинном обучении можно использовать это произведение для масштабирования признаков или весов модели.
В Python произведение вектора на число реализуется просто и эффективно с помощью списков и циклов. Эта операция является основой многих других операций в линейной алгебре, поэтому понимание ее принципов и умение ее применять является необходимым навыком для работы с векторами и матрицами.
Примеры использования произведения вектора на число в Python
Пример 1:
vec = [1, 2, 3]
k = 2
result = [k * x for x in vec]
print(result)
[2, 4, 6]
Пример 2:
vec = [5, -2, 0.5]
k = -3
result = [k * x for x in vec]
print(result)
[-15, 6, -1.5]
Пример 3:
vec = [0, 0, 0]
k = 10
result = [k * x for x in vec]
print(result)
[0, 0, 0]
Пример 4:
vec = [1, 1, 1, 1, 1]
k = 0
result = [k * x for x in vec]
print(result)
[0, 0, 0, 0, 0]
Пример 5:
vec = []
k = 5
result = [k * x for x in vec]
print(result)
[]
В приведенных примерах показано произведение вектора на число в Python. Операция выполняется с использованием генератора списка и умножения каждого элемента вектора на заданное число. Результирующий список содержит результаты произведения.
Вычисление произведения вектора на число в Python: алгоритм и примеры кода

Алгоритм вычисления произведения вектора на число в Python:
- Создать пустой массив для хранения результата.
- Пройтись по каждому элементу вектора.
- Умножить каждый элемент на заданное число.
- Добавить умноженный элемент в результирующий массив.
Пример кода:
def multiply_vector_by_scalar(vector, scalar):
result = []
for element in vector:
result.append(element * scalar)
return result
# Пример использования функции
vector = [1, 2, 3, 4, 5]
scalar = 2
result = multiply_vector_by_scalar(vector, scalar)
В данном примере мы создаем функцию "multiply_vector_by_scalar", которая принимает два аргумента: вектор и число. Функция проходит по каждому элементу вектора и умножает его на заданное число. Результатом работы функции является новый вектор, содержащий умноженные элементы.
Таким образом, вычисление произведения вектора на число в Python – это простой процесс, который может быть реализован с помощью небольшого алгоритма и функции.
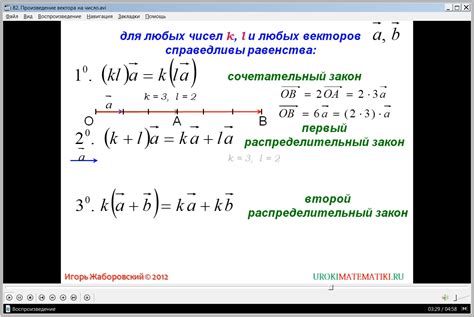
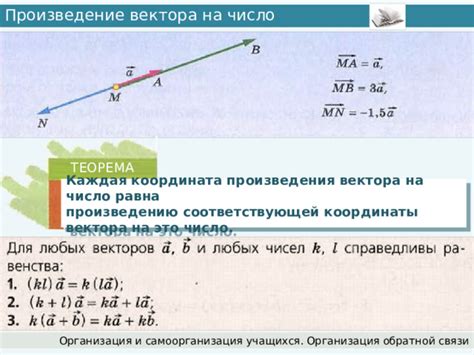
Произведение вектора на число и его свойства

Операция умножения вектора на число представляет собой действие, при котором каждая координата вектора умножается на это число. В Python для выполнения этой операции используется умножение вектора на число с помощью оператора *.
У произведения вектора на число есть несколько свойств, которые стоит учитывать:
Свойство
Формула
Описание
Ассоциативность
(r * s) * v = r * (s * v)
Порядок выполнения операций не влияет на результат
Дистрибутивность относительно сложения векторов
(r + s) * v = r * v + s * v
Умножение суммы векторов на число равно сумме умножений каждого вектора на это число
Дистрибутивность относительно сложения чисел
r * (v + w) = r * v + r * w
Умножение вектора на сумму чисел равно сумме умножений вектора на каждое число
Умножение на 1
1 * v = v
Умножение вектора на 1 не меняет его значения
Произведение вектора на число часто используется для масштабирования векторов, изменения их направления или изменения их длины.
Пример кода, демонстрирующий умножение вектора на число:
v = [2, 4, 6]
r = 2
result = [r * element for element in v]
В данном примере вектор v умножается на число r, и результатом является новый вектор result, каждая координата которого увеличивается в два раза.
Расширенные возможности произведения вектора на число в Python

Расширение на матрицы:
Вектор можно рассматривать как одномерную матрицу, и на него можно применять операции, которые обычно выполняются с матрицами. Например, можно умножать вектор на матрицу или матрицу на вектор.
Векторные операции:
Python предлагает удобные функции для выполнения различных векторных операций, таких как скалярное произведение, векторное произведение, сумма векторов и другие. Эти операции могут быть полезными при работе с произведением вектора на число.
Графические возможности:
Python имеет широкие возможности для графического представления векторов и их произведений. Библиотеки, такие как Matplotlib, позволяют создавать и отображать векторы и результаты их произведения в виде графиков и диаграмм. Это может быть полезным инструментом при визуализации и анализе данных.
Применение произведения вектора на число в реальных задачах

Применение произведения вектора на число в реальных задачах позволяет решать множество задач в различных областях, таких как физика, экономика, компьютерная графика и другие.
В физике произведение вектора на число используется, например, для определения силы, действующей на объект. При умножении вектора силы на число мы можем изменить его магнитуду и направление, что позволяет моделировать различные воздействия.
В экономике произведение вектора на число может быть применено для рассмотрения изменений в экономических показателях. Например, умножение вектора спроса на число позволяет анализировать влияние изменения цены на товары и услуги.
В компьютерной графике произведение вектора на число используется для изменения размеров и положения объектов. Путем умножения вектора, задающего положение объекта, на число, можно изменить его размер, повернуть или переместить его в пространстве.
Применение произведения вектора на число имеет многообразные практические применения и является важным инструментом в анализе и моделировании различных систем.