Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой. При изучении геометрии и решении задач, связанных с треугольниками, часто бывает нужно определить, является ли заданный треугольник равнобедренным. Этого можно достичь, зная значения сторон треугольника и применив определенные правила и формулы.
Существует несколько способов определить, является ли треугольник равнобедренным. Один из самых простых и известных – это сравнить длины сторон треугольника. Если две стороны равны между собой, то треугольник является равнобедренным.
Для определения равнобедренности треугольника по сторонам необходимо знать значения сторон. Для этого можно использовать известные геометрические формулы, применяя которые можно вычислить длины отрезков. После вычисления необходимо сравнить полученные значения, и если две стороны равны, то треугольник является равнобедренным.
Что это за равнобедренный треугольник?

В равнобедренном треугольнике есть несколько особенностей:
- Углы при основании равны;
- Основание делит треугольник на два равногранных треугольника;
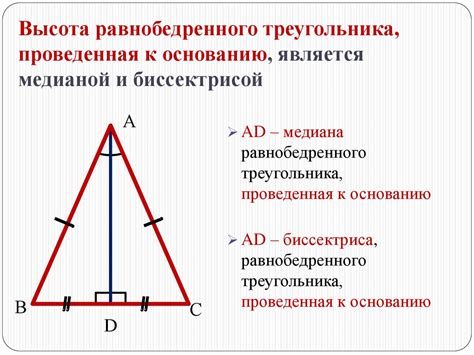
- Высота, проведенная из вершины угла при основании, является медианой и биссектрисой одновременно.
Равнобедренные треугольники появляются при решении различных геометрических задач и находят применение в различных областях науки и техники.
Запомните, что треугольник с двумя равными сторонами не всегда является равнобедренным треугольником. Для определения равнобедренности необходимо убедиться, что углы при основании также равны между собой.
Описание равнобедренного треугольника
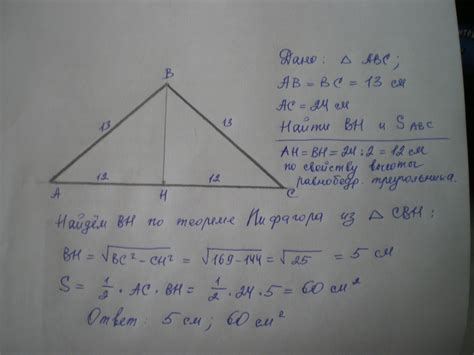
В равнобедренном треугольнике можно выделить несколько свойств:
- Биссектрисы основания равнобедренного треугольника являются высотами.
- Медиана, проведенная из вершины равнобедренного треугольника к основанию, является биссектрисой и медианой одновременно.
- Радиусы вписанной и описанной окружностей равнобедренного треугольника равны.
Равнобедренные треугольники могут быть как прямоугольными, так и непрямоугольными. В прямоугольном равнобедренном треугольнике, один из углов при основании является прямым углом.
Для определения равнобедренного треугольника по сторонам необходимо проверить, равны ли две из трех сторон. Если две стороны равны, то треугольник является равнобедренным.
Особенности равнобедренного треугольника
Все равнобедренные треугольники имеют следующие особенности:
| 1. | У них две стороны равны между собой. |
| 2. | Углы, противолежащие равным сторонам, также равны между собой. |
| 3. | Биссектриса угла, противолежащего равным сторонам, является высотой и медианой. |
Определить, является ли треугольник равнобедренным, можно сравнивая длины его сторон. Если две стороны равны между собой, то треугольник является равнобедренным.
Равнобедренные треугольники часто встречаются в геометрии и имеют свои приложения в различных областях науки и техники.
Как вычислить углы равнобедренного треугольника?

Для вычисления углов равнобедренного треугольника можно воспользоваться теоремой косинусов. Согласно этой теореме, квадрат одной стороны равнобедренного треугольника равен сумме квадратов двух других сторон, умноженной на два и умноженной на косинус угла между этими сторонами. Таким образом, зная длины сторон, можно вычислить косинусы углов.
Используя формулу для вычисления косинуса угла, можно найти значение косинуса угла, затем вычислить сам угол, используя обратную функцию косинуса. В результате получим значения для всех углов равнобедренного треугольника.
Углы равнобедренного треугольника могут быть найдены с использованием тригонометрических функций и математических формул, что позволяет получить точное значение для каждого угла.
Как вычислить площадь равнобедренного треугольника?
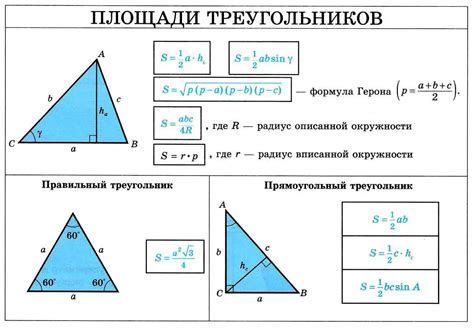
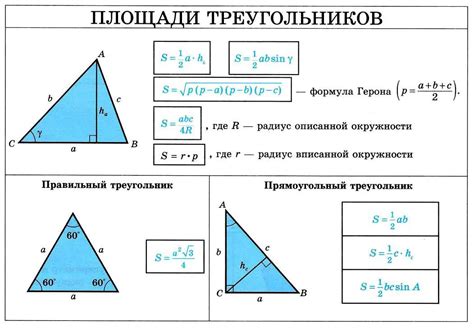
Площадь равнобедренного треугольника можно вычислить по формуле, используя длины его сторон.
Шаг 1: Определите длину основания треугольника. Основание – это одна из двух равных сторон треугольника.
Шаг 2: Определите длину высоты треугольника. Высота треугольника – это перпендикуляр, опущенный из вершины треугольника на основание.
Шаг 3: Вычислите площадь треугольника, умножив половину основания на высоту треугольника.
Формула для вычисления площади равнобедренного треугольника:
Площадь = (0.5 * основание) * высота
Например, если длина основания равна 6 единицам, а длина высоты равна 4 единицам, то площадь равнобедренного треугольника будет:
Площадь = (0.5 * 6) * 4 = 12 единиц²
Таким образом, площадь равнобедренного треугольника с основанием 6 единиц и высотой 4 единицы составляет 12 единиц².
Формулы для нахождения сторон равнобедренного треугольника
В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона может быть разной. Чтобы найти длины сторон равнобедренного треугольника, можно использовать следующие формулы:
1. Формула для нахождения длины основания треугольника:
основание = (периметр - 2 * равные стороны) / 2
2. Формула для нахождения длины равных сторон треугольника:
равные стороны = (периметр - основание) / 2
Здесь периметр треугольника – это сумма длин всех его сторон.
Найдя длину одной из равных сторон и основания, можно легко определить стороны равнобедренного треугольника, исходя из них. Причем, любая из равных сторон может считаться основанием, в зависимости от того, какая из сторон известна.
Примечание: Для использования данных формул необходимо знать значение периметра и одной из сторон треугольника.
Как построить равнобедренный треугольник?

Если у вас есть стороны AB и AC, и угол между ними равен α, вы можете построить равнобедренный треугольник следующим образом:
| Шаг | Действие |
|---|---|
| 1 | Нарисуйте отрезок BC так, чтобы AB = AC и угол BAC = α. |
| 2 | Проведите отрезок BA и отрезок CA. |
Получившийся треугольник ABC будет равнобедренным, так как стороны AB и AC равны между собой.
Теперь вы знаете, как построить равнобедренный треугольник по заданным сторонам и углу между ними. Пользуйтесь этим знанием для решения геометрических задач или для конструирования различных фигур.
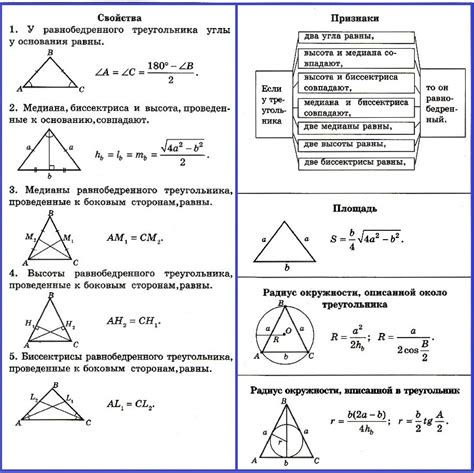
Свойства равнобедренного треугольника
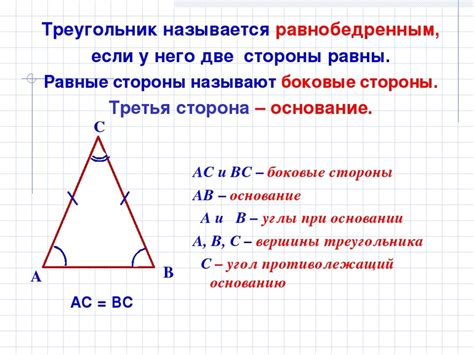
Свойства равнобедренного треугольника:
- У равнобедренного треугольника две стороны равны друг другу. Это означает, что две стороны, выходящие из вершины основания, имеют одинаковую длину.
- Основание треугольника делит его высоту на две равные части.
- Равнобедренный треугольник имеет два равных угла, которые находятся против равных сторон.
- Средняя линия равнобедренного треугольника – линия, соединяющая середины боковых сторон, равна половине основания треугольника.
- Центр окружности, вписанной в равнобедренный треугольник, лежит на оси симметрии треугольника, а расстояние от вершины основания до центра окружности равно расстоянию от этой вершины до боковой стороны треугольника.
Знание свойств равнобедренного треугольника позволяет легко определить его по данным о сторонах и углам, а также упрощает решение задач, связанных с равнобедренными треугольниками.
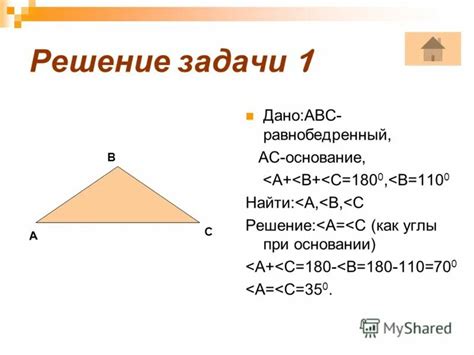
Примеры решения задач на равнобедренные треугольники
Решение задач на равнобедренные треугольники может быть полезно при изучении геометрии и решении геометрических задач. Для определения равнобедренного треугольника необходимо использовать определение этого понятия и применять формулы для расчёта длин сторон и углов треугольника.
Пример 1:
Дан треугольник ABC со сторонами AB = 5, BC = 4 и AC = 5. Найдите углы треугольника и определите, является ли он равнобедренным.
Решение:
Для нахождения углов треугольника можно использовать теорему косинусов. По этой теореме можно выразить угол через длины сторон треугольника.
Угол BAC можно найти по формуле:
cos(A) = (b^2 + c^2 - a^2) / (2*b*c)
Подставим данные и решим уравнение:
cos(A) = (4^2 + 5^2 - 5^2) / (2*4*5) = (16 + 25 - 25) / 40 = 16 / 40 = 0.4
Находим угол A через арккосинус:
A = arccos(0.4) ≈ 66.4°
Аналогично находим остальные углы:
B ≈ 44.6°
C ≈ 69°
Поскольку все углы треугольника ABC не равны, треугольник не является равнобедренным.
Пример 2:
Дан равнобедренный треугольник DEF с основанием EF = 6 и боковыми сторонами DE = DF = 5. Найдите углы треугольника.
Решение:
Поскольку треугольник DEF является равнобедренным, то его два боковых угла DEF и DFE равны между собой. Третий угол EFD можно найти, зная сумму углов треугольника (180°).
Углы DEF и DFE можно найти, используя определение равнобедренного треугольника:
DEF = DFE = (180° - EFD) / 2
Подставим данное значение:
5 = (180° - EFD) / 2
Решим уравнение:
180° - EFD = 2 * 5
EFD = 180° - 10 = 170°
Находим углы DEF и DFE:
DEF = DFE = (180° - 170°) / 2 = 5°
Таким образом, углы треугольника DEF равны 5°, 5° и 170°.
Приведённые примеры демонстрируют основные приёмы решения задач на равнобедренные треугольники. Вам рекомендуется самостоятельно решить несколько задач, чтобы лучше понять и применить эти приёмы.
Задачи для самопроверки на равнобедренный треугольник
Для самостоятельной проверки и закрепления знаний о равнобедренных треугольниках, решите следующие задачи:
- Найдите все равнобедренные треугольники с периметром 12, если известно, что все стороны треугольника – целочисленные значения.
- В треугольнике с углами 30°, 100° и 50°, найдите длину основания и высоту, если сторона равна 8.
- Проверьте, является ли треугольник со сторонами 5, 5 и 8 равнобедренным. Если да, то найдите площадь этого треугольника.
- Найдите периметр и площадь равнобедренного треугольника, если катеты равны 6 и гипотенуза равна 8.
- Проверьте, является ли треугольник со сторонами 7, 7 и 10 равнобедренным. Если да, то найдите площадь этого треугольника.
Попробуйте решить задачи самостоятельно. После окончания решения проверьте свои ответы. Если возникли затруднения, обратитесь к теоретическому материалу или попросите помощи у преподавателя.