Определение размера матрицы — простые способы и советы для быстрого расчета

Матрицы - одна из основных концепций линейной алгебры, применяемых в различных областях науки и техники. Знание размера матрицы является ключевым элементом при выполнении операций с ней. Определить размер матрицы можно несколькими простыми способами, которые обязательно стоит запомнить.

Первый и наиболее простой способ - посчитать количество строк и столбцов в матрице. Для этого нужно обратить внимание на свойства самой матрицы. В матрице размером m на n (m - количество строк, n - количество столбцов) будет ровно m строк и n столбцов. Это правило основывается на строении матрицы и дает наиболее точный результат.

Если желаемая матрица записана в виде линейного массива, то для определения ее размера можно воспользоваться другим трюком. Найдите количество элементов в массиве и разделите его на желаемый размер строки матрицы. Если количество элементов делится на размер строки без остатка, то это возможный размер матрицы. Просто примечательно, что для этого способа не требуется рассматривать саму структуру матрицы - достаточно знать количество элементов.

Важно помнить, что размеры матрицы могут быть одинаковыми только если количество строк и столбцов равны. Всегда проверяйте правила и особенности, связанные с работой с матрицами, чтобы избежать ошибок и получить точный результат.

Правила определения размера матрицы

Определение размера матрицы представляет собой важный шаг в решении различных задач, связанных с линейной алгеброй и математикой в целом. Существует несколько правил, которые помогают определить размеры матрицы.

Правило 1: Размер матрицы определяется числом строк и числом столбцов: m x n, где m - число строк, n - число столбцов.

Правило 2: Для определения размеров матрицы можно воспользоваться формулой: m = max(r₁, r₂, ..., r_k) и n = max(c₁, c₂, ..., c_k), где r_i - число элементов в i-й строке, c_i - число элементов в i-м столбце, k - количество строк/столбцов.

Правило 3: Чтобы определить размеры матрицы, можно также посчитать количество элементов в каждой строке и каждом столбце. Если число элементов в каждой строке одинаково, и число элементов в каждом столбце одинаково, то размеры матрицы будут m x n.

Правило 4: Если задана матрица в виде списков или массивов, размеры матрицы можно определить, посчитав количество строк и количество столбцов в заданной структуре данных.

Используя эти простые правила, вы сможете быстро и точно определить размеры матрицы, что поможет вам дальше работать с ней и решать различные задачи в области линейной алгебры.

Определение размера матрицы с помощью техники размерности

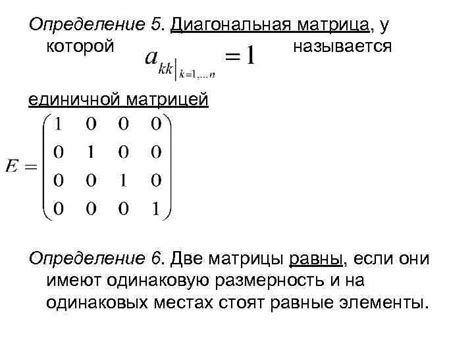
Для определения числа строк можно использовать функцию len(), которая возвращает длину списка. Если каждая строка матрицы представляет собой отдельный список, то длина такого списка будет равна количеству строк матрицы.

Например, для матрицы:

matrix = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]

Мы можем определить количество строк следующим образом:

num_rows = len(matrix)

Чтобы определить количество столбцов, можно использовать функцию len() для любой строки в матрице, так как все строки имеют одинаковую длину.

Например, для матрицы выше, мы можем определить количество столбцов следующим образом:

num_columns = len(matrix[0])

Итак, размер матрицы составляет num_rows строк на num_columns столбцов.

Техника размерности является универсальным способом определения размера матрицы и может быть использована для матриц любого размера.

Пример применения:

matrix = [[1, 2],
[3, 4],
[5, 6]]
num_rows = len(matrix)
num_columns = len(matrix[0])
print("Размер матрицы:", num_rows, "x", num_columns)

Размер матрицы: 3 x 2

Определение размера матрицы используя правило определителя

Одним из способов определения размера матрицы является использование правила определителя. Правило гласит, что определитель квадратной матрицы равен произведению элементов ее главной диагонали.

Для применения этого правила к прямоугольным матрицам, необходимо привести их к квадратному виду путем добавления нулевых строк или столбцов. Затем применить правило определителя к полученной квадратной матрице.

Проиллюстрируем этот способ на примере матрицы:

1 2 3
4 5 6

Добавим нулевую строку:

1 2 3
4 5 6
0 0 0

Теперь применим правило определителя:

det(A) = (1 * 5 * 0) + (2 * 6 * 0) + (3 * 4 * 0) - (3 * 5 * 0) - (2 * 4 * 0) - (1 * 6 * 0)

det(A) = 0

Таким образом, размер исходной матрицы равен 2x3.

Использование правила определителя позволяет определить размер матрицы без необходимости подсчета количества строк и столбцов вручную. Этот метод особенно полезен при работе с большими матрицами.

Обратите внимание, что данное правило применимо только к квадратным матрицам и прямоугольные матрицы нужно приводить к квадратному виду.